题目

Description
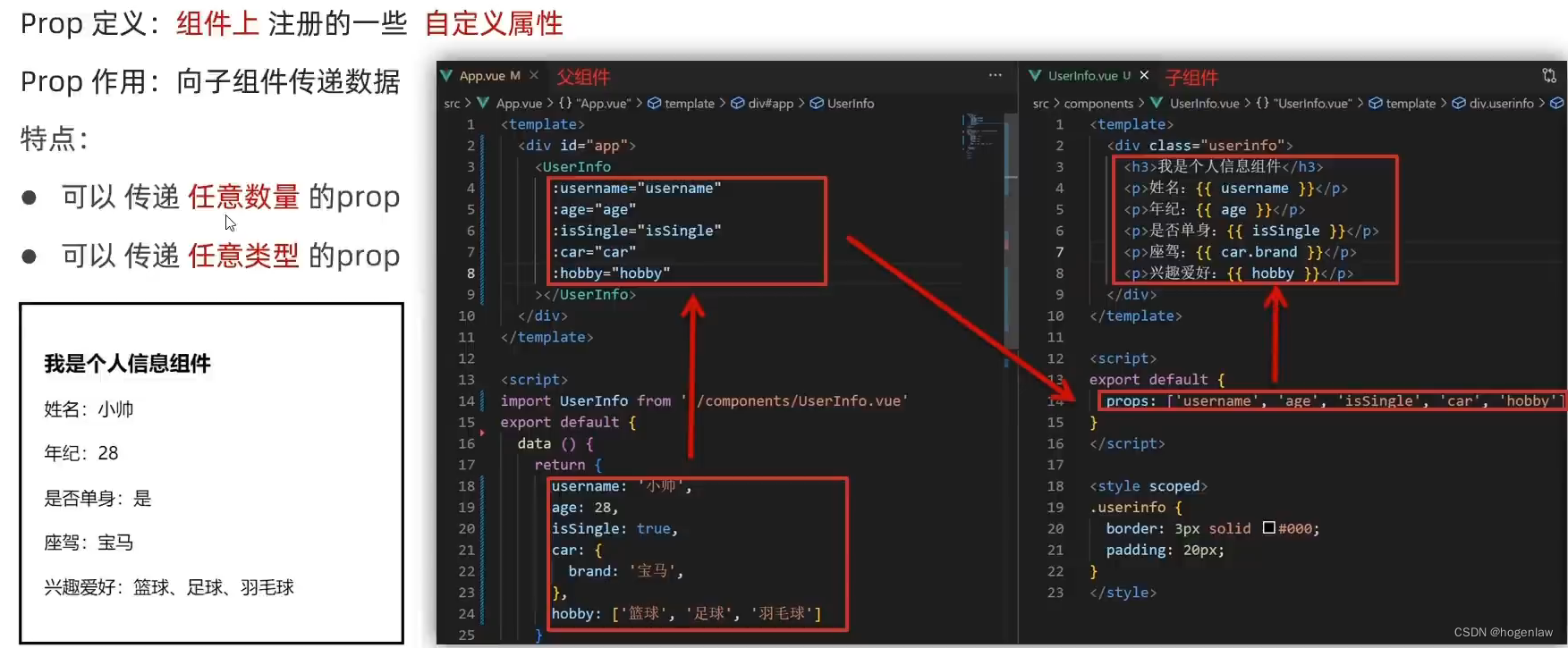
数独是一个基于逻辑的组合数字放置拼图，在世界各地都很受欢迎。
在这个问题上，让我们关注  网格的拼图，其中包含  个区域。 目标是用十六进制数字填充整个网格，即 ，以便每列，每行和每个区域包含所有十六进制数字。
下图显示了一个被成功解决的数独例子：

昨天，周老师解决了一个数独并将其留在桌面上。 然而，龙龙想和他开个玩笑——龙龙打算对这个已经解决的数独进行多次以下操作。
 选择一个   的小区域并顺时针旋转  度。
周老师回来发现他拼好的数独板被打乱了，开始挠头，你能帮他以最小的步数恢复原样吗？请你手把手的教他怎么做，也就是需要输出方案。
请注意选择要旋转的方块不能跨越任何小区域，也就是说必须选择一块完整的小区域旋转。小区域的定义在上面， 的网格被分成  个小区域。
Input
第一行输入一个正整数  表示数据组数；
接下来每组数据输入一个  的数独图，表示被龙龙打乱后的数独面板。
Output
对于每组数据：
第一行输出一个整数  ，表示周老师最少需要逆时针旋转多少次才能恢复原样。
接下来输出  行，每行两个数，表示逆时针旋转一次第行第列的小矩阵。

---

C++完整代码（含详细注释）

有查重！！记得修改呀

#include <iostream>
#include <vector>
#include <cstring>
#include <climits>
using namespace std;

const int N = 16; // 数独面板的大小
int sudoku[N][N]; // 数独面板
int rowCheck[N][N+1]; // 每行数字的出现情况
int colCheck[N][N+1]; // 每列数字的出现情况

struct Node
{
    int x, y, t; // 旋转的位置和次数
};

int minRotations; // 最小旋转次数
vector<Node> curRotation; // 当前旋转方案
vector<Node> minRotation; // 最小旋转方案


// 将小区域逆时针旋转90度
void rotateCounterClockwise(int x, int y) {
    x *= 4; // 将坐标转换成小区域内的坐标
    y *= 4;
    for (int i = 0; i < 2; i++) {
        for (int j = i; j < 3 - i; j++) {
            int temp = sudoku[x + i][y + j];
            sudoku[x + i][y + j] = sudoku[x + j][y + 3 - i];
            sudoku[x + j][y + 3 - i] = sudoku[x + 3 - i][y + 3 - j];
            sudoku[x + 3 - i][y + 3 - j] = sudoku[x + 3 - j][y + i];
            sudoku[x + 3 - j][y + i] = temp;
        }
    }
}


// 检查旋转后的小区域是否合法
bool isValidRotation(int x, int y) {
    x *= 4; // 将坐标转换成小区域内的坐标
    y *= 4;
    for (int i = x; i <= x + 3; i++) {
        for (int j = y; j <= y + 3; j++) {
            int num = sudoku[i][j];
            if (rowCheck[i][num] || colCheck[j][num]) {
                return false;
            }
        }
    }
    // 更新每行和每列数字的出现情况
    for (int i = x; i <= x + 3; i++) {
        for (int j = y; j <= y + 3; j++) {
            int num = sudoku[i][j];
            rowCheck[i][num] = true;
            colCheck[j][num] = true;
        }
    }
    return true;
}

// 撤销旋转操作
void undoRotation(int x, int y) {
     x *= 4; // 将坐标转换成小区域内的坐标
     y *= 4;
    for (int i = x; i < x + 4; i++) {
        for (int j = y; j < y + 4; j++) {
            int num = sudoku[i][j];
            rowCheck[i][num] = false;
            colCheck[j][num] = false;
        }
    }
}

// 深度优先搜索，尝试不同的旋转方案
void dfs(int x, int y, int count) {
    if (x == 4) { // 如果已经遍历完所有小区域
        if (count < minRotations) { // 更新最小旋转次数和旋转方案
            minRotations = count;
            minRotation = curRotation;
        }
        return;
    }

    for (int op = 0; op < 4; op++) { // 尝试不同的旋转次数
        if (!isValidRotation(x, y)) { // 如果旋转后的小区域不合法，继续进行逆时针旋转
            rotateCounterClockwise(x, y);
            continue;
        }

        curRotation.push_back(Node{ x + 1, y + 1, op }); // 将当前旋转方案加入当前旋转方案列表

        if (y == 3) { // 如果已经遍历完当前行的所有小区域，进入下一行
            dfs(x + 1, 0, count + op);
        }
        else dfs(x, y + 1, count + op); // 继续遍历当前行的下一个小区域

        curRotation.pop_back(); // 撤销当前旋转方案
        undoRotation(x, y); // 撤销旋转操作
        rotateCounterClockwise(x, y); // 还原小区域
    }
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        minRotations = INT_MAX;
        curRotation.clear();
        minRotation.clear();
        memset(colCheck, 0, sizeof colCheck);
        memset(rowCheck, 0, sizeof rowCheck);

        // 读入数独面板
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++) {
                char hex;
                cin >> hex;
                int dec = stoi(string(1, hex), nullptr, 16);
                sudoku[i][j] = dec;
            }
        }

        dfs(0, 0, 0); // 开始深度优先搜索
        cout << minRotations << endl; // 输出最小旋转次数
        for (auto& per : minRotation) { // 输出最小旋转方案
            for (int i = 0; i < per.t; i++) {
                cout << per.x << " " << per.y << endl;         
            }
        }
    }
    return 0;
}