文章目录
- 竞赛链接
- Q1:7021. 判断通过操作能否让字符串相等 I
- Q2:7005. 判断通过操作能否让字符串相等 II(贪心)
- Q3:2841. 几乎唯一子数组的最大和
- 竞赛时代码——滑动窗口
- Q4:8050. 统计一个字符串的 k 子序列美丽值最大的数目(贪心+计数+组合数学)
- 竞赛时代码(赛时通过,结束之后被rejudge了)🤯
- 正确解法⭐
- 成绩记录
竞赛链接
https://leetcode.cn/contest/biweekly-contest-112/
Q1:7021. 判断通过操作能否让字符串相等 I
https://leetcode.cn/problems/check-if-strings-can-be-made-equal-with-operations-i/
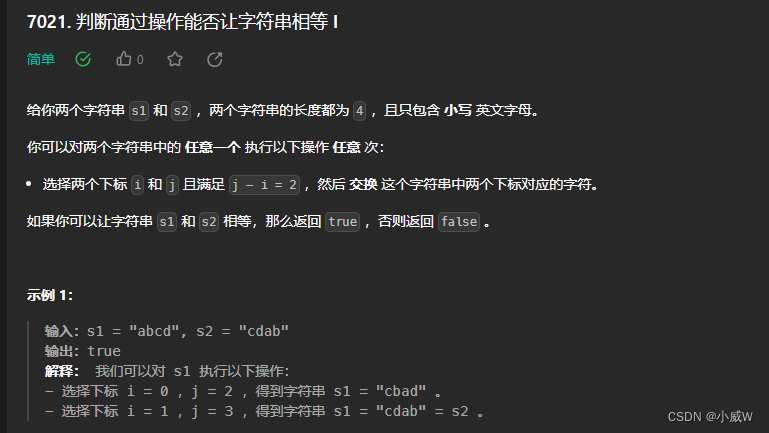
提示:
s1.length == s2.length == 4
s1 和 s2 只包含小写英文字母。
class Solution {
public boolean canBeEqual(String s1, String s2) {
// 取出各个字符
char a = s1.charAt(0), b = s1.charAt(1), c = s1.charAt(2), d = s1.charAt(3);
char a2 = s2.charAt(0), b2 = s2.charAt(1), c2 = s2.charAt(2), d2 = s2.charAt(3);
// 比较
return (a == a2 || a == c2) && (a + c == a2 + c2) && (b == b2 || b == d2) && (b + d == b2 + d2);
}
}
Q2:7005. 判断通过操作能否让字符串相等 II(贪心)
https://leetcode.cn/problems/check-if-strings-can-be-made-equal-with-operations-ii/description/
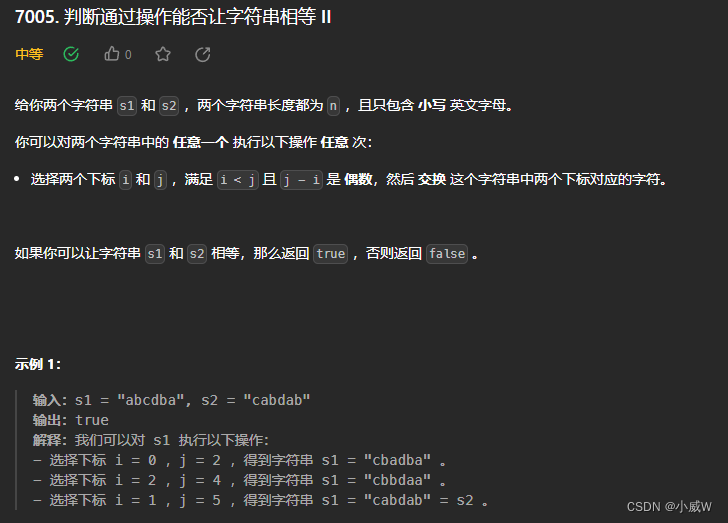
提示:
n == s1.length == s2.length
1 <= n <= 10^5
s1 和 s2 只包含小写英文字母。
只要两个字符串的奇偶位的各个字符的数量相等,就一定可以通过交换位置换成相同的字符串。
class Solution {
public boolean checkStrings(String s1, String s2) {
// 分别记录两个字符串的奇偶位字符数量
int[] cnt1 = new int[26], cnt2 = new int[26], cnt3 = new int[26], cnt4 = new int[26];
int n = s1.length();
for (int i = 0; i < n; ++i) {
if (i % 2 == 0) {
cnt1[s1.charAt(i) - 'a']++;
cnt3[s2.charAt(i) - 'a']++;
} else {
cnt2[s1.charAt(i) - 'a']++;
cnt4[s2.charAt(i) - 'a']++;
}
}
// 比较是否相等
return Arrays.equals(cnt1, cnt3) && Arrays.equals(cnt2, cnt4);
}
}
Q3:2841. 几乎唯一子数组的最大和
https://leetcode.cn/problems/maximum-sum-of-almost-unique-subarray/

提示:
1 <= nums.length <= 2 * 10^4
1 <= m <= k <= nums.length
1 <= nums[i] <= 10^9
竞赛时代码——滑动窗口
滑动窗口,维护窗口内的总和以及独特元素数量。
class Solution {
public long maxSum(List<Integer> nums, int m, int k) {
Map<Integer, Integer> cnt = new HashMap<>();
int n = nums.size();
long sum = 0, ans = 0;
// 双指针+滑动窗口
for (int i = 0, j = 0; i < n; ++i) {
// 加入元素
cnt.merge(nums.get(i), 1, Integer::sum);
sum += nums.get(i);
// 移除元素
if (i - j >= k) {
cnt.merge(nums.get(j), -1, Integer::sum);
sum -= nums.get(j);
if (cnt.get(nums.get(j)) == 0) cnt.remove(nums.get(j));
j++;
}
// 如果是几乎唯一子数组,就尝试更新答案
if (i - j + 1 == k && cnt.size() >= m) ans = Math.max(ans, sum);
}
return ans;
}
}
Q4:8050. 统计一个字符串的 k 子序列美丽值最大的数目(贪心+计数+组合数学)
https://leetcode.cn/problems/count-k-subsequences-of-a-string-with-maximum-beauty/
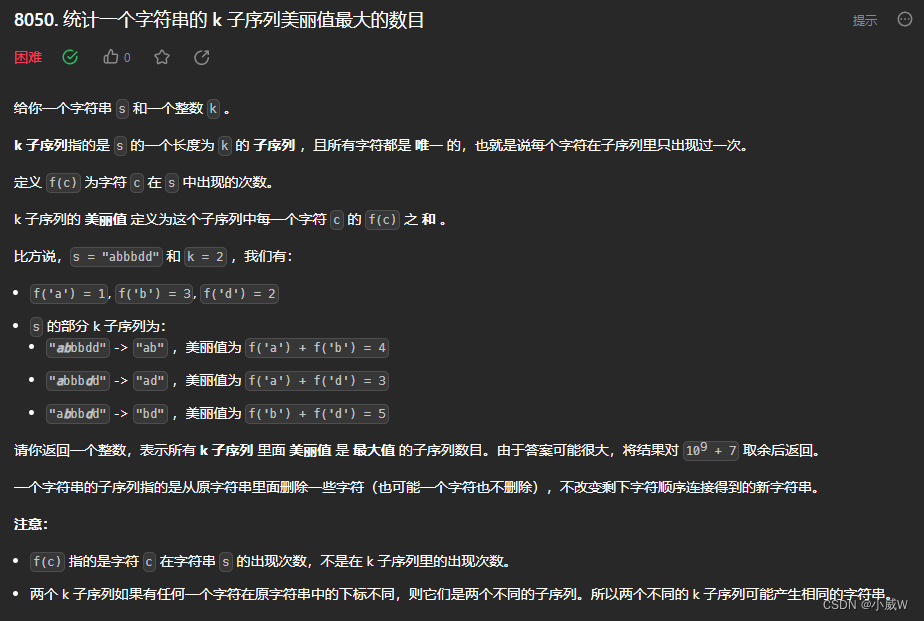
提示:
1 <= s.length <= 2 * 10^5
1 <= k <= s.length
s 只包含小写英文字母。
竞赛时代码(赛时通过,结束之后被rejudge了)🤯
贪心地选取出现次数最多的字符。
如果若干个字符的出现次数一样,那么就把答案乘上对应的组合数。
比如从 0,1,1,1,2,3 中取 k 为 4,那么 3 和 2 是一定要被选择的,然后在 3 个 1 中任意选择 2 个 1 即可。答案为 3 * 2 * 1 * C(3,2) = 18。
class Solution {
public int countKSubsequencesWithMaxBeauty(String s, int k) {
if (k > 26) return 0;
long[] cnt = new long[26]; // 记录各个字符的数量
for (char ch: s.toCharArray()) {
cnt[ch - 'a']++;
}
Arrays.sort(cnt); // 按字符数量排序
long ans = 1, MOD = (long)1e9 + 7;
long mn = cnt[26 - k]; // 可选择的出现次数最少的字符出现次数
ans = mn;
// 求组合数是几选几
int end = -1;
for (int i = 26 - k + 1; i < 26; ++i) {
if (cnt[i] != mn) {
if (end == -1) end = i;
}
ans = (ans * cnt[i]) % MOD;
}
if (end == -1) end = 26;
for (int i = 0; i < end; ++i) {
if (cnt[i] == mn) {
int x = end - i;
long y = op(x, k - 26 + end); // 求组合数
ans = (ans * y) % MOD;
break;
}
}
return (int)ans;
}
// 求组合数C(x, y)
public long op(int x, int y) {
long ans = 1, m = 1;
while (y != 0) {
ans *= x;
m *= y;
x--;
y--;
}
return ans / m;
}
}
错误的样例是
"xzkilqoqfdnjextrgqpywahbmsu"
23
预期结果是 132,但是我的代码返回了 0。
原因可能是因为没有考虑到 mn = 0,那后续怎么乘都还是 0。
正确解法⭐

这种做法的好处是枚举更清晰,代码逻辑也不会混乱。
Q:为什么 k 太大就不存在合法子序列?
A:因为 k 太大时,独特的字母的数量会不够用。
class Solution {
final long MOD = (long)1e9 + 7;
public int countKSubsequencesWithMaxBeauty(String s, int k) {
// 统计每种字符出现的次数
int[] cnt = new int[26];
for (char ch: s.toCharArray()) {
cnt[ch - 'a']++;
}
// 统计每种出现次数,以及多少种字符是这种次数
TreeMap<Integer, Integer> cc = new TreeMap<>();
for (int c: cnt) {
if (c > 0) cc.merge(c, 1, Integer::sum);
}
long ans = 1;
// .descendingMap()返回按键降序排序
for (Map.Entry<Integer, Integer> e: cc.descendingMap().entrySet()) {
int c = e.getKey(), num = e.getValue();
if (num >= k) {
// 乘上 c^k 和 C(num, k)
return (int) (ans * pow(c, k) % MOD * comb(num, k) % MOD);
}
ans = ans * pow(c, num) % MOD;
k -= num;
}
return 0; // k太大,没有那么多种字符
}
// 计算 x^n 快速幂
long pow(long x, int n) {
long res = 1;
// 把 n 看成二进制数字,哪些位置是 1,就把它乘起来就好了
for (; n > 0; n /= 2) {
if (n % 2 == 1) res = res * x % MOD;
x = x * x % MOD;
}
return res;
}
// 计算 C(n,k)
long comb(long n, long k) {
long res = n;
for (int i = 2; i <= k; ++i) {
res = res * --n / i;
}
return res % MOD;
}
}
关于快速幂可见:【算法基础:数学知识】4.4 快速幂
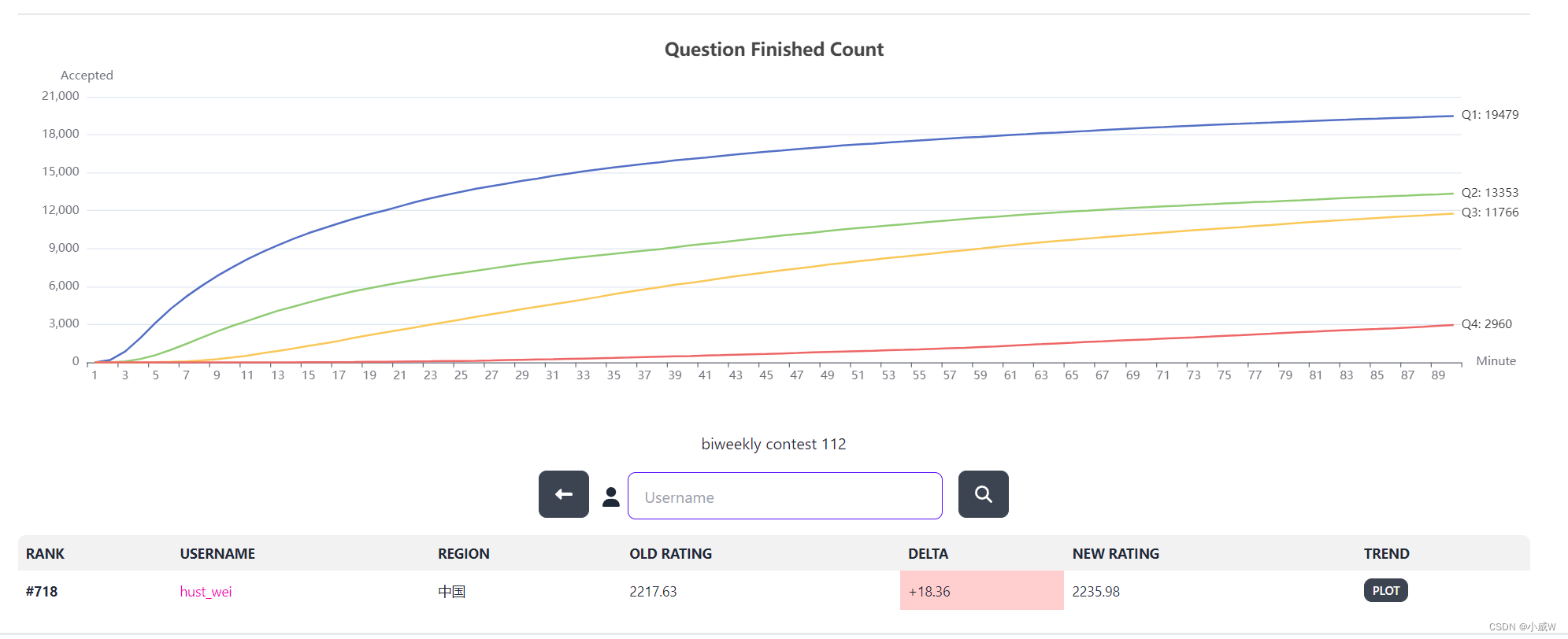
成绩记录

就,还好。
WA 次数有点多。