目录
摘要:
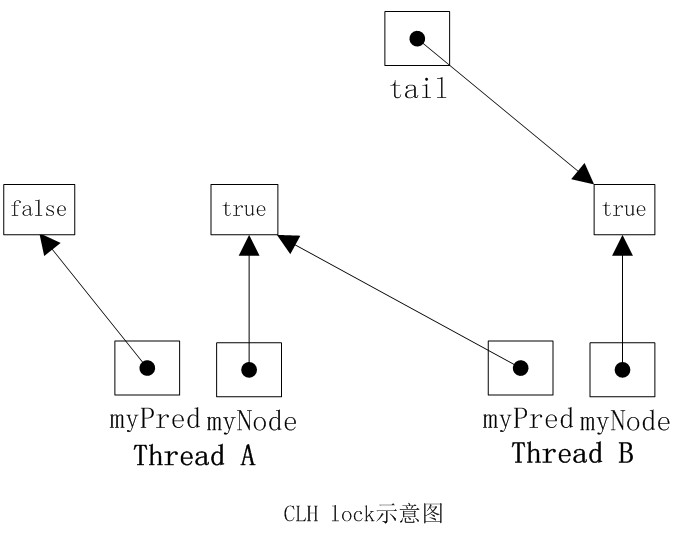
1.蝙蝠优化算法的基本原理:
2.蝙蝠优化算法的流程:
3.仿真实验分析:
摘要:
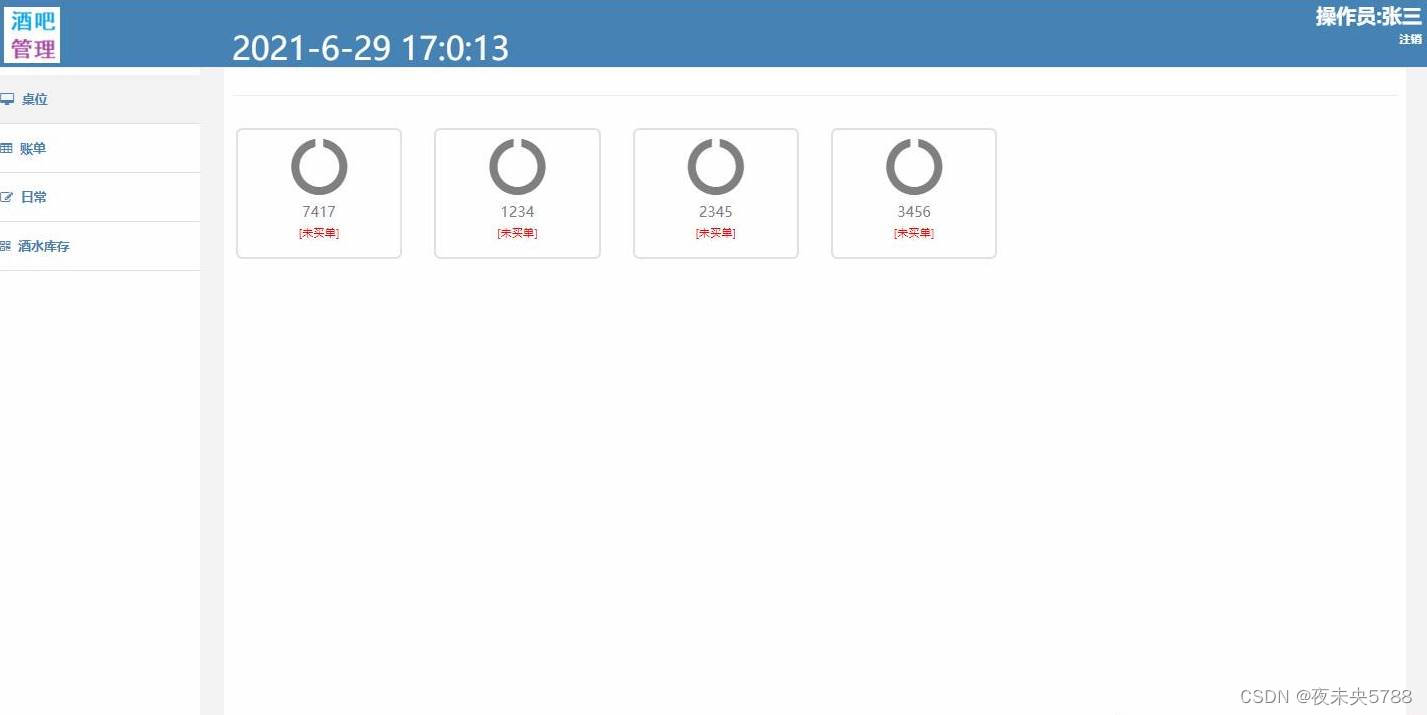
基于Matalb平台,构建基于蝙蝠活动行为的蝙蝠优化算法,对一个含有6个火电机组的电力系统进行优化调度,其中优化调度的目标函数为火电机组运行成本最小,其中约束条件有:功率平衡约束,火电机组最大最小出力约束,火电机组爬坡约束,网络潮流约束,等。结果表明,所提的蝙蝠优化算法可以很好的完成电力系统优化调度决策任务。程序注释详细,出图美观,适合初学者学习入门智能优化算法或电力系统经济调度。
1.蝙蝠优化算法的基本原理:
蝙蝠算法是模拟蝙蝠发出和接收自身发出的超声波来捕食猎物这一行为提出的一
种全局型群智能优化算法。在该算法中,每只蝙蝠在搜索空间中的位置代表一个解,对
于不同的适应度函数,每只蝙蝠都有自己的适应度值,算法比较每只蝙蝠的适应度值来
找出当前全局最优位置,然后调整蝙蝠种群的脉冲发射频率、强度,朝着当前最优位置
不断搜索,最终找到全局最优解。
(1) 种群中的所有蝙蝠都用回声定位系统来判断距离,并且它们能够区分猎物与障
碍物。
(2) 蝙蝠在位置Xi以速度Vi 飞行。以固定频率fmin,强度Ao来搜捕猎物,它们能够
根据与猎物的距离自发调节发出声波的波长或者频率,在接近猎物时自发调整脉冲发射
频率ri。
(3) 假设声波强度的最小值为Amin ,最大值为Ao 。 蝙蝠的捕食过程可描述为:蝙蝠种群随机分布在搜索空间中,每只蝙蝠的位置为Xi( 1, 2,3,..,N),蝙蝠能够在位置Xi发出频率为fi强度为Ao的超声波搜索猎物,确定目标后,蝙蝠以速度Vi 向猎物飞行。并根据猎物与自己的距离实时调整飞行速度、声波强度和脉冲发射频率,逐渐向猎物靠近,最终成功捕食猎物。根据蝙蝠捕食过程,算法的迭代次数为t,蝙蝠个体i 发出超声波的频率、速度和位置在第t 代的更新公式如下:
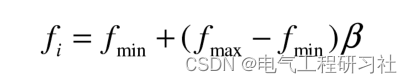 (2-1)
(2-1)
 (2-2、2-3)
(2-2、2-3)
当蝙蝠种群逐渐向全局最优解靠近时,算法就采用局部搜索策略,局部位置更新
公式如下:
 (2-4)
(2-4)
2.蝙蝠优化算法的流程:
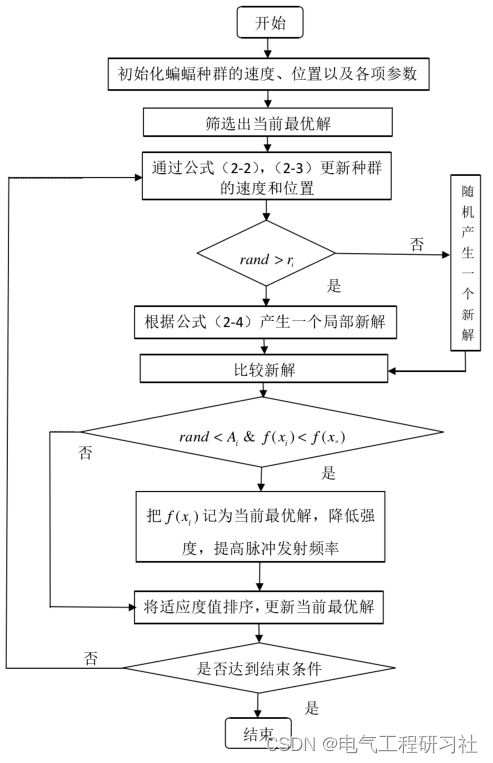
3.仿真实验分析:
以下为部分运行结果,主要是分为电力系统稳态运行情况下的和电力系统暂稳态运行情况下的:

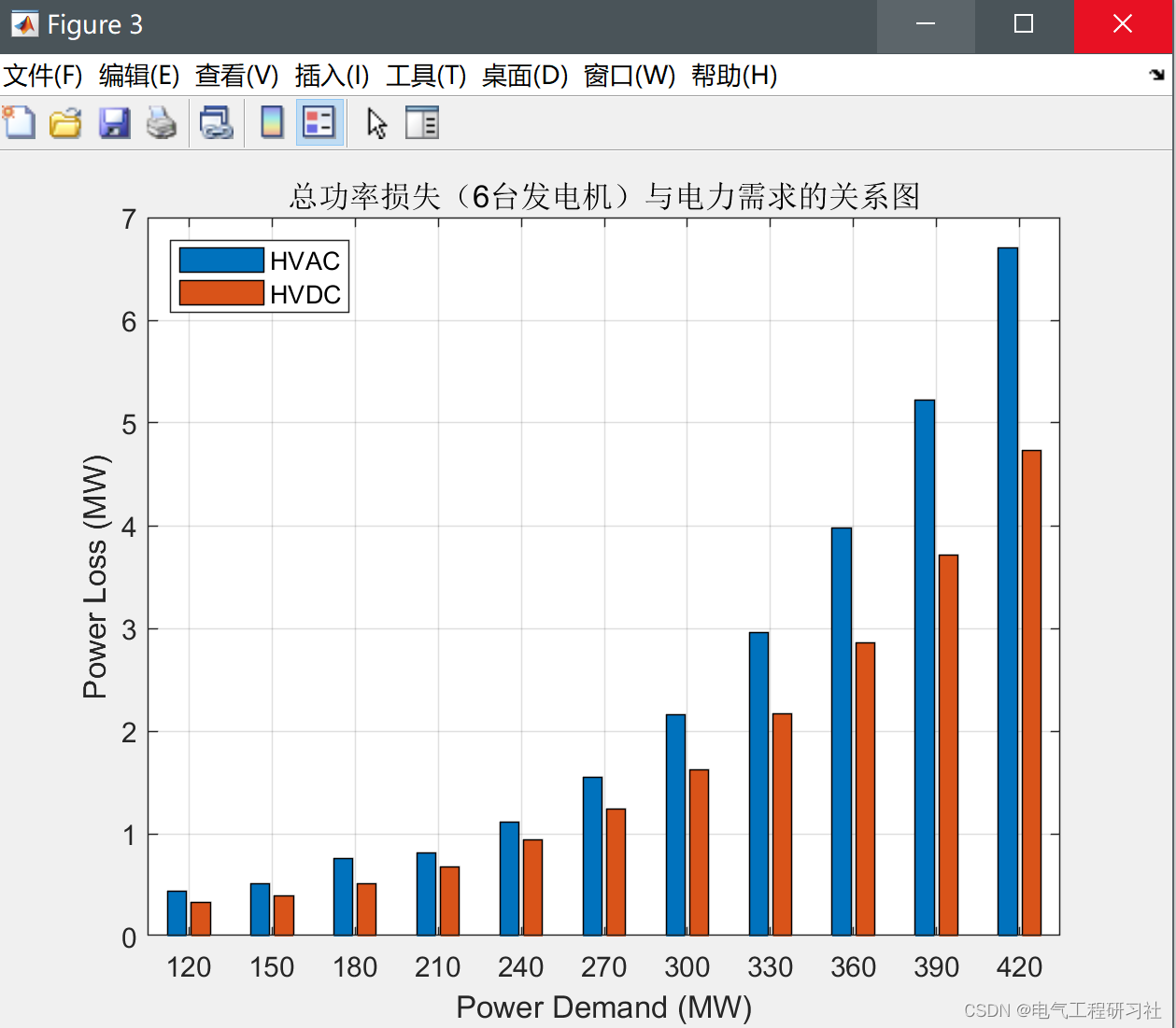

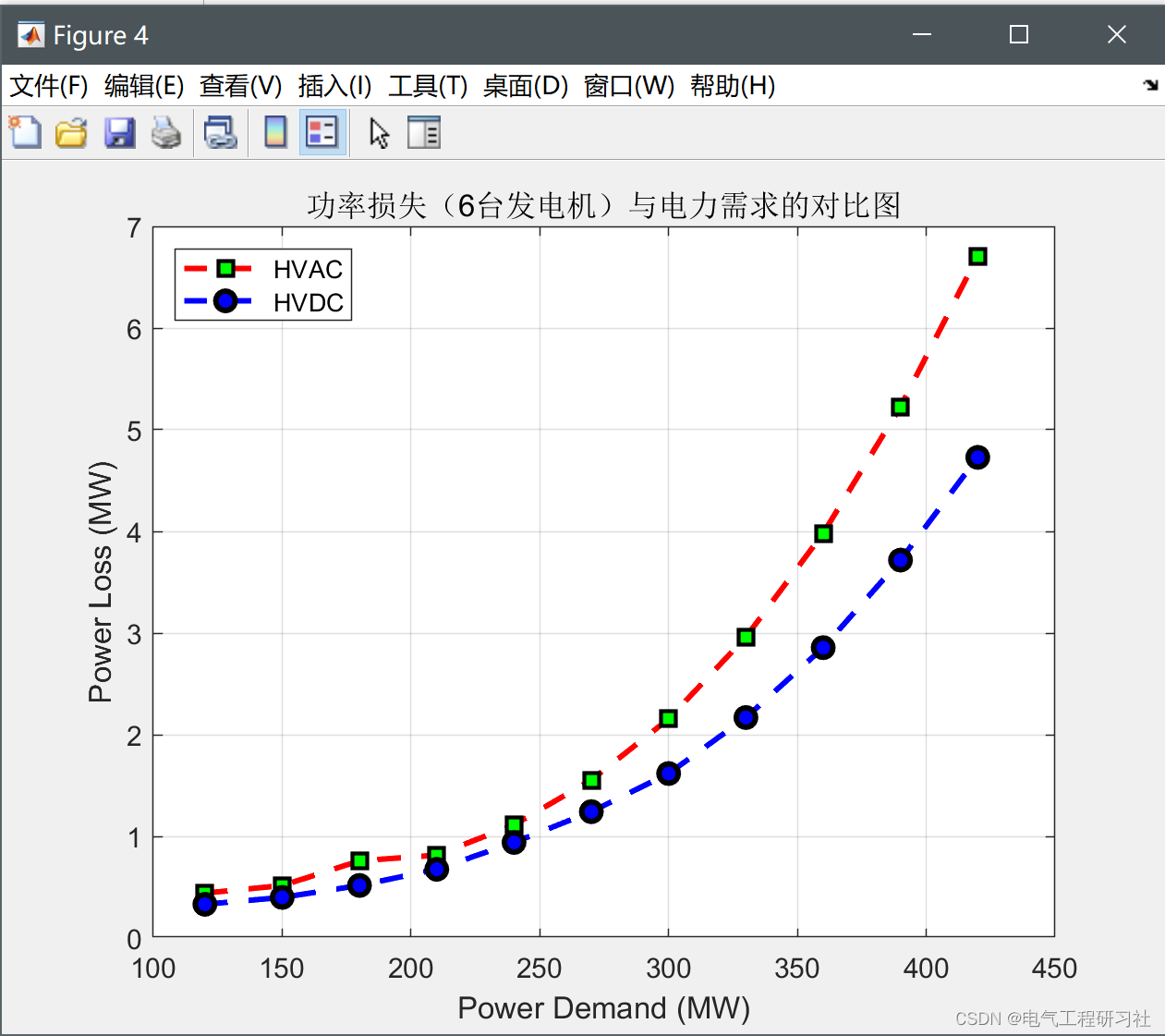
部分代码:
clc; % 清除命令窗口中的任何工作或数据
clear; % 在使用前清除所有可变量的值
close all; % 关闭所有打开的图片
%% 导入机组参数与模型
doc_name = 'ED_result.doc';
plot_Fcost = 'FuelCostCurve.png';
plot_Iterr = 'ItterationsCurve.png';
plot_Ploss = 'PowerLossCurve.png';
bar_Ploss = 'PowerLossChart.png';
bar_Fcost = 'FuelCostBar.png';
hvdc_Losses = 'HVDC_loses.png';
transmission_modes = ["HVAC","HVDC"];
source = ["6thermal","4thermal","2wind"];
% 分配输入与输出的各种参数
[power_loss,F_cost,iterrations,sw_loss,cond_loss,tl_loss,F_cost_inst] = deal(zeros);
demand = [120 150 180 210 240 270 300 330 360 390 420]; % 定义各个节点的负荷需求
load_demand_values = numel(demand); % 使用numel函数对矩阵的元素进行计数
print = fopen(doc_name,'w+');
% 定义全球变量,可用于所有函数
global fuel_coefficients B power_demand Pg_limits transmission_type ...
Cond_loss SW_loss TL_loss convergence_time start_timing DRi URi ...
n f_cost beta tao time instability inst_const
% 有5列燃料成本系数的燃料系数矩阵(发电机燃料消耗矩阵)
fuel_coefficients = [0.00375 2.00 240 0 0;
0.01750 1.75 200 0 0;
0.06250 1.00 220 40 0.008;
0.00834 3.25 200 30 0.009;
0.02500 3.00 220 0 0;
0.02500 3.00 190 0 0];
generator_limits = [50 200;20 80;15 50;10 35;10 30;12 40];% 定义发电机功率限制
% 发电机上下爬坡功率定义
DRi= [85 22 15 16 9 16];
URi= [65 12 12 8 6 8];
beta = 1.75;
tao = 2.85;
time = 10; % 发电机暂稳态时间定义
instability = false(); % 将第一次计算设定为没有不稳定因素
n = length(fuel_coefficients(:,1)); %返回fuel_coefficients变量的长度
%% 循坏开始
for type = 1:numel(transmission_modes)% 在每个模式中循环往复
transmission_type = transmission_modes(type);
fprintf(print,strcat('ECONOMIC DISPATCH FOR _', ...
' USING NOVEL BAT OPTIMIZATION ALGORITHM \n'));
%% Step 1:找到B矩阵
loss_coef = [0.000218 0.000103 0.000009 -0.000010 0.000002 0.000027
0.000103 0.000181 0.000004 -0.000015 0.000002 0.000030
0.000009 0.000004 0.000417 -0.000131 -0.000153 -0.000107
-0.000010 -0.000015 -0.000131 0.000221 0.000094 0.000050
0.000002 0.000002 -0.000153 0.000094 0.000243 -0.000000
0.000027 0.000030 -0.000107 0.000050 -0.000000 0.000358];