文章目录
- 局部搜索算法
- 内存限制
- 局部搜索算法
- 示例:n-皇后
- 爬山算法
- 随机重启爬山
- 模拟退火算法
- 局部剪枝搜索
- 遗传算法
- 小结
局部搜索算法
-
在某些规模太大的问题状态空间内,A*往往不够用

- 问题空间太大了
- 无法访问 f 小于最优的所有状态
- 通常,甚至无法储存整个边缘队列
-
解决方案
- 设计选择更好的启发式函数
- Greedy hill-climbing (fringe size = 1)
- Beam search (limited fringe size)
内存限制
- 瓶颈:内存不足,无法存储整个边缘队列
- 爬山搜索:
- 只有“最佳”节点保留在周围,没有边缘队列
- 通常按h优先选择继任者(贪婪的爬山)
- 与贪婪的回溯相比,它仍然有边缘队列
- 剪枝搜索(有限内存搜索)
- 介于两者之间:保持边缘中的K个节点
- 根据需要转储优先级最低的节点
- 可以单独按h(贪婪剪枝搜索)或h+g(有限内存A*)进行优先级排序
局部搜索算法
- 在许多优化问题中,通往目标的路径是不相关的;目标状态本身就是解决方案
- 状态空间=“完整”配置集(完全状态)
- 查找满足约束的配置,例如n皇后
- 在这种情况下,我们可以使用本地搜索算法
- 保持一个单一的“当前”状态,尝试改善它
- 直到你无法让它变得更好
- 恒定空间,适合在线和离线搜索
- 通常效率更高(但不完备)
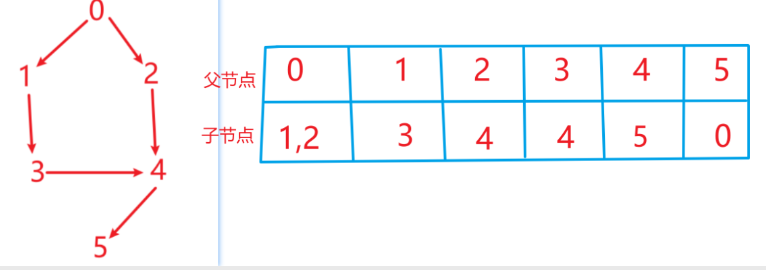
示例:n-皇后
- 将n个皇后区放在n×n板上,同一行、同一列或同一对角线上没有两个皇后区#

爬山算法
- 简单、概括的想法:
- 从任何地方开始
- 总是选择最好的邻居
- 如果没有邻居的分数比当前分数高,退出
- 这在理论上效果很糟糕,因为他不具有完备性(算法不会陷入死循环,即一定能结束)也不保证得到最优解
- 问题:根据初始状态,可能会陷入局部最大值

- 随机重新开始爬山算法一定程度克服了局部最大值
- 随机侧向移动逃离肩膀
- 但可能在最大值处循环
随机重启爬山
-
非常简单的修改:
- 当被卡住时,随机选择一个新的启动状态,然后从那里重新运行爬山
- 重复此操作k次
- 返回k个局部最优值中的最佳值
-
可以做到非常高效
-
每当使用爬山时都应该尝试
-
快速、易于实施;对于解决方案空间表面不太“颠簸”(即不太多局部最大值)的许多应用来说,效果很好
-
仍然以8皇后问题为例:

- h=直接或间接相互攻击的成对皇后数量
- 对于上述状态,h=17
- 一个局部最优解如下:h=1

模拟退火算法
-
思想: 通过允许一些“坏”动作,但逐渐降低其频率,来逃避局部最大值

-
可以证明:如果T下降得足够慢,那么模拟退火搜索将找到概率接近1的全局最优
-
广泛应用于超大规模集成电路布局、航空公司调度等
局部剪枝搜索
- 跟踪k个状态,而不仅仅是一个。
- 从k个随机生成的状态开始。
- 在每次迭代时,生成所有k个状态的所有后续状态。
- 如果任何一个是目标状态,则停止;否则,从完整列表中选择k个最佳继任者,然后重复。
- 像贪婪搜索一样,但始终保持K状态:

- 多种实用设置中的最佳选择
- 与并行运行的k个搜索不同!
- 找到好状态的搜索,会招募其他搜索加入他们
- 变量:分支大小,鼓励多样性?
- 问题:通常情况下,所有k个状态最终都在同一个局部山丘上
- 思想:随机选择k个继任者,偏向于优秀的继任者
遗传算法
- 遗传算法使用自然选择隐喻
- 通过组合两个父状态生成后续状态
- 从k个随机生成的状态开始(总体种群)
- 状态表示为有限字母表上的字符串(通常是0和1的字符串)
- 评价函数(适应度函数适应度函数). 值越高,状态越好。
- 通过选择、交叉和突变产生下一代状态(选择,杂交,变异)
- 示例:每个状态由8个数字表示,按照概率随机选择两对交叉,适应度就是互不攻击的皇后对数,概率就是适应度的占比


小结
- 局部搜索算法——通往目标的路径是不相关的;目标状态本身就是解决方案,保持单一的“当前”状态,并尝试改进它
- 登山搜索
- 根据初始状态,可能会陷入局部最大值
- 模拟退火搜索
- 通过允许一些“坏”的移动来逃避局部最大值,但逐渐降低其频率
- 局部剪枝搜索
- 跟踪k个状态,而不仅仅是一个
- 好的启发式搜索能大大提高搜索性能
- 但由于启发式搜索需要抽取与问题本身有关的特征信息,而这种特征信息的抽取有时会比较困难,因此盲目搜索仍不失为一种有用的搜索策略
- 好的搜索策略应该
- 引起运动—避免原地踏步
- 系统—避免兜圈
- 运用启发函数—缓解组合爆炸
- 搜索树 vs 搜索图
- 搜索树:结点有重复,但登记过程简单
- 搜索图:结点无重复,但登记过程复杂(每次都要查重)
- 省空间,费时间。