目录

1.算法流程简介

2.算法核心代码

3.算法效果展示

1.算法流程简介

#非线性规划模型求解:
#我们采用通用的minimize函数来求解
#minimize(f,x,method,bounds,contrains)
#f是待求函数
#x是代求的自变量
#method是求解方法
#bounds是取值范围边界
#contrains是约束条件
"""
#Question:
        min f=x1^2+x2^2+x3^2+8
        s.t.:
            x1^2-x2^2+x3^2>=0
            x1+x2^2+x3^2<=20
            -x1-x2^2+2=0
            x2+2x3^2=3
            x1,x2,x3>=0 
"""
#具体流程如下所示:
#1.设置待求函数和约束条件
#2.处理边界约束问题
#3.代入计算求解最优值

2.算法核心代码

#引用库和函数
import numpy as np
from scipy.optimize import minimize
from scipy import optimize as opt

#1.设置待求函数和约束条件
def cal_fun(x):
    return x[0]*x[0]+x[1]*x[1]+x[2]*x[2]+8
def cont1(x):
    return x[0] ** 2 - x[1] + x[2] ** 2#s.t.1
def cont2(x):
    return -(x[0] + x[1] ** 2 + x[2] ** 2 - 20)#s.t.2
def cont3(x):
	return -x[0] - x[1] ** 2 + 2#s.t.3
def cont4(x):
	return x[1] + 2 * x[2] ** 2 - 3#s.t.4

#2.处理边界约束问题
b=(0,None)
rbound=(b,b,b)

con1={'type':'ineq','fun':cont1}
con2={'type':'ineq','fun':cont2}
con3={'type':'eq','fun':cont3}
con4={'type':'eq','fun':cont4}
cons=([con1,con2,con3,con4])

#3.代入计算求解最优值
x=np.array([0,0,0])
ans=minimize(cal_fun,x,method='SLSQP',bounds=rbound,constraints=cons)
x_ans=ans.x
print("最优解:"+str(cal_fun(x_ans)))
print("最优解的方案是:x1="+str(x_ans[0]),"x2="+str(x_ans[1]))

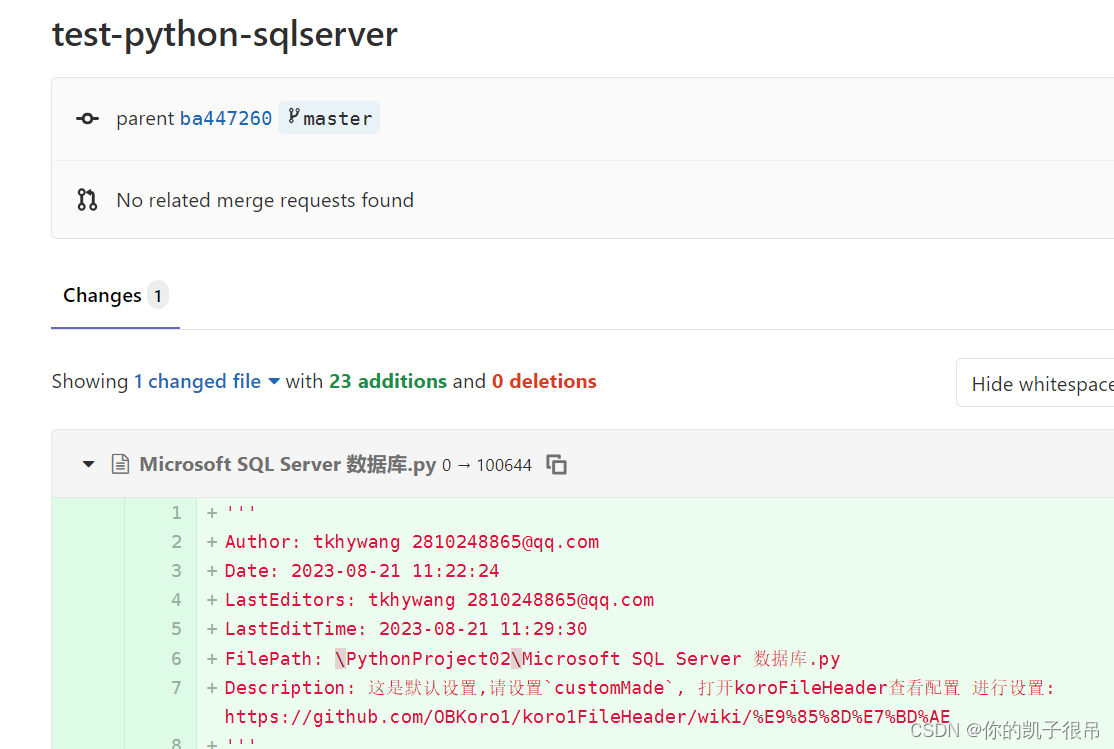
3.算法效果展示