本章gitee代码:计数排序
文章目录
- 🍇0. 前言
- 🍈1. 思路
- 🍉2. 代码实现
- 🍊3. 优势与缺陷
- 🍋4. 其他的非比较排序
- 🫴桶排序
- 🫴基数排序
🍇0. 前言
传统的排序方法通常需要逐个比较元素的大小,但非比较排序采用了一种不同的方法,即通过映射元素的值来统计相同元素的数量,然后将统计结果重新映射回原始序列,本章将介绍非比较排序中的计数排序。
如果对传统排序不熟悉的铁子可以查看此篇文章——数据结构——七大排序[源码+动图+性能测试]
🍈1. 思路
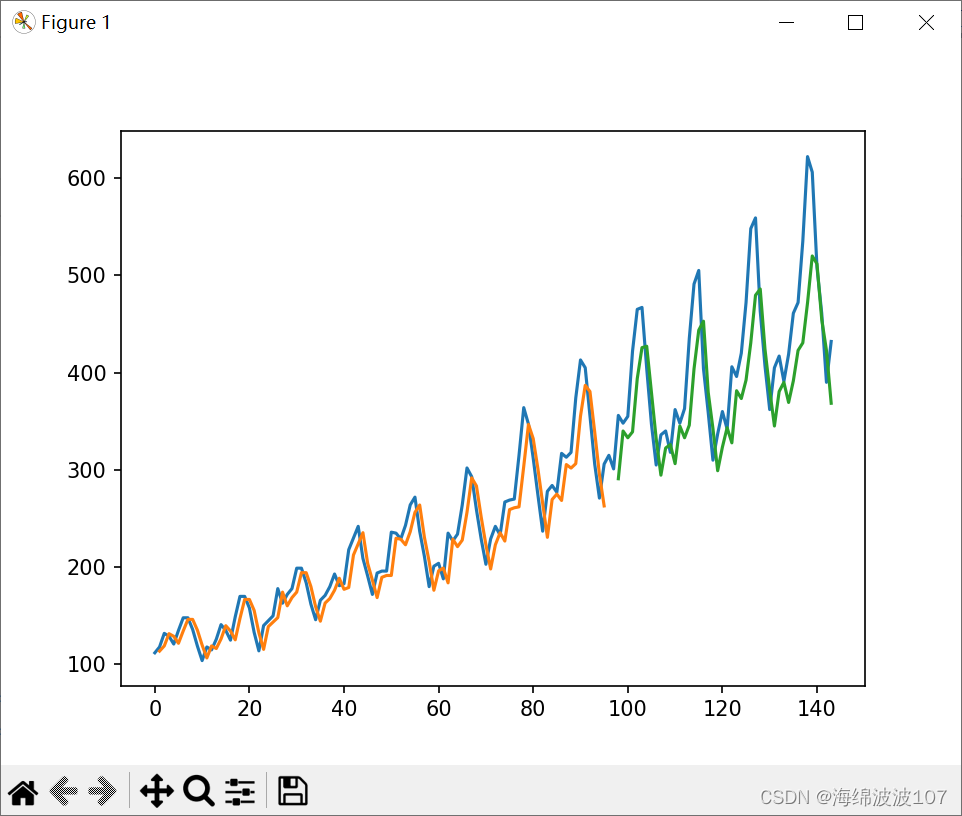
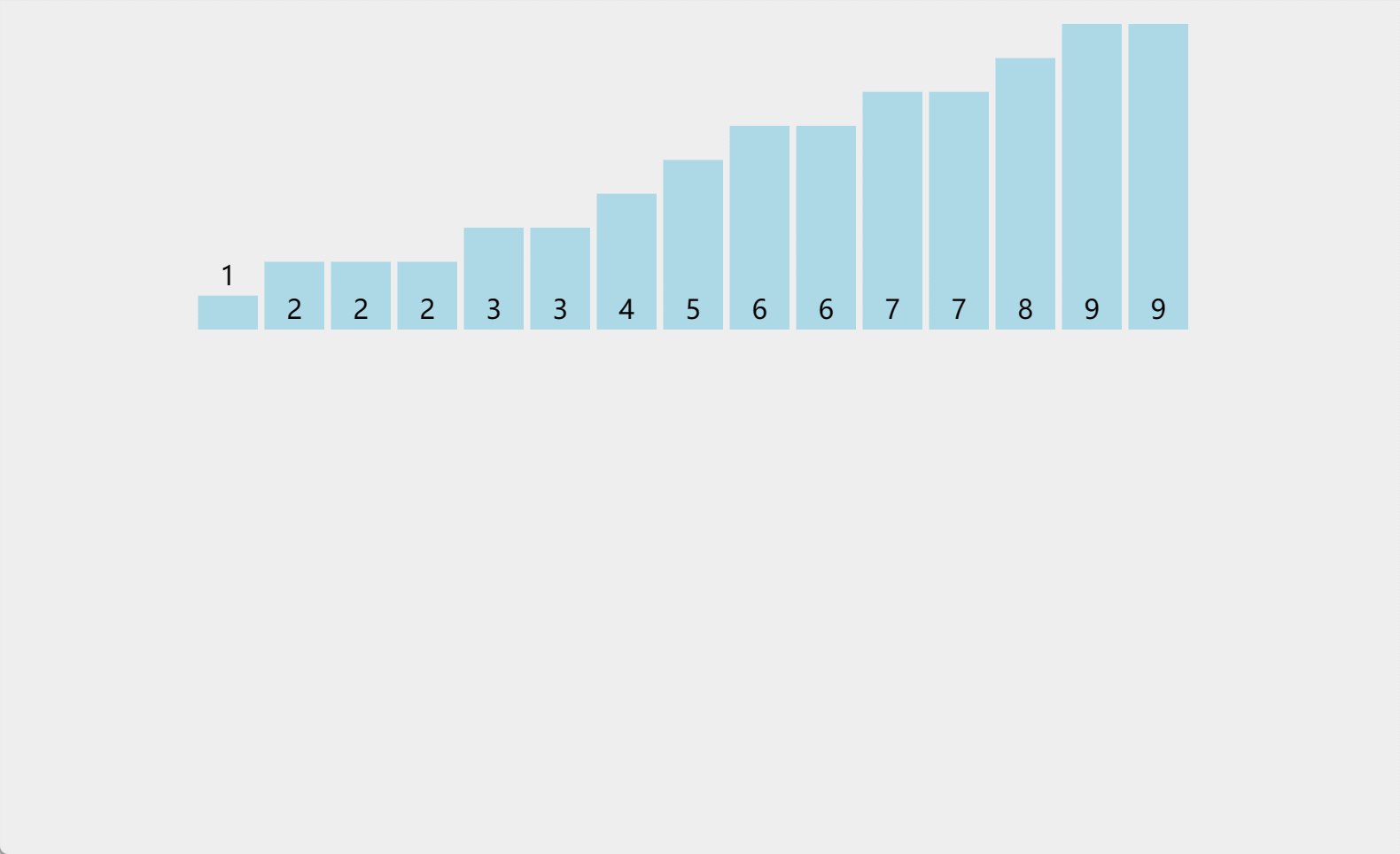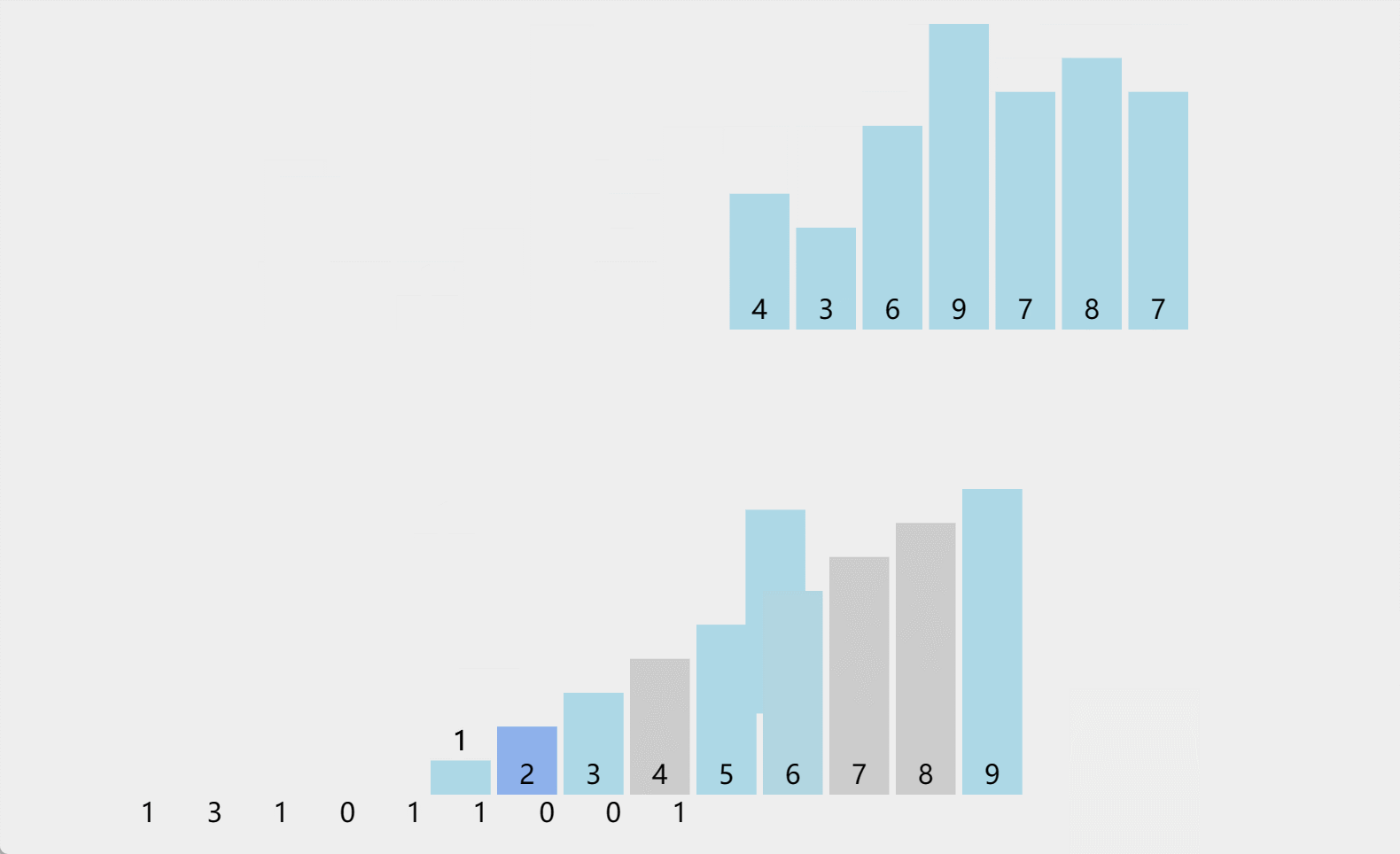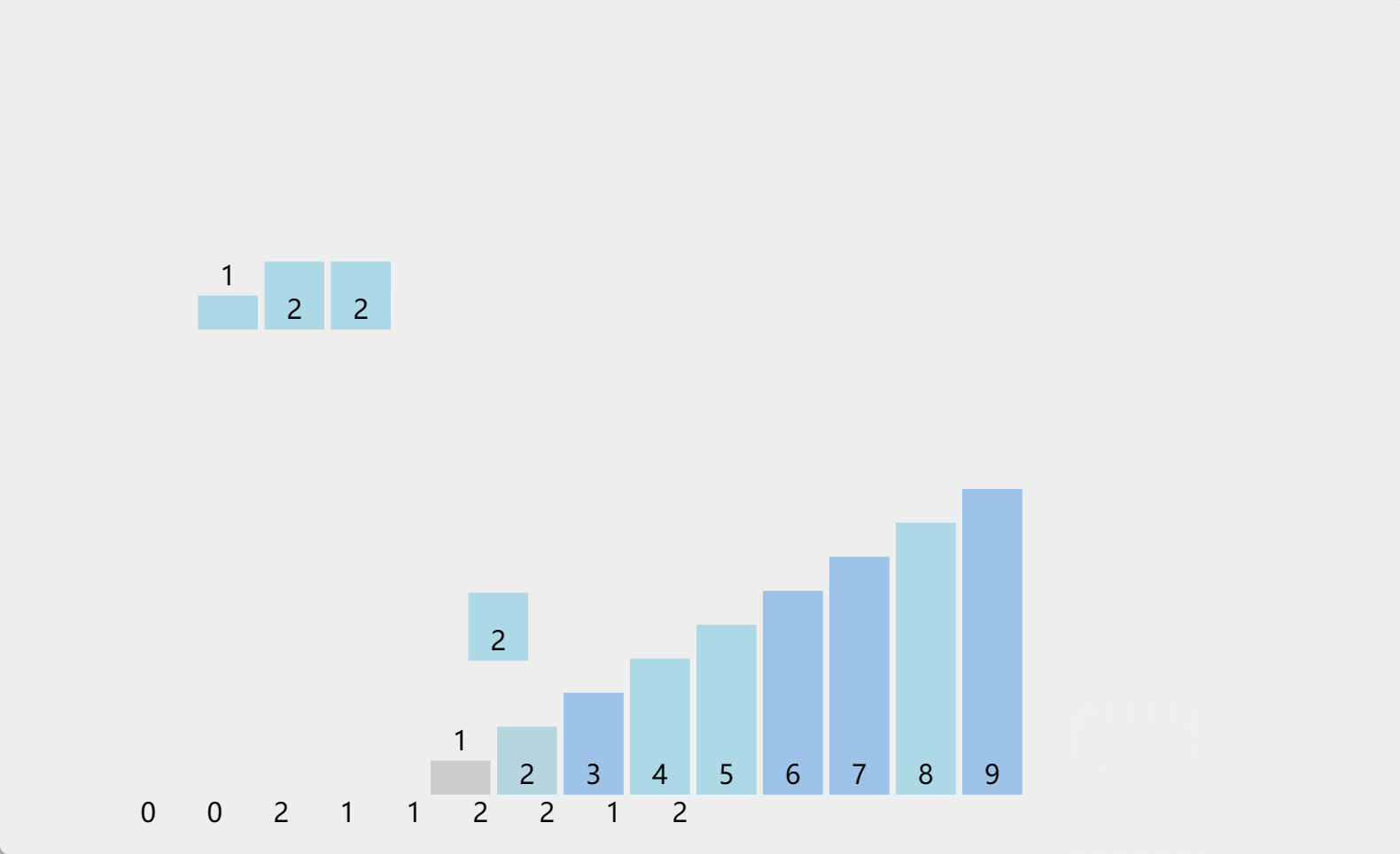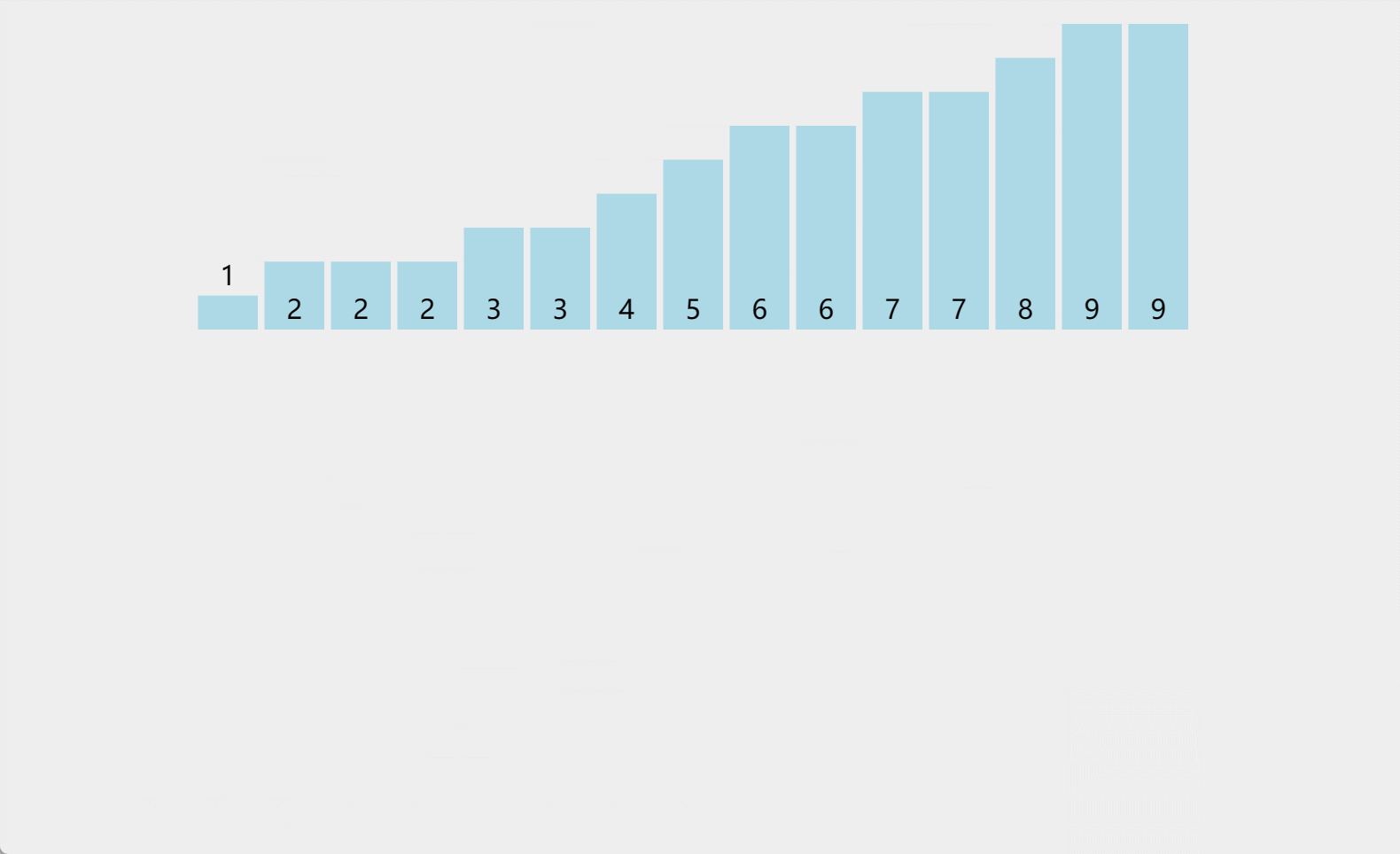
计数排序,开辟一个临时数组,初始值全部置0,然后遍历序列,将出现的元素对应下标进行统计,统计完毕之后,再出现归到原序列,形成有序序列。
然而,如果待排序序列中的值的范围较大,就会导致空间的浪费,例如,对于序列{100, 110, 120, 130…},我们需要为范围从0到99的元素都分配空间,这会造成大量的浪费。为了解决这个问题,我们可以采用相对映射的方式,先统计序列中的最大值和最小值,然后计算出值的范围。
🍉2. 代码实现
//小范围O(N+range)
void CountSort(int* a, int n)
{
int max = a[0];
int min = a[0];
//找最大最小值
for (int i = 0; i < n; i++)
{
if (a[i] > max)
max = a[i];
if (a[i] < min)
min = a[i];
}
int range = max - min + 1;
int* tmp = (int*)calloc(range, sizeof(int));
if (tmp == NULL)
{
perror("malloc fail\n");
}
//相对映射
for (int i = 0; i < n; i++)
{
int index = a[i] - min;
tmp[index]++;
}
int j = 0;
for (int i = 0; i < range; i++)
{
while (tmp[i]--)
a[j++] = i + min;
}
free(tmp);
}
🍊3. 优势与缺陷
- 优势: 计数排序在处理小范围数值的情况下性能强大,时间复杂度可达O(N),例如,对于考试成绩的统计范围在0~100之间的情况。
- 缺陷: 计数排序的缺陷也很明显。当数值范围较大时,会导致大量空间的浪费。此外,计数排序只适用于整数排序,无法很好地处理浮点数或字符的排序需求。
🍋4. 其他的非比较排序
🫴桶排序
桶排序是一种非比较排序算法,它将元素分散到多个桶中,然后分别对每个桶中的元素进行排序,最后合并所有桶的结果以得到有序序列。桶排序适用于元素均匀分布在一个范围内的情况,时间复杂度可以达到O(N)。它的思想类似于计数排序,但可以处理浮点数等不适用于计数排序的数据类型。
🫴基数排序
基数排序是一种多次应用桶排序的排序算法,它按照元素的每一位进行排序,从最低位到最高位,直到所有位都排完为止。基数排序适用于对整数或字符串等有固定位数表示的数据进行排序,时间复杂度为O(kN),其中k为元素的最大位数。
Tips:
这两种排序在日常中并不常用,可以只做了解
主要还是得掌握传统的排序思想,非比较排序应用场景较少,具体还得看使用场景。
那么本次的分享就到这里咯,我们下期再见,如果还有下期的话。