一、一些概念
训练误差(training error) 是指,模型在训练数据集上计算得到的误差。
泛化误差(generalization error) 是指,模型应⽤在同样从原始样本的分布中抽取的⽆限多数据样本时,模型误差的期望。
我们永远不能准确地计算出泛化误差。在实际中,我们只能通过将模型应⽤于⼀个独⽴的测试集来估计泛化误差,该测试集由随机选取的、未曾在训练集中出现的数据样本构成。
模型复杂性:通常对于神经⽹络,我们认为需要更多训练迭代的模型⽐较复杂,⽽需要“早停”(earlystopping)的模型(即较少训练迭代周期)就不那么复杂。
验证集:
我们决不能依靠测试数据进⾏模型选择。然⽽,我们也不能仅仅依靠训练数据来选择模型,因为我们⽆法估计训练数据的泛化误差。解决此问题的常⻅做法是将我们的数据分成三份,除了训练和测试数据集之外,还增加⼀个验证数据集(validation dataset),也叫验证集(validation set)。
但现实是验证数据和测试数据之间的边界十分模糊,因此我们实际上是在使⽤应该被正确地称为训练数据和验证数据的数据集,并没有真正的测试数据集。
K折交叉验证:
当训练数据稀缺时,我们甚⾄可能⽆法提供⾜够的数据来构成⼀个合适的验证集。这个问题的⼀个流⾏的解决⽅案是采⽤K折交叉验证。
这⾥,原始训练数据被分成K个不重叠的⼦集。然后执⾏K次模型训练和验证,每次在K − 1个⼦集上进⾏训练,并在剩余的⼀个⼦集(在该轮中没有⽤于训练的⼦集)上进⾏验证。
最后,通过对K次实验的结果取平均来估计训练和验证误差。
⽋拟合(underfitting): 训练误差和验证误差都很严重,但它们之间仅有⼀点差距。
过拟合(overfitting): 当我们的训练误差明显低于验证误差时要⼩⼼,这表明严重的过拟合.
注意,过拟合并不总是⼀件坏事。特别是在深度学习领域,众所周知,最好的预测模型在训练数据上的表现往往⽐在保留(验证)数据上好得多。
是否过拟合或⽋拟合可能取决于模型复杂性和可⽤训练数据集的⼤⼩。
(1)模型复杂性
⾼阶多项式函数⽐低阶多项式函数复杂得多。⾼阶多项式的参数较多,模型函数的选择范围较⼴。
因此在固定训练数据集的情况下,⾼阶多项式函数相对于低阶多项式的训练误差应该始终更低(最坏也是相等)
(2)数据集的⼤⼩
训练数据集中的样本越少,我们就越有可能(且更严重地)过拟合。
随着训练数据量的增加,泛化误差通常会减⼩。此外,⼀般来说,更多的数据不会有什么坏处。
二、过拟合和欠拟合案例
%matplotlib inline
import os
os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE"
import math
import numpy as np
import torch
from torch import nn
'''
二、过拟合和欠拟合
给定x,我们将使⽤以下三阶多项式来⽣成训练和测试数据的标签:
y = 5 + 1.2x − 3.4 * x^2/2! + 5.6 * x^3 / 3! + ϵ
噪声项ϵ服从均值为0且标准差为0.1的正态分布。
'''
# 1、为训练集和测试集各⽣成100个样本。
n_train = 100
n_test = 100
# 多项式的最大阶数
max_degree = 20
true_w = np.zeros(max_degree)
true_w[0:4] = np.array([5, 1.2, -3.4, 5.6])
features = np.random.normal(size=(n_train + n_test, 1))
np.random.shuffle(features)
poly_features = np.power(features, np.arange(max_degree).reshape(1, -1))
for i in range(max_degree):
poly_features[:, i] /= math.gamma(i + 1) # gamma(n)=(n-1)!
# labels的维度:(n_train+n_test,)
labels = np.dot(poly_features, true_w)
labels += np.random.normal(scale=0.1, size=labels.shape)
# NumPy ndarray转换为tensor
true_w, features, poly_features, labels = \
[torch.tensor(x, dtype=torch.float32) for x in [true_w, features, poly_features, labels]
]
true_w,features[:2], poly_features[:2, :], labels[:2]

# 2、评估给定数据集上的损失
from AccumulatorClass import Accumulator
from torch.utils import data
def evaluate_loss(net, data_iter, loss):
metric = Accumulator(2)
for X,y in data_iter:
out = net(X)
y = y.reshape(out.shape)
l = loss(out, y)
metric.add(l.sum(), l.numel())
return metric[0] / metric[1]
# 3、定义训练函数
def load_array(data_arrays, batch_size, is_train=True):
"""构造⼀个PyTorch数据迭代器"""
dataset = data.TensorDataset(*data_arrays)
return data.DataLoader(dataset, batch_size, shuffle=is_train)
from EpochTrainClass import epoch_train
from matplotlib import pyplot as plt
from IPython import display
def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):
"""设置matplotlib的轴"""
axes.set_xlabel(xlabel)
axes.set_ylabel(ylabel)
axes.set_xscale(xscale)
axes.set_yscale(yscale)
axes.set_xlim(xlim)
axes.set_ylim(ylim)
if legend:
axes.legend(legend)
axes.grid()
class Animator:
"""在动画中绘制数据"""
def __init__(self, xlabel=None, ylabel=None, legend=None, xlim=None,
ylim=None, xscale='linear', yscale='linear',
fmts=('-', 'm--', 'g-.', 'r:'), nrows=1, ncols=1,
figsize=(3.5, 2.5)):
# 增量地绘制多条线
if legend is None:
legend = []
self.fig, self.axes = plt.subplots(nrows, ncols, figsize=figsize)
if nrows * ncols == 1:
self.axes = [self.axes, ]
# 使用lambda函数捕获参数
self.config_axes = lambda: set_axes(
self.axes[0], xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
self.X, self.Y, self.fmts = None, None, fmts
def add(self, x, y):
# 向图表中添加多个数据点
if not hasattr(y, "__len__"):
y = [y]
n = len(y)
if not hasattr(x, "__len__"):
x = [x] * n
if not self.X:
self.X = [[] for _ in range(n)]
if not self.Y:
self.Y = [[] for _ in range(n)]
for i, (a, b) in enumerate(zip(x, y)):
if a is not None and b is not None:
self.X[i].append(a)
self.Y[i].append(b)
self.axes[0].cla()
for x, y, fmt in zip(self.X, self.Y, self.fmts):
self.axes[0].plot(x, y, fmt)
self.config_axes()
display.display(self.fig)
display.clear_output(wait=True)
def train(train_features,test_features,train_labels,test_labels,num_epochs=400):
# 均方差损失
loss = nn.MSELoss(reduction='none')
input_shape = train_features.shape[-1]
net = nn.Sequential(
nn.Linear(input_shape, 1, bias=False) # 不设置偏置,因为我们已经在多项式中实现了它
)
batch_size = min(10, train_labels.shape[0])
train_iter = load_array(
(train_features, train_labels.reshape(-1,1)),
batch_size
)
test_iter = load_array(
(test_features, test_labels.reshape(-1,1)),
batch_size,
is_train=False
)
trainer = torch.optim.SGD(net.parameters(), lr=0.01)
animator = Animator(xlabel='epoch', ylabel='loss', yscale='log',
xlim=[1, num_epochs], ylim=[1e-3, 1e2],
legend=['train', 'test'])
for epoch in range(num_epochs):
epoch_train(net, train_iter, loss, trainer)
if epoch == 0 or (epoch + 1) % 20 == 0:
animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss),
evaluate_loss(net, test_iter, loss)))
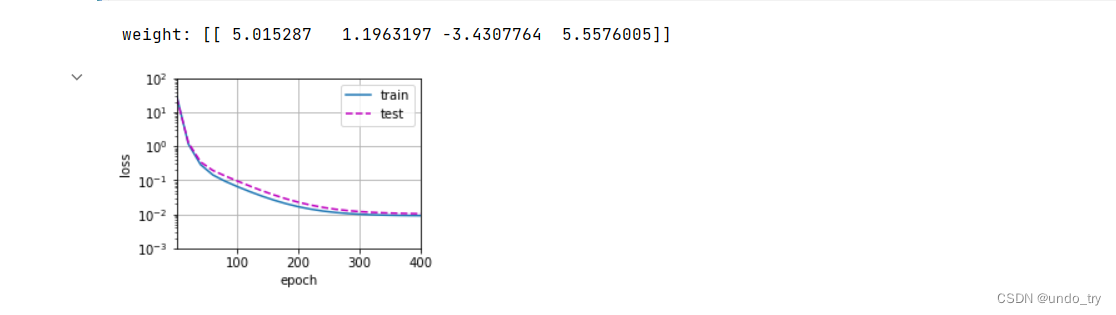
print('weight:', net[0].weight.data.numpy())
(1)正常情况
'''
(1) 正常情况
我们将⾸先使⽤三阶多项式函数,它与数据⽣成函数的阶数相同。
结果表明,该模型能有效降低训练损失和测试损失。学习到的模型参数也接近真实值w = [5, 1.2, −3.4, 5.6]。
'''
# 使用3阶多项式进行拟合
# 从多项式特征中选择前4个维度,即1,x,x^2/2!,x^3/3!
train(
poly_features[:n_train, :4],
poly_features[n_train:, :4],
labels[:n_train],
labels[n_train:]
)
(2)线性函数拟合(⽋拟合)
'''
(2)线性函数拟合(⽋拟合)
在最后⼀个迭代周期完成后,训练损失仍然很⾼。
'''
# 从多项式特征中选择前2个维度,即1和x
train(
poly_features[:n_train, :2],
poly_features[n_train:, :2],
labels[:n_train],
labels[n_train:]
)

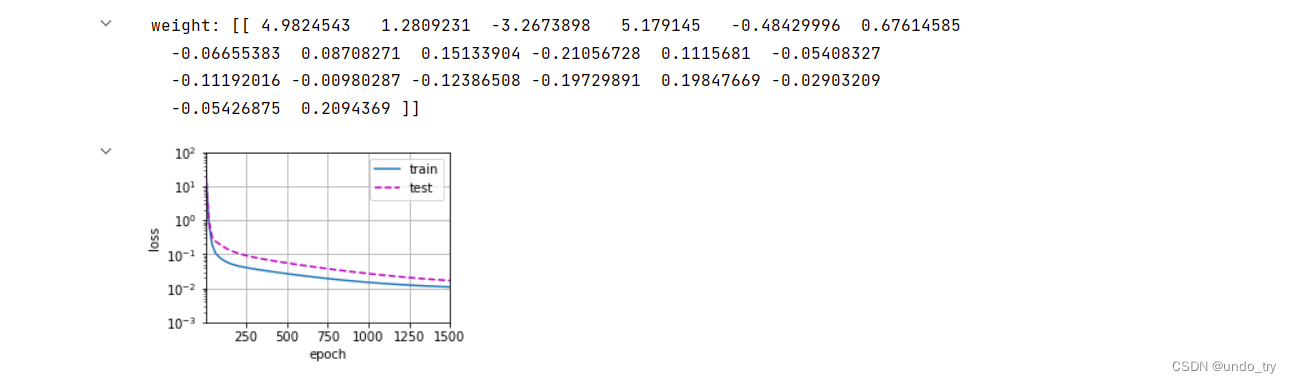
(3)⾼阶多项式函数拟合(过拟合)
'''
(3)、⾼阶多项式函数拟合(过拟合)
虽然训练损失可以有效地降低,但测试损失仍然很⾼。
'''
# 从多项式特征中选取所有维度
train(
poly_features[:n_train, :],
poly_features[n_train:, :],
labels[:n_train],
labels[n_train:],
num_epochs=1500
)
三、利用权重衰减解决过拟合
最常⽤⽅法是将其范数作为惩罚项加到最⼩化损失的问题中。将原来的训练⽬标最⼩化训练标签上的预测损失,调整为最⼩化预测损失和惩罚项之和。
在训练参数化机器学习模型时,权重衰减(weight decay)是最⼴泛使⽤的正则化的技术之⼀,它通常也被称为L2正则化(是更为⼀般的Lp范数的特殊情况)。
L2正则化线性模型构成经典的岭回归(ridge regression)算法,L1正则化线性回归是统计学中类似的基本模型,通常被称为套索回归(lasso regression)。
使⽤L2范数的⼀个原因是它对权重向量的⼤分量施加了巨⼤的惩罚。这使得我们的学习算法偏向于在⼤量特征上均匀分布权重的模型。在实践中,这可能使它们对单个变量中的观测误差更为稳定。
相⽐之下,L1惩罚会导致模型将权重集中在⼀⼩部分特征上,⽽将其他权重清除为零。这称为特征选择(feature selection),这可能是其他场景下需要的。
(1) 权重衰减在高维线性回归的应用-手动实现
'''
d
y = 0.05 + ∑ 0.01 * xi + ϵ
i=1
'''
'1、模型生成数据'
# 设置d为200,训练集数据为20,测试集数据100,5为批量大小
n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05
def get_data(w, b, num_samples=1000):
"""⽣成y=Xw+b+噪声"""
X = torch.normal(0, 1, (num_samples, len(w)))
y = torch.matmul(X, w) + b
y += torch.normal(0, 0.01, y.shape)
return X,y.reshape((-1, 1))
features,labels = get_data(true_w,true_b)
# 生成训练集和测试集
train_data = get_data(true_w, true_b, n_train)
test_data = get_data(true_w, true_b, n_test)
# 构造PyTorch数据迭代器
train_iter = load_array(train_data, batch_size)
test_iter = load_array(test_data, batch_size)
'2、初始化模型参数'
def init_params():
w = torch.normal(
0,1,size=(num_inputs, 1),requires_grad=True
)
b = torch.zeros(
1,requires_grad=True
)
return [w,b]
w,b = init_params()
'3、定义L2范数惩罚'
# 实现这⼀惩罚最⽅便的⽅法是对所有项求平⽅后并将它们求和。
def l2_penalty(w):
return torch.sum(w.pow(2)) / 2
l2_penalty(w)
'4、训练'
# 计算线性模型的输出, 我们只需计算输入特征(f{X})和模型权重(w)的矩阵-向量乘法后加上偏置(b)
def line_alg(X, w, b):
return torch.matmul(X, w) + b
# 需要计算损失函数的梯度,所以我们应该先定义损失函数。
def square_loss(y_hat,y):
return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
# 小批量随机梯度下降
def mini_batch_sgd(params, lr, batch_size):
# torch.no_grad是一个类一个上下文管理器,disable梯度计算。
# disable梯度计算对于推理是有用的,当你确认不会调用Tensor.backward()的时候。这可以减少计算所用内存消耗。
# 这个模式下,每个计算结果的requires_grad=False,尽管输入的requires_grad=True。
with torch.no_grad():
for param in params:
param -= lr * param.grad / batch_size
param.grad.zero_()
def train_process(lambd):
# 初始化权重和偏置
w, b = init_params()
net = lambda X: line_alg(X, w, b)
loss = square_loss
num_epochs = 100
lr = 0.003
animator = Animator(
xlabel='epochs', ylabel='loss', yscale='log',
xlim=[5, num_epochs], legend=['train', 'test']
)
for epoch in range(num_epochs):
for X,y in train_iter:
# 增加l2范数
l = loss(net(X), y) + lambd * l2_penalty(w)
l.sum().backward()
mini_batch_sgd([w, b], lr, batch_size)
if (epoch + 1) % 5 == 0:
animator.add(epoch + 1,
(evaluate_loss(net, train_iter, loss),evaluate_loss(net, test_iter, loss))
)
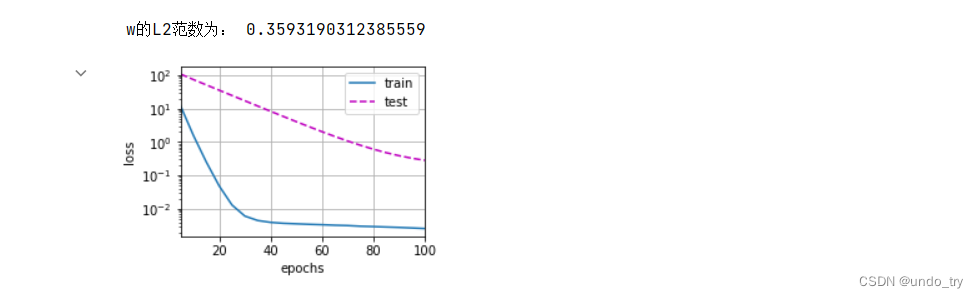
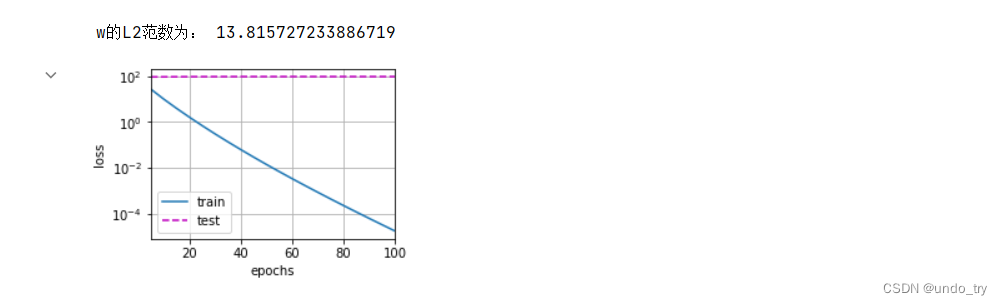
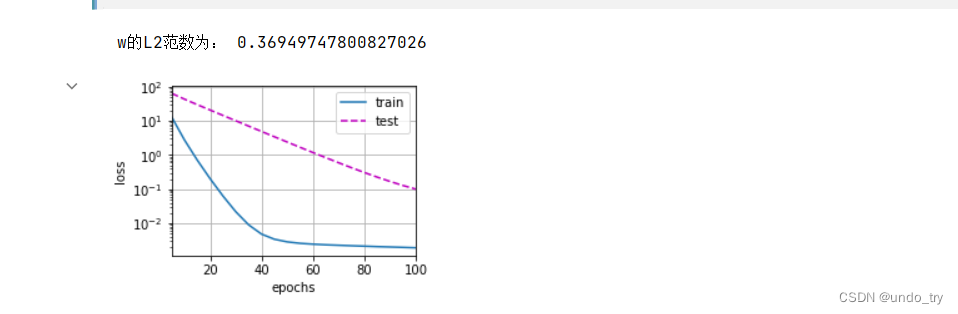
print('w的L2范数为:', torch.norm(w).item())
# 忽略正则化项进行训练
train_process(lambd=0)
# 这⾥训练误差有了减少,但测试误差没有减少,这意味着出现了严重的过拟合。
# 使用权重衰减进行训练
train_process(lambd=3)
# 注意,在这⾥训练误差增⼤,但测试误差减⼩。这正是我们期望从正则化中得到的效果。
(2) 权重衰减在高维线性回归的应用-高级api
'''
d
y = 0.05 + ∑ 0.01 * xi + ϵ
i=1
由于权重衰减在神经⽹络优化中很常⽤,深度学习框架为了便于我们使⽤权重衰减,将权重衰减集成到优化算法中,以便与任何损失函数结合使⽤。
'''
def train_high_api(wd):
net = nn.Sequential(
nn.Linear(num_inputs,1)
)
for param in net.parameters():
param.data.normal_()
loss = nn.MSELoss(reduction='none')
num_epochs = 100
lr = 0.003
# 偏置参数没有衰减
trainer = torch.optim.SGD(
[{"params":net[0].weight,'weight_decay': wd},
{"params":net[0].bias}],
lr=lr
)
animator = Animator(
xlabel='epochs', ylabel='loss', yscale='log',
xlim=[5, num_epochs], legend=['train', 'test']
)
for epoch in range(num_epochs):
for X,y in train_iter:
trainer.zero_grad()
l = loss(net(X), y)
l.mean().backward()
trainer.step()
if (epoch + 1) % 5 == 0:
animator.add(epoch + 1,
(evaluate_loss(net, train_iter, loss),evaluate_loss(net, test_iter, loss))
)
print('w的L2范数为:', net[0].weight.norm().item())
# 这些图看起来和我们从零开始实现权重衰减时的图相同。然⽽,它们运⾏得更快,更容易实现。
# 正则化是处理过拟合的常⽤⽅法:在训练集的损失函数中加⼊惩罚项,以降低学习到的模型的复杂度
train_high_api(0)
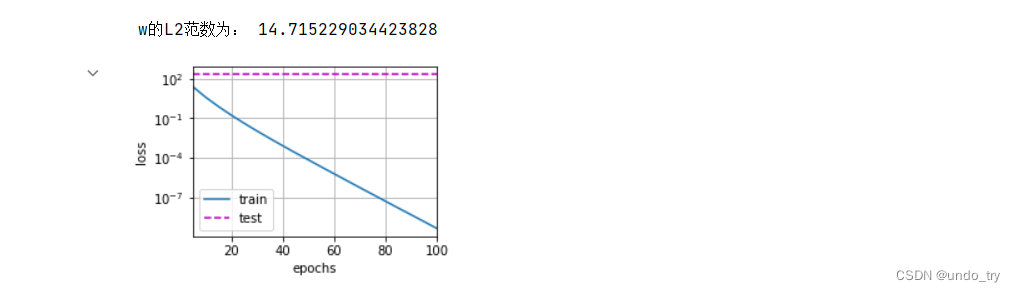
train_high_api(3)