题目描述

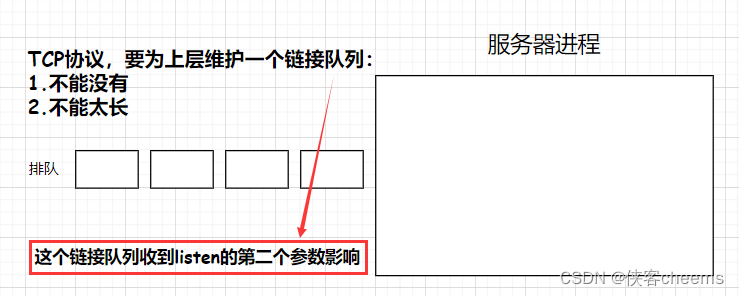
机器人走一个迷宫,给出迷宫的x和y(x*y的迷宫)并且迷宫中有障碍物,输入k表示障碍物有k个,并且会将障碍物的坐标挨个输入.
机器人从0,0的位置走到x,y的位置并且只能向x,y增加的方向走,不能回退.
如代码类注释展示的样子,#表示可以走的方格,0代表障碍,机器人从0,0的位置只能向下或者向前走到出口.
其中会有不可达方格和陷阱方格.不可达方格为第四行前三个,该机器人在行走路径上不可能走到的方格,陷阱方格如第一行最后两个,走进之后则不能抵达终点.
要求: 输出陷阱和不可达方格方格数量

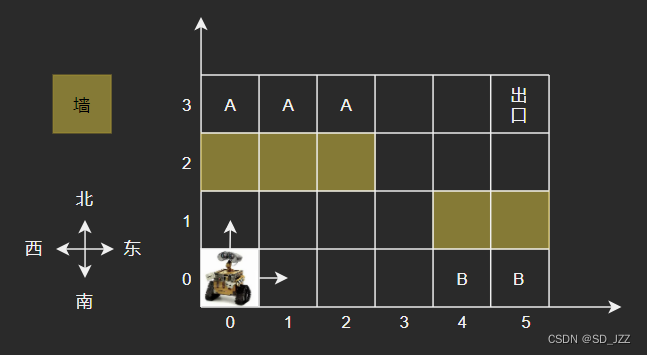
1.房间有 X*Y 的方格组成，例如下图为 6*4 的大小。每一个放个以坐标 (x,y) 描述
2.机器人固定从方格(,) 出发，只能向东或者向北前进出口固定为房间的最东北角，如下图的方格(5,3)。用例保证机器人可以从入口走到出口。
3.房间有些方格是墙壁，如 (4,1)机器人不能经过那儿。
4.有些地方是一旦到达就无法走到出口的，如标记为 B 的方格，称之为陷阱方格
5.有些地方是机器人无法达到的，如标记为 A 的方格，称之为不可达方格，不可达方格不包括墙壁所在的位置6.如下实例图中，陷阱方格有 2 个，不可达方格有 3 个。
7.请为该机器人实现 路径规划Q功能: 给定房间大小，墙壁位置，请计算出陷阱方格与不可达方格分别有多少个

代码实现

# coding:utf-8
"""
@Date   :2023/7/22
@Title  ：机器人走迷宫
@discript：https://dream.blog.csdn.net/article/details/128986089
"""


def robotWalkMaze(x, y, obs):
    dp = [['#'] * y for _ in range(x)]

    # 把墙壁坐标对应的结果标记为0
    for ob in obs:
        i, j = ob
        dp[i][j] = 0

    def dfs(x_, y_):
        if x_ == x - 1 and y_ == y - 1:  # 如果坐标等于出口位置，返回路线可用，标记1
            dp[x_][y_] = 1
            return 1
        elif x_ >= x or y_ >= y or dp[x_][y_] == 0:  # 如果坐标大于等于边界，或者dp中标记为0，即墙壁，这路线标记为-1，不可用
            return -1
        elif dp[x_][y_] != '#':  # 如果当前位置不等于#，即已经被标记过，返回该标记即可
            return dp[x_][y_]
        else:  # 按照深度优先算法先向下走，再向右走
            down = dfs(x_ + 1, y_)
            right = dfs(x_, y_ + 1)
            if down == -1 and right == -1:  # 如果当前位置标记为向下和向右都标记为-1，即说明该位置是陷阱方块
                dp[x_][y_] = -1
            else:
                dp[x_][y_] = max(down, right)  # 位置信息取向下或者向右最大值，其实就是只要有1就ok
            return dp[x_][y_]

    dfs(0, 0)
    r1 = sum(line.count(-1) for line in dp)
    r2 = sum(line.count('#') for line in dp)  # 位置标记没被更新，说明是不可达的方块
    return r1, r2


x, y = map(int, input('X,Y:').split())
obss = []

for _ in range(int(input('N:'))):
    obj = tuple(map(int, input('location:').split(' ')))
    obss.append(obj)

c1, c2 = robotWalkMaze(x, y, obss)
print(c1, c2)