AtCoder Beginner Contest 315 Ex. Typical Convolution Problem(分治NTT/全在线卷积)

题目

给定长为n(n<=2e5)的序列a，第i个数ai(0<=ai<998244353)

求序列f，满足式子如下：

$eq?f_%7Bk%7D%20%3D%20%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%201%2C%20k%3D0%20%5C%5C%20a_%7Bk%7D*%5Csum_%7Bi+j%3Cn%7Df_%7Bi%7D*f_%7Bj%7D%281%5Cleq%20k%20%5Cleq%20n%29%20%5Cend%7Bmatrix%7D%5Cright.$

思路来源

jiangly代码/力扣群友tdzl2003/propane/自己的乱搞

题解

分治NTT，考虑[l,mid]对[mid+1,r]的贡献，

但是，手玩一下就会发现有个问题

举个例子，

1. [l,mid]=[0,1]，[mid+1,r]=[2,3]，那么右半边f2会加上f0*(f0+f1)+f1*f0，贡献完整

2. [l,mid]=[5,6]，[mid+1,r]=[7,8]，那么右半边f7会加上f5*(f0+f1)+f6*f0

相当于只有一半贡献，比如有f5*f0，没有f0*f5，

因为考虑f0所在区间对右的贡献时，f5还没算出来

对于第二种情况，贡献就需要乘以2

这两种情况会混在一起导致很难算么，答案是不会的

考虑第一次出现贡献完整，不需要*2的项时，

左边两个下标最小，右边下标最大，也就是l+l=r-1，满足2*l<r

由于分治NTT是分治的完整的2的幂次的区间，左右半段等长，

观察不难发现~~（jiangly代码告诉我们）~~只有l=0时，才会出现2*l<r

所以，分类讨论两种情况即可

Bonus

官方题解/群友给出了全在线卷积/半在线卷积的解法，更好理解，

一边卷积求第i项，一边维护卷积的前缀和

大概看了看是构造出了一个矩阵，

数字表示该数加入的时候算哪些矩阵，

每个矩阵对应一个边长规模的卷积

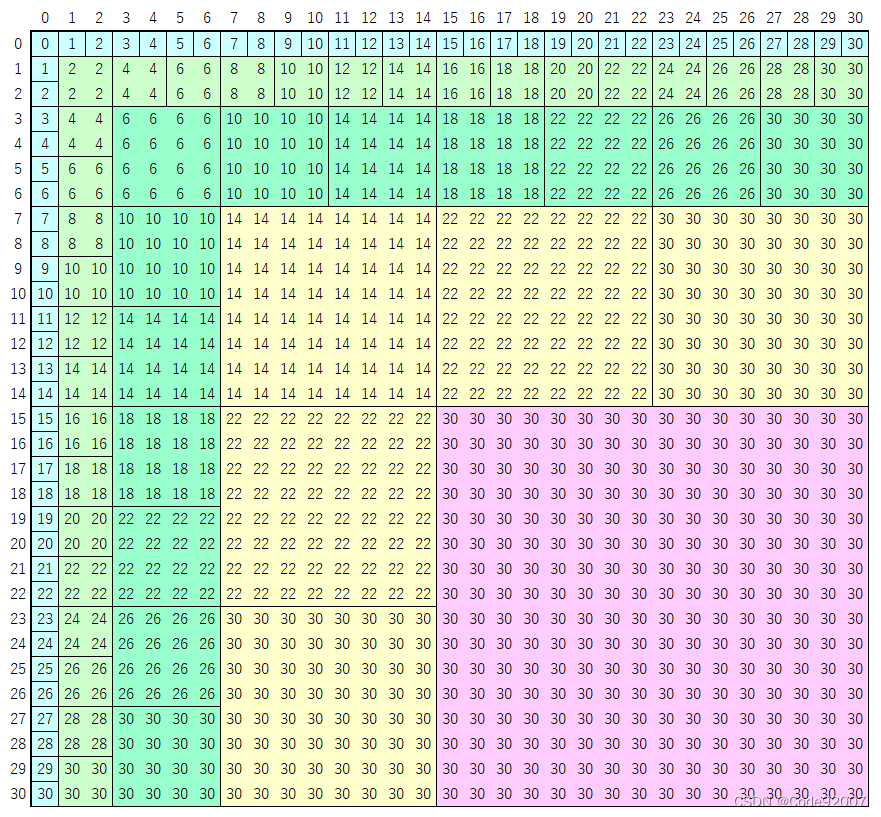
从而保证任何时刻均摊都是n(logn)^2，可以考虑以后整理个板子（咕）……

代码1（参考）

时间大概是代码2的一半

l=r处求f[l]的值，卷积的前缀和也是在此处算的

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<cmath>
#include<vector>
using namespace std;
#define ll long long
#define ull unsigned ll
const int N = 1<<20, P = 998244353;
const int Primitive_root = 3;
struct Z{
    int x;
    Z(const int _x=0):x(_x){}
    Z operator +(const Z &r)const{ return x+r.x<P?x+r.x:x+r.x-P;}
    Z operator -(const Z &r)const{ return x<r.x?x-r.x+P:x-r.x;}
    Z operator -()const{ return x?P-x:0;}
    Z operator *(const Z &r)const{ return static_cast<ull>(x)*r.x%P;}
    Z operator +=(const Z &r){ return x=x+r.x<P?x+r.x:x+r.x-P, *this;}
    Z operator -=(const Z &r){ return x=x<r.x?x-r.x+P:x-r.x, *this;}
    Z operator *=(const Z &r){ return x=static_cast<ull>(x)*r.x%P, *this;}
    friend Z Pow(Z, int);
    pair<Z,Z> Mul(pair<Z,Z> x, pair<Z,Z> y, Z f)const{
        return make_pair(
            x.first*y.first+x.second*y.second*f,
            x.second*y.first+x.first*y.second
        );
    }
};
Z Pow(Z x, int y=P-2){
    Z ans=1;
    for(; y; y>>=1, x=x*x) if(y&1) ans=ans*x;
    return ans;
}
namespace Poly{
    Z w[N];
    Z Inv[N];
    vector<Z> ans;
    vector<vector<Z> > p;
    ull F[N];
    int Get_root(){
		static int pr[N],cnt;
		int n=P-1,sz=(int)(sqrt(n)),root=-1;
		for(int i=2;i<=sz;++i){if(n%i==0)pr[cnt++]=i;while(n%i==0)n/=i;}
		if(n>1)pr[cnt++]=n;
		for(int i=1;i<P;++i){
			if(Pow((Z)i,P-1).x==1){
				bool fl=true;
				for(int j=0;j<cnt;++j){
					if(Pow(i,(P-1)/pr[j]).x==1){
						fl=false;break;
					}
				}
				if(fl){root=i;break;}
			}
		}
		return root;
	}
    void Init(){
    	//printf("root:%d\n",Primitive_root=Get_root()); 先求出来原根然后当const用 
        for(int i=1; i<N; i<<=1){
            w[i]=1;
            Z t=Pow((Z)Primitive_root, (P-1)/i/2);
            for(int j=1; j<i; ++j) w[i+j]=w[i+j-1]*t;
        }
        Inv[1]=1;
        for(int i=2; i<N; ++i) Inv[i]=Inv[P%i]*(P-P/i);
    }
    int Get(int x){ int n=1; while(n<=x) n<<=1; return n;}
    int Mod(int x){ return x<P?x:x-P;}
    void DFT(vector<Z> &f, int n){
        if((int)f.size()!=n) f.resize(n);
        for(int i=0, j=0; i<n; ++i){
            F[i]=f[j].x;
            for(int k=n>>1; (j^=k)<k; k>>=1);
        }
        if(n<=4){
            for(int i=1; i<n; i<<=1) for(int j=0; j<n; j+=i<<1){
                Z *W=w+i;
                ull *F0=F+j, *F1=F+j+i;
                for(int k=j; k<j+i; ++k, ++W, ++F0, ++F1){
                    ull t=(*F1)*(W->x)%P;
                    (*F1)=*F0+P-t, (*F0)+=t;
                }
            }
        }
        else{
            for(int j=0; j<n; j+=2){
                int t=F[j+1];
                F[j+1]=Mod(F[j]+P-t), F[j]=Mod(F[j]+t);
            }
            for(int j=0; j<n; j+=4){
                int t0=F[j+2], t1=F[j+3]*w[3].x%P;
                F[j+2]=F[j]+P-t0, F[j]+=t0;
                F[j+3]=F[j+1]+P-t1, F[j+1]+=t1;
            }
            for(int i=4; i<n; i<<=1) for(int j=0; j<n; j+=i<<1){
                Z *W=w+i;
                ull *F0=F+j, *F1=F+j+i;
                for(int k=j; k<j+i; k+=4, W+=4, F0+=4, F1+=4){
                    int t0=(W->x)**F1%P;
                    int t1=(W+1)->x**(F1+1)%P;
                    int t2=(W+2)->x**(F1+2)%P;
                    int t3=(W+3)->x**(F1+3)%P;
                    *F1=*F0+P-t0, *F0+=t0;
                    *(F1+1)=*(F0+1)+P-t1, *(F0+1)+=t1;
                    *(F1+2)=*(F0+2)+P-t2, *(F0+2)+=t2;
                    *(F1+3)=*(F0+3)+P-t3, *(F0+3)+=t3;
                }
            }
        }
        for(int i=0; i<n; ++i) f[i]=F[i]%P;
    }
    void IDFT(vector<Z> &f, int n){
        f.resize(n), reverse(f.begin()+1, f.end()), DFT(f, n);
        Z I=1;
        for(int i=1; i<n; i<<=1) I*=(P+1)/2;
        for(int i=0; i<n; ++i) f[i]*=I;
    }
    vector<Z> operator +(const vector<Z> &f, const vector<Z> &g){
        vector<Z> ans=f;
        ans.resize(max(f.size(), g.size()));
        for(int i=0; i<(int)g.size(); ++i) ans[i]+=g[i];
        return ans;
    }
    vector<Z> operator *(const vector<Z> &f, const vector<Z> &g){
        static vector<Z> F, G;
        F=f, G=g;
        int p=Get(f.size()+g.size()-2);
        DFT(F, p), DFT(G, p);
        for(int i=0; i<p; ++i) F[i]*=G[i];
        IDFT(F, p);
        return F.resize(f.size()+g.size()-1), F;
    }
}
using namespace Poly;
int n;
Z fac[N],ifac[N];
void init(int n){
	fac[0]=1;
    for(int i=1;i<=n;++i){
		fac[i]=fac[i-1]*i;
    } 
	ifac[n]=Pow(fac[n]);
    for(int i=n;i;--i){
    	ifac[i-1]=ifac[i]*i;
    }
}
vector<Z>f,a,b,g,h;
void work(int l, int r){//左闭右开 
    if(l+1==r){
        if(l){
            f[l]=h[l-1]*g[l];
            h[l]+=h[l-1]+Z(2)*f[l];
        }
        else{
            f[l]=1;
            h[l]=1;
        }
        //printf("l:%d r:%d h:%d f:%d\n",l,r,h[l].x,f[l].x);
        return;
    }
    int mid=(l+r)>>1,sz=(r-l)>>1;
	work(l,mid); 
    if(l==0){
    	a.resize(r-l);b.resize(sz);
    	memset(&a[sz],0,sizeof(Z)*sz); //把a的右区间强制清0 (2,0)
        memcpy(&a[0],&f[l],sizeof(Z)*sz); //把a的左区间强制赋成f已经算的值 (2,0) 移到a的对应部分 
        memcpy(&b[0],&f[0],sizeof(Z)*sz); //把整个区间长度的g移动到b的位置 
        a=a*b;
        for(int i=sz;i<r-l;i++){//后半段加上左对右的贡献
            //printf("l:%d r:%d i:%d add:%d\n",l,r,i,a[i].x);
            h[l+i]+=a[i];
        }
    }
    else{
        a.resize(r-l);b.resize(r-l);
        memset(&a[sz],0,sizeof(Z)*sz); //把a的右区间强制清0 (2,0)
        memcpy(&a[0],&f[l],sizeof(Z)*sz); //把a的左区间强制赋成f已经算的值 (2,0) 移到a的对应部分 
        memcpy(&b[0],&f[0],sizeof(Z)*(r-l)); //把整个区间长度的g移动到b的位置
        a=a*b;
        for(int i=sz;i<r-l;i++){//后半段加上左对右的贡献
            //printf("l:%d r:%d i:%d add:%d\n",l,r,i,2*a[i].x);
            h[l+i]+=Z(2)*a[i];
        }
    }
	work(mid,r);
}
int main(){
    Init();
    init(N-1);
    scanf("%d",&n);
    int lg=1;
	while((1<<lg)<=n)lg++;
    //printf("lg:%d\n",lg);
	f.resize(1<<lg);f[0].x=1;
	g.resize(1<<lg);g[0].x=0;
    h.resize(1<<lg);h[0].x=0;
	for(int i=1;i<=n;++i){
		scanf("%d",&g[i].x);
	}
	work(0,1<<lg);
	for(int i=1;i<=n;++i){
		printf("%d%c",f[i].x," \n"[i==n]);
	} 	
    return 0;
}

代码2（乱搞）

左对右的贡献的前缀和是每次分治现求的，

反正时间瓶颈是做NTT的过程

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<cmath>
#include<vector>
using namespace std;
#define ll long long
#define ull unsigned ll
const int N = 1<<20, P = 998244353;
const int Primitive_root = 3;
struct Z{
    int x;
    Z(const int _x=0):x(_x){}
    Z operator +(const Z &r)const{ return x+r.x<P?x+r.x:x+r.x-P;}
    Z operator -(const Z &r)const{ return x<r.x?x-r.x+P:x-r.x;}
    Z operator -()const{ return x?P-x:0;}
    Z operator *(const Z &r)const{ return static_cast<ull>(x)*r.x%P;}
    Z operator +=(const Z &r){ return x=x+r.x<P?x+r.x:x+r.x-P, *this;}
    Z operator -=(const Z &r){ return x=x<r.x?x-r.x+P:x-r.x, *this;}
    Z operator *=(const Z &r){ return x=static_cast<ull>(x)*r.x%P, *this;}
    friend Z Pow(Z, int);
    pair<Z,Z> Mul(pair<Z,Z> x, pair<Z,Z> y, Z f)const{
        return make_pair(
            x.first*y.first+x.second*y.second*f,
            x.second*y.first+x.first*y.second
        );
    }
};
Z Pow(Z x, int y=P-2){
    Z ans=1;
    for(; y; y>>=1, x=x*x) if(y&1) ans=ans*x;
    return ans;
}
namespace Poly{
    Z w[N];
    Z Inv[N];
    vector<Z> ans;
    vector<vector<Z> > p;
    ull F[N];
    int Get_root(){
        static int pr[N],cnt;
        int n=P-1,sz=(int)(sqrt(n)),root=-1;
        for(int i=2;i<=sz;++i){if(n%i==0)pr[cnt++]=i;while(n%i==0)n/=i;}
        if(n>1)pr[cnt++]=n;
        for(int i=1;i<P;++i){
            if(Pow((Z)i,P-1).x==1){
                bool fl=true;
                for(int j=0;j<cnt;++j){
                    if(Pow(i,(P-1)/pr[j]).x==1){
                        fl=false;break;
                    }
                }
                if(fl){root=i;break;}
            }
        }
        return root;
    }
    void Init(){
        //printf("root:%d\n",Primitive_root=Get_root()); 先求出来原根然后当const用 
        for(int i=1; i<N; i<<=1){
            w[i]=1;
            Z t=Pow((Z)Primitive_root, (P-1)/i/2);
            for(int j=1; j<i; ++j) w[i+j]=w[i+j-1]*t;
        }
        Inv[1]=1;
        for(int i=2; i<N; ++i) Inv[i]=Inv[P%i]*(P-P/i);
    }
    int Get(int x){ int n=1; while(n<=x) n<<=1; return n;}
    int Mod(int x){ return x<P?x:x-P;}
    void DFT(vector<Z> &f, int n){
        if((int)f.size()!=n) f.resize(n);
        for(int i=0, j=0; i<n; ++i){
            F[i]=f[j].x;
            for(int k=n>>1; (j^=k)<k; k>>=1);
        }
        if(n<=4){
            for(int i=1; i<n; i<<=1) for(int j=0; j<n; j+=i<<1){
                Z *W=w+i;
                ull *F0=F+j, *F1=F+j+i;
                for(int k=j; k<j+i; ++k, ++W, ++F0, ++F1){
                    ull t=(*F1)*(W->x)%P;
                    (*F1)=*F0+P-t, (*F0)+=t;
                }
            }
        }
        else{
            for(int j=0; j<n; j+=2){
                int t=F[j+1];
                F[j+1]=Mod(F[j]+P-t), F[j]=Mod(F[j]+t);
            }
            for(int j=0; j<n; j+=4){
                int t0=F[j+2], t1=F[j+3]*w[3].x%P;
                F[j+2]=F[j]+P-t0, F[j]+=t0;
                F[j+3]=F[j+1]+P-t1, F[j+1]+=t1;
            }
            for(int i=4; i<n; i<<=1) for(int j=0; j<n; j+=i<<1){
                Z *W=w+i;
                ull *F0=F+j, *F1=F+j+i;
                for(int k=j; k<j+i; k+=4, W+=4, F0+=4, F1+=4){
                    int t0=(W->x)**F1%P;
                    int t1=(W+1)->x**(F1+1)%P;
                    int t2=(W+2)->x**(F1+2)%P;
                    int t3=(W+3)->x**(F1+3)%P;
                    *F1=*F0+P-t0, *F0+=t0;
                    *(F1+1)=*(F0+1)+P-t1, *(F0+1)+=t1;
                    *(F1+2)=*(F0+2)+P-t2, *(F0+2)+=t2;
                    *(F1+3)=*(F0+3)+P-t3, *(F0+3)+=t3;
                }
            }
        }
        for(int i=0; i<n; ++i) f[i]=F[i]%P;
    }
    void IDFT(vector<Z> &f, int n){
        f.resize(n), reverse(f.begin()+1, f.end()), DFT(f, n);
        Z I=1;
        for(int i=1; i<n; i<<=1) I*=(P+1)/2;
        for(int i=0; i<n; ++i) f[i]*=I;
    }
    vector<Z> operator +(const vector<Z> &f, const vector<Z> &g){
        vector<Z> ans=f;
        ans.resize(max(f.size(), g.size()));
        for(int i=0; i<(int)g.size(); ++i) ans[i]+=g[i];
        return ans;
    }
    vector<Z> operator *(const vector<Z> &f, const vector<Z> &g){
        static vector<Z> F, G;
        F=f, G=g;
        int p=Get(f.size()+g.size()-2);
        DFT(F, p), DFT(G, p);
        for(int i=0; i<p; ++i) F[i]*=G[i];
        IDFT(F, p);
        return F.resize(f.size()+g.size()-1), F;
    }
}
using namespace Poly;
int n;
Z fac[N],ifac[N];
void init(int n){
    fac[0]=1;
    for(int i=1;i<=n;++i){
        fac[i]=fac[i-1]*i;
    } 
    ifac[n]=Pow(fac[n]);
    for(int i=n;i;--i){
        ifac[i-1]=ifac[i]*i;
    }
}
vector<Z>f,a,b,g;
void work(int l, int r){//左闭右开 
    if(l+1==r)return;
    int mid=(l+r)>>1,sz=(r-l)>>1;
    work(l,mid); 
    int up=min(r-l,l);
    //printf("up:%d\n",up);
    if(up){
        a.resize(r-l);b.resize(up);
        memset(&a[sz],0,sizeof(Z)*sz); //把a的右区间强制清0 (2,0)
        memcpy(&a[0],&f[l],sizeof(Z)*sz); //把a的左区间强制赋成f已经算的值 (2,0) 移到a的对应部分 
        memcpy(&b[0],&f[0],sizeof(Z)*up); //把整个区间长度的g移动到b的位置 
        a=a*b; 
        for(int i=1;i<r-l;++i){
            a[i]+=a[i-1];
        }
        for(int i=sz;i<r-l;i++){//后半段加上左对右的贡献
            int w=i-1<0?0:2ll*a[i-1].x%P;
            f[l+i]+=Z(w)*g[l+i];
        }
    }
    a.resize(r-l);b.resize(sz);
    memset(&a[sz],0,sizeof(Z)*sz); //把a的右区间强制清0 (2,0)
    memcpy(&a[0],&f[l],sizeof(Z)*sz); //把a的左区间强制赋成f已经算的值 (2,0) 移到a的对应部分 
    memcpy(&b[0],&f[l],sizeof(Z)*sz); //把整个区间长度的g移动到b的位置
    a=a*b; 
    for(int i=1;i<r-l;++i){
        a[i]+=a[i-1];
    }
    for(int i=sz;i<r-l;i++){//后半段加上左对右的贡献
        int w=i-1-l<0?0:a[i-1-l].x;
        f[l+i]+=Z(w)*g[l+i];
    }
    work(mid,r);
}
int main(){
    Init();
    init(N-1);
    scanf("%d",&n);
    int lg=1;
    while((1<<lg)<=n)lg++;
    //printf("lg:%d\n",lg);
    f.resize(1<<lg);f[0].x=1;
    g.resize(1<<lg);g[0].x=0;
    for(int i=1;i<=n;++i){
        scanf("%d",&g[i].x);
    }
    work(0,1<<lg);
    for(int i=1;i<=n;++i){
        printf("%d%c",f[i].x," \n"[i==n]);
    }   
    return 0;
}