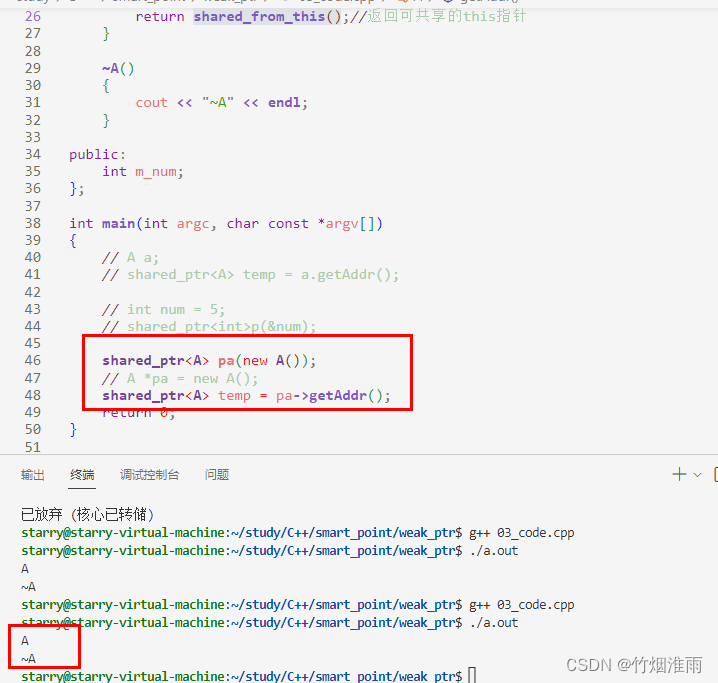
目录
1.算法流程简介
2.算法核心代码
3.算法效果展示
1.算法流程简介
#整数规划模型--匈牙利算法求解
"""
整数规划模型及概念:
规划问题的数学模型一般由三个因素构成 决策变量 目标函数 约束条件;
线性规划即以线性函数为目标函数,线性条件为约束条件;
如果一个线性规划模型中的部分或全部决策变量取整数值,则称该线性规划模型为整数线性规划模型,除此还有非线性整数规划。
整数规划的几种类型:
1:纯整数规划:全部决策变量都必须取整数值的整数规划模型;
2:混合整数规划:决策变量中有一部分必须取整数值,另一部分可以不取整数值的整数规划模型;
3:0-1整数规划:决策变量只能取0或1的整数规划。
匈牙利算法基本思路:
对费用矩阵C的行和列减去某个常数,将C化为有n个位于不同行不同列的零元素,
令这些零元素对应的变量取1,其余变量取0,即得到指派问题的最优解。
匈牙利法是基于指派问题的标准型的,标准型需满足以下3个条件:
(1)目标函数求min;
(2)效率矩阵为n阶方阵;
(3)效率矩阵中所有的元素Cij>=0,且为常数
处理效率矩阵的原则:
匈牙利算法的本质工作就是处理效率矩阵,时期变的符合一定的输入要求
最终效果:效率矩阵通过一定的变换之后,每行每列都至少存在一个0,记这个矩阵为B。
1.如果行列本身就有0,该行列不需要处理
2.如果某行没有0,寻找到该行的min元素,此行都减去min。
3.如果某列没有0,寻找到该列的min元素,此列都减去min。
"""2.算法核心代码
#开始求解整数规划问题
from scipy.optimize import linear_sum_assignment
import numpy as np
#1.导入cost/效率矩阵:
cost_arr=np.array([[4,1,3],
[2,0,5],
[3,2,2]])
n=len(cost_arr)
row_best,col_best=linear_sum_assignment(cost_arr)
print("开销矩阵最优行索引解:",row_best)
print("开销矩阵最优列索引解:",col_best)
#求解最优解:
ans=0
best_ans=[]
for i in range(n):
ans+=cost_arr[row_best[i]][col_best[i]]
best_ans.append(cost_arr[row_best[i]][col_best[i]])
print("最优解由",n,"个数据进行组成")
for i in range(n):
print("第",i+1,"个数据是位于开销矩阵第",row_best[i],"行第",col_best[i],"列的值:",cost_arr[row_best[i]][col_best[i]])
print("综上所示本题最优解组成是:",best_ans)
print("本题规划的最优解是:",ans)3.算法效果展示