文章目录
- 344. 反转字符串
- 1749. 任意子数组和的绝对值的最大值(最大子数组和)
- 1281. 整数的各位积和之差
- 1289. 下降路径最小和 II
- 1572. 矩阵对角线元素的和
- 解法1——加的时候判断
- 解法2——加完之后判断
- 23. 合并 K 个升序链表
- 解法1——使用优先队列合并
- 解法2——分治合并⭐
- 88. 合并两个有序数组
- 解法——逆向双指针
344. 反转字符串
https://leetcode.cn/problems/reverse-string/description/
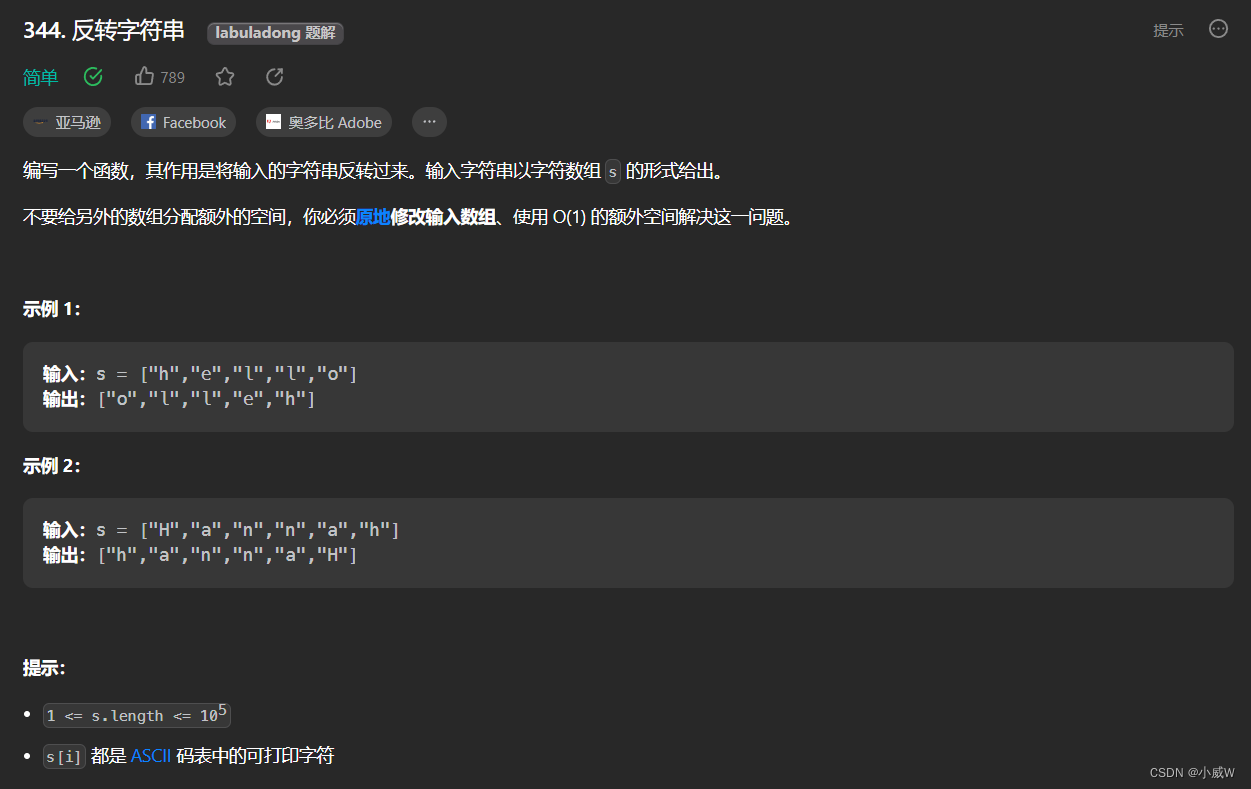
要求原地修改,使用双指针两两交换位置就好了。
class Solution {
public void reverseString(char[] s) {
for (int l = 0, r = s.length - 1; l < r; ++l, --r) {
char t = s[l];
s[l] = s[r];
s[r] = t;
}
}
}
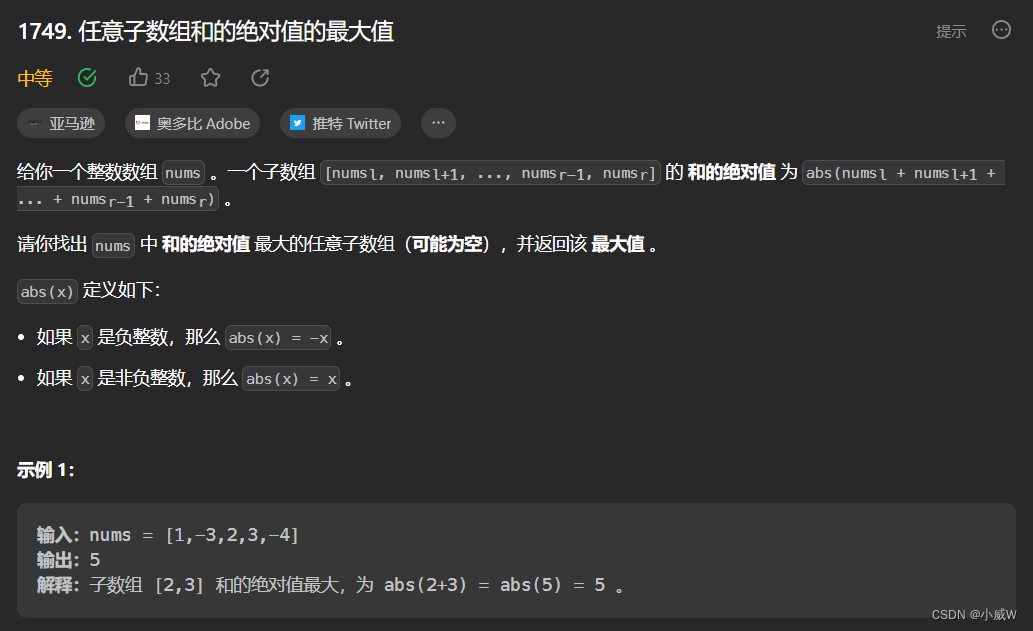
1749. 任意子数组和的绝对值的最大值(最大子数组和)
https://leetcode.cn/problems/maximum-absolute-sum-of-any-subarray/description/
提示:
1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4
参考最大子数组和那道题。
这道题的区别就是维护一个最大值和一个最小值,更新答案时用最大值和最小值取反来更新答案。
class Solution {
public int maxAbsoluteSum(int[] nums) {
int mx = 0, mn = 0, ans = 0;
for (int num: nums) {
mx = mx + num < num? num: mx + num;
mn = mn + num > num? num: mn + num;
ans = Math.max(ans, Math.max(mx, -mn));
}
return ans;
}
}
1281. 整数的各位积和之差
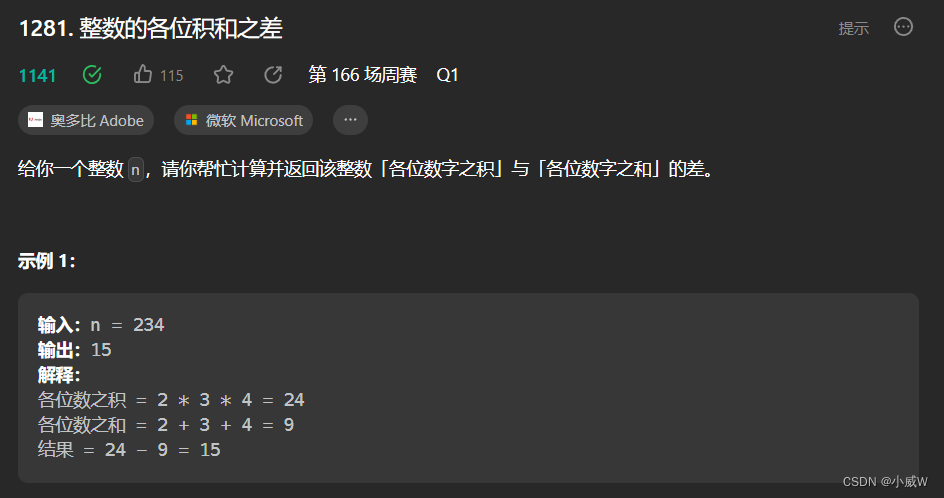
1281. 整数的各位积和之差
提示:
1 <= n <= 10^5
模拟即可。
class Solution {
public int subtractProductAndSum(int n) {
int mul = 1, sum = 0;
while (n != 0) {
int v = n % 10;
n /= 10;
mul *= v;
sum += v;
}
return mul - sum;
}
}
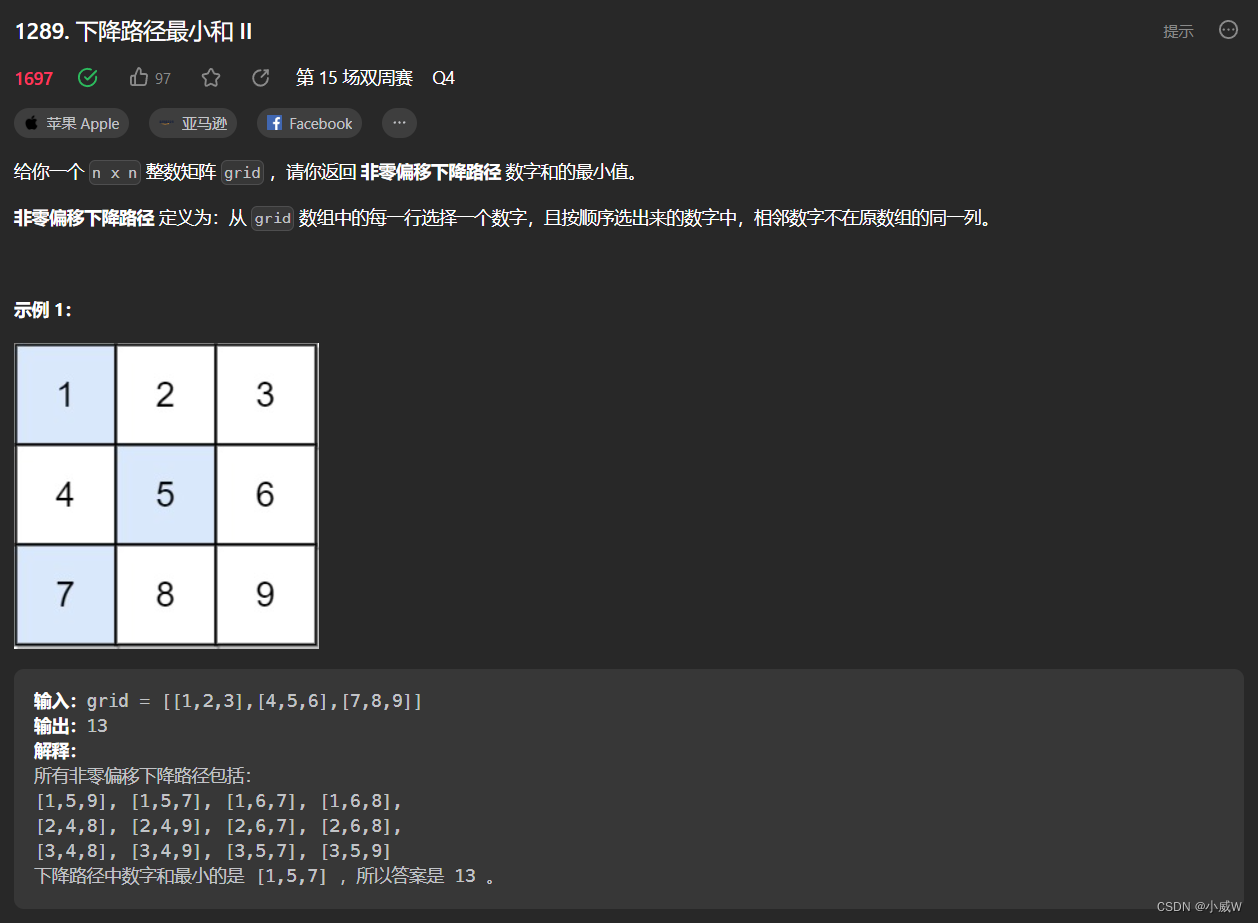
1289. 下降路径最小和 II
https://leetcode.cn/problems/minimum-falling-path-sum-ii/description/
提示:
n == grid.length == grid[i].length
1 <= n <= 200
-99 <= grid[i][j] <= 99
解法1——动态规划 O ( n 3 ) O(n^3) O(n3)
从数据范围来看,可以使用
O
(
n
3
)
O(n^3)
O(n3)的算法。
对于每个位置,选择上一行中最小的那个位置递推过来即可。
class Solution {
public int minFallingPathSum(int[][] grid) {
int m = grid.length, n = grid[0].length;
// 枚举第1~m-1行
for (int i = 1; i < m; ++i) {
// 枚举当前行的0~n-1列
for (int j = 0; j < n; ++j) {
// 枚举上一行的0~n-1列,选出其中最小的
int v = Integer.MAX_VALUE;
for (int k = 0; k < n; ++k) {
if (k != j) v = Math.min(v, grid[i - 1][k]);
}
grid[i][j] += v;
}
}
return Arrays.stream(grid[m - 1]).min().getAsInt();
}
}
解法2——转移过程优化 O ( n 2 ) O(n^2) O(n2) ⭐
在状态转移的过程中可以发现,第 i 行的很多位置是从 i - 1 行的同一列转移过来的,因为他们都会优先选择第 i - 1 行的最小值,只有当列相同时才会去选择次小值。
因此我们只需要维护三个变量:最小值、最小值对应的列、次小值 即可,不需要完整枚举上一行的每一列。
class Solution {
public int minFallingPathSum(int[][] grid) {
int n = grid.length;
int mn = 0, mn2 = 0, mnId = -1;
// 枚举每一行
for (int i = 0; i < n; ++i) {
// 当前行的最小值、次小值、最小值下标
int curMn = Integer.MAX_VALUE, curMn2 = Integer.MAX_VALUE, curMnId = -1;
// 枚举每一列
for (int j = 0; j < n; ++j) {
int curSum = (j != mnId? mn: mn2) + grid[i][j];
// 使用当前和更新最小值和次小值
if (curSum < curMn) {
curMn2 = curMn;
curMn = curSum;
curMnId = j;
} else if (curSum < curMn2) {
curMn2 = curSum;
}
}
// 更新上一行的最小值、次小值、最小值下标
mn = curMn;
mn2 = curMn2;
mnId = curMnId;
}
return mn;
}
}
优化之后,执行用时从 32ms 变成了 1ms。效果显著。
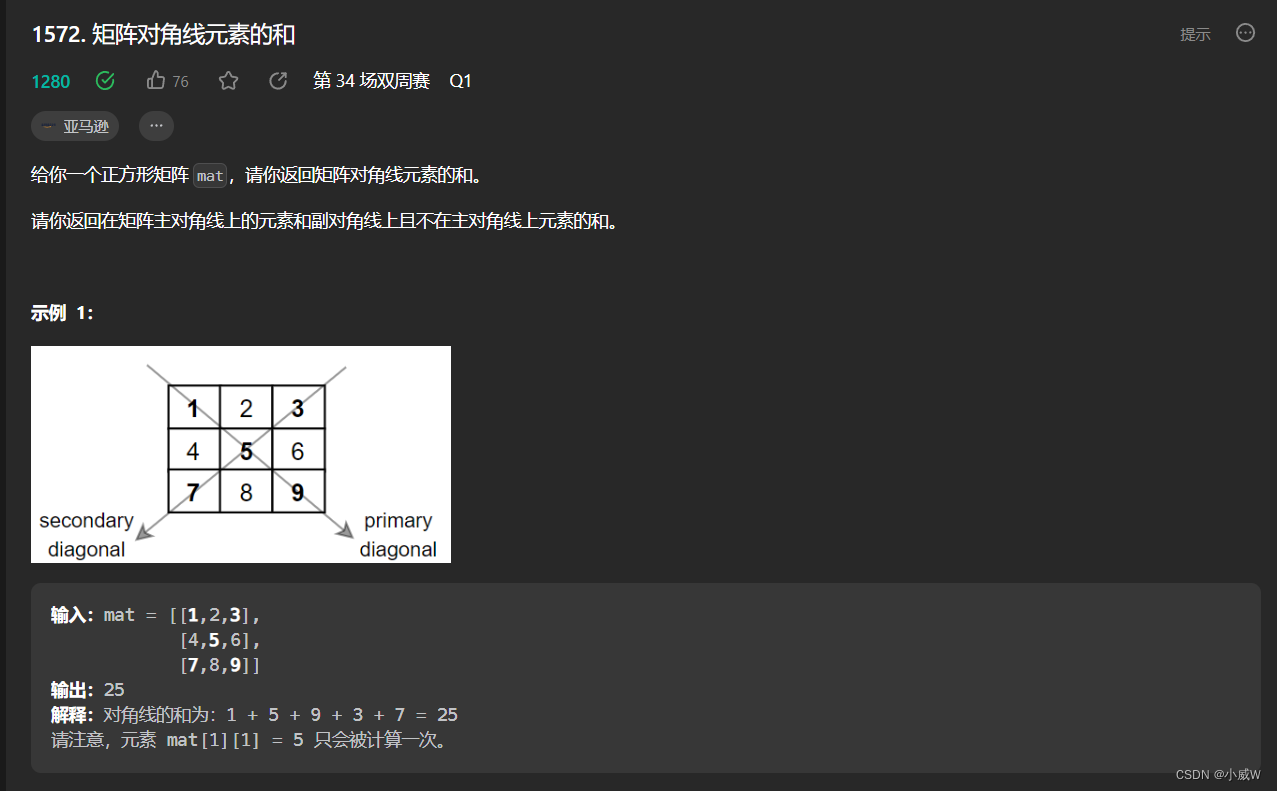
1572. 矩阵对角线元素的和
https://leetcode.cn/problems/matrix-diagonal-sum/
提示:
n == mat.length == mat[i].length
1 <= n <= 100
1 <= mat[i][j] <= 100
解法1——加的时候判断
class Solution {
public int diagonalSum(int[][] mat) {
int n = mat.length, ans = 0;
for (int i = 0; i < n; ++i) {
ans += mat[i][i];
if (n - 1 - i != i) ans += mat[i][n - 1 - i];
}
return ans;
}
}
解法2——加完之后判断
循环里面不用写 if 了,最后判断一下 n 是奇数还是偶数就好了。
class Solution {
public int diagonalSum(int[][] mat) {
int n = mat.length, ans = 0;
for (int i = 0; i < n; ++i) {
ans += mat[i][i] + mat[i][n - 1 - i];
}
return ans - mat[n / 2][n / 2] * (n & 1);
}
}
23. 合并 K 个升序链表
https://leetcode.cn/problems/merge-k-sorted-lists/
提示:
k == lists.length
0 <= k <= 10^4
0 <= lists[i].length <= 500
-10^4 <= lists[i][j] <= 10^4
lists[i] 按 升序 排列
lists[i].length 的总和不超过 10^4
解法1——使用优先队列合并
将 k 个链表放入优先队列中,每次取出最小的,使用后再将其 next 节点放入优先队列即可。
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
PriorityQueue<ListNode> pq = new PriorityQueue<>((a, b) -> a.val - b.val);
for (ListNode list: lists) {
if (list != null) pq.offer(list);
}
ListNode dummy = new ListNode(-1), prev = dummy;
while (!pq.isEmpty()) {
ListNode cur = pq.poll();
prev.next = cur;
prev = cur;
if (cur.next != null) pq.offer(cur.next);
}
return dummy.next;
}
}
解法2——分治合并⭐
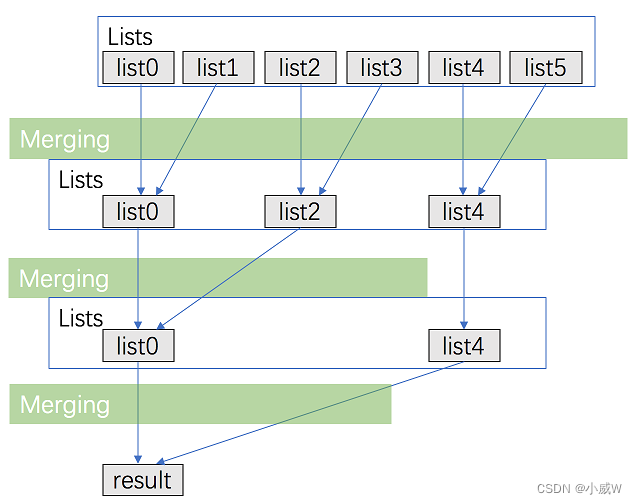
类似于归并排序时使用的思想,两两处理,向上归并。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
return mergeKLists(lists, 0, lists.length);
}
public ListNode mergeKLists(ListNode[] lists, int i, int j) {
int m = j - i; // 这段区间的长度
if (m == 0) return null;
if (m == 1) return lists[i];
// 分成左右两个区间处理
ListNode left = mergeKLists(lists, i, i + m / 2);
ListNode right = mergeKLists(lists, i + m / 2, j);
return mergeTwoLists(left, right);
}
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
ListNode dummy = new ListNode(); // 用哨兵节点简化代码逻辑
ListNode cur = dummy;
while (list1 != null && list2 != null) {
if (list1.val < list2.val) {
cur.next = list1;
list1 = list1.next;
} else {
cur.next = list2;
list2 = list2.next;
}
cur = cur.next;
}
cur.next = list1 != null? list1: list2;
return dummy.next;
}
}
这两种解法的时间复杂度都是 O ( n ∗ log k ) O(n*\log{k}) O(n∗logk)
88. 合并两个有序数组
https://leetcode.cn/problems/merge-sorted-array/
提示:
nums1.length == m + n
nums2.length == n
0 <= m, n <= 200
1 <= m + n <= 200
-10^9 <= nums1[i], nums2[j] <= 10^9
进阶:你可以设计实现一个时间复杂度为 O(m + n) 的算法解决此问题吗?
解法——逆向双指针
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int i = m - 1, j = n - 1, k = m + n - 1;
while (i >= 0 && j >= 0) {
if (nums1[i] >= nums2[j]) nums1[k--] = nums1[i--];
else nums1[k--] = nums2[j--];
}
while (i >= 0) nums1[k--] = nums1[i--];
while (j >= 0) nums1[k--] = nums2[j--];
}
}