文章目录

一：纹理描述
- （1）联合概率矩阵法
- - A：定义
  - B：基于联合概率矩阵的特征
  - C：程序
- （2）灰度差分统计法
- - A：定义
  - B：描述图像特征的参数
- （3）行程长度统计法
- - A：定义
  - B：使用灰度级行程长度的特征
  - C：程序
- （4）LBP特征
- - A：定义
  - B：程序
二：其他描述
- （1）梯度方向直方图
- - A：定义
  - B：程序
- （2）Haar-like特征
- - A：定义
  - B：程序

一：纹理描述

纹理描述：是用于描述三维模型表面外观的技术。它通过应用纹理映射（Texture Mapping）将二维图像或图案映射到三维模型的表面上，从而为模型赋予更加真实、丰富的外观。纹理描述可以包含多种信息，例如颜色、光照、反射、透明度等。通过在模型的顶点或多边形上定义纹理坐标，将纹理映射到相应的位置，可以在渲染过程中使模型显示出纹理的效果。常见的纹理描述格式包括：

位图纹理（Bitmap Texture）：使用常见的图像文件格式（如JPEG、PNG等）作为纹理，可以直接获取真实世界中的照片或图像
矢量纹理（Vector Texture）：使用矢量图形描述的纹理，可以无损缩放和编辑，适用于需要保持良好清晰度的情况
法线贴图（Normal Map）：通过修改模型表面法线的方式，模拟物体表面微小凹凸结构的效果，以增强模型的细节感
凹凸贴图（Bump Map）：通过改变模型表面法线方向的方式，模拟物体表面凹凸结构的效果
环境贴图（Environment Map）：用于模拟物体周围环境的反射和折射效果，增加模型的真实感

（1）联合概率矩阵法

A：定义

联合概率矩阵法：是一种用于数据分析和模式识别的统计方法。它主要用于分析多个变量之间的联合概率分布，并通过构建联合概率矩阵来描述这些变量之间的关系。该方法基于联合概率分布的思想，将多维数据转化为一个二维矩阵，矩阵中的每个元素表示对应变量的联合概率值。通过观察和分析这个矩阵，可以揭示不同变量之间的相关性、依赖性和模式等信息。具体步骤如下

收集样本数据：首先需要收集包含多个变量的样本数据集，例如观测数据或实验数据
构建联合概率矩阵：根据样本数据，计算得到各个变量之间的联合概率矩阵。矩阵的行和列分别代表不同的变量，矩阵中的每个元素表示对应变量取值组合的联合概率
分析矩阵：通过观察和分析联合概率矩阵，可以发现其中的模式、相关性和依赖性等信息。可以采用统计指标、可视化工具或其他分析方法来进一步解读矩阵

具体来说，取图像中点 $(x, y)$ 及偏离它的另一点 $(x+\nabla x,y+\nabla y)$ ，设该点对的灰度值为 $f_{1},f_{2})$ ，令点 $(x, y)$ 在整个画面上移动，得到各种 $f_{1},f_{2})$ 值。设灰度值级数为 $L$ ，则 $f_{1}$ 与 $f_{2}$ 的组合共有 $L^{2}$ 种。对于整个画面，统计出每一种值 $f_{1},f_{2})$ 出现的次数，然后排列成一个方阵，再用 $f_{1},f_{2})$ 出现的总次数将它们归一化为出现的概率 $p(f_{1},f_{2})$ ，称方阵为联合概率矩阵

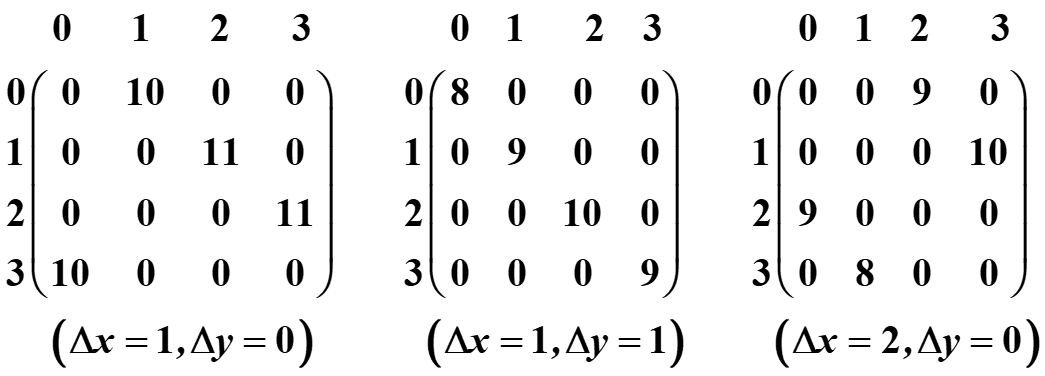
在这里插入图片描述

B：基于联合概率矩阵的特征

角二阶矩：

$M=\sum_{f_{1}} \sum_{f_{2}}\left[p\left(f_{1}, f_{2}\right)\right]^{2}$

相关系数：

$\begin{array}{c}C O R=\frac{\sum_{f_{1}} \sum_{f_{2}}\left(f_{1}-\mu_{f_{1}}\right)\left(f_{2}-\mu_{f_{2}}\right) p\left(f_{1}, f_{2}\right)}{\sigma_{f_{1}} \sigma_{f_{2}}} \\\mu_{f_{1}}=\sum_{f_{1}} f_{1} \sum_{f_{2}} p\left(f_{1}, f_{2}\right) \quad \mu_{f_{2}}=\sum_{f_{2}} f_{2} \sum_{f_{1}} p\left(f_{1}, f_{2}\right) \\\sigma_{f_{1}}^{2}=\sum_{f_{1}}\left(f_{1}-\mu_{f_{1}}\right)^{2} \sum_{f_{2}} p\left(f_{1}, f_{2}\right) \sigma_{f_{2}}^{2}=\sum_{f_{2}}\left(f_{2}-\mu_{f_{2}}\right)^{2} \sum_{f_{1}} p\left(f_{1}, f_{2}\right)\end{array}$

对比度：

$N=\sum_{k} k^{2}\left[\sum_{\substack{f_{1} \\ f_{2} \\ k \in\left|f_{1}-f_{2}\right|}} p\left(f_{1}, f_{2}\right)\right]$

倒数差分矩：

$M=\sum_{f_{1}} \sum_{f_{2}} \frac{p\left(f_{1}, f_{2}\right)}{1+\left|f_{1}-f_{2}\right|}$

熵：

$T=-\sum_{f_{1}} \sum_{f_{2}} p\left(f_{1}, f_{2}\right) \log _{2} p\left(f_{1}, f_{2}\right)$

C：程序

如下，打开一幅灰度图像，生成联合概率矩阵并计算参数。可以发现，平滑后图像对比度降低，自相关性增强，角二阶矩和倒数差分矩增大

在这里插入图片描述

matlab：

clear,clc,close all;
Iorigin=imread('morphplane.jpg');
Iorigin=255-Iorigin;
Irotate=imrotate(Iorigin,15,'bilinear');
Iresize=imresize(Iorigin,0.4,'bilinear');
Imirror=fliplr(Iorigin);

bwo=im2bw(Iorigin);
bwr=im2bw(Irotate);
bws=im2bw(Iresize);
bwm=im2bw(Imirror);

huo=invmoments(bwo);
hur=invmoments(bwr);
hus=invmoments(bws);
hum=invmoments(bwm);   

    
function Hu=invmoments(bw)
[N,M]=size(bw);
M00=0;
M10=0;
M01=0;
for x=1:M
    for y=1:N
        M00=M00+bw(y,x);
        M10=M10+x*bw(y,x);
        M01=M01+y*bw(y,x);
    end
end
centerx=M10/M00;
centery=M01/M00;
u02=0;u20=0;u11=0;u21=0;u12=0;u30=0;u03=0;
for x=1:M
    for y=1:N
        u20=u20+bw(y,x)*(x-centerx)^2;
        u02=u02+bw(y,x)*(y-centery)^2;
        u11=u11+bw(y,x)*(x-centerx)*(y-centery);
        u30=u30+bw(y,x)*(x-centerx)^3;
        u03=u03+bw(y,x)*(y-centery)^3;
        u21=u21+bw(y,x)*(x-centerx)^2*(y-centery);
        u12=u12+bw(y,x)*(y-centery)^2*(x-centerx);
    end
end
n20=u20/(M00^2);n02=u02/(M00^2);n11=u11/(M00^2);
n21=u21/(M00^2.5);n12=u12/(M00^2.5);
n03=u03/(M00^2.5);n30=u30/(M00^2.5);
Hu(1)=n20+n02;
Hu(2)=(n20-n02)^2+4*n11^2;
Hu(3)=(n30-3*n12)^2+(3*n21-n03)^2;
Hu(4)=(n30+n12)^2+(n21+n03)^2;
Hu(5)=(n30-3*n12)*(n30+n12)*((n30+n12)^2-3*(n21+n03)^2)...
    +(3*n21-n03)*(n21+n03)*(3*(n30+n12)^2-(n21+n03)^2);
Hu(6)=(n20-n02)*((n03+n12)^2-(n21+n03)^2)+4*n11*(n30+n12)*(n21+n03);
Hu(7)=(3*n21-n03)*(n30+n12)*((n30+n12)^2-3*(n21+n03)^2)...
    -(n30-3*n12)*(n21+n03)*(3*(n30+n12)^2-(n21+n03)^2);
end

python：

import numpy as np
import matplotlib.pyplot as plt
from PIL import Image

def invmoments(bw):
    N, M = bw.shape
    M00 = np.sum(bw)
    M10 = np.sum(np.multiply(np.arange(M), bw))
    M01 = np.sum(np.multiply(np.arange(N).reshape(N, 1), bw))

    centerx = M10 / M00
    centery = M01 / M00

    u02 = 0
    u20 = 0
    u11 = 0
    u21 = 0
    u12 = 0
    u30 = 0
    u03 = 0

    for x in range(M):
        for y in range(N):
            u20 += bw[y, x] * (x - centerx) ** 2
            u02 += bw[y, x] * (y - centery) ** 2
            u11 += bw[y, x] * (x - centerx) * (y - centery)
            u30 += bw[y, x] * (x - centerx) ** 3
            u03 += bw[y, x] * (y - centery) ** 3
            u21 += bw[y, x] * (x - centerx) ** 2 * (y - centery)
            u12 += bw[y, x] * (y - centery) ** 2 * (x - centerx)

    n20 = u20 / (M00 ** 2)
    n02 = u02 / (M00 ** 2)
    n11 = u11 / (M00 ** 2)
    n21 = u21 / (M00 ** 2.5)
    n12 = u12 / (M00 ** 2.5)
    n03 = u03 / (M00 ** 2.5)
    n30 = u30 / (M00 ** 2.5)

    Hu = np.zeros(7)
    Hu[0] = n20 + n02
    Hu[1] = (n20 - n02) ** 2 + 4 * n11 ** 2
    Hu[2] = (n30 - 3 * n12) ** 2 + (3 * n21 - n03) ** 2
    Hu[3] = (n30 + n12) ** 2 + (n21 + n03) ** 2
    Hu[4] = (n30 - 3 * n12) * (n30 + n12) * ((n30 + n12) ** 2 - 3 * (n21 + n03) ** 2) + \
            (3 * n21 - n03) * (n21 + n03) * (3 * (n30 + n12) ** 2 - (n21 + n03) ** 2)
    Hu[5] = (n20 - n02) * ((n03 + n12) ** 2 - (n21 + n03) ** 2) + \
            4 * n11 * (n30 + n12) * (n21 + n03)
    Hu[6] = (3 * n21 - n03) * (n30 + n12) * ((n30 + n12) ** 2 - 3 * (n21 + n03) ** 2) - \
            (n30 - 3 * n12) * (n21 + n03) * (3 * (n30 + n12) ** 2 - (n21 + n03) ** 2)

    return Hu

Iorigin = np.array(Image.open('morphplane.jpg').convert('L'))
Iorigin = 255 - Iorigin
Irotate = Image.fromarray(Iorigin).rotate(15, resample=Image.BILINEAR)
Iresize = Image.fromarray(Iorigin).resize((int(Iorigin.shape[1] * 0.4), int(Iorigin.shape[0] * 0.4)),
                                         resample=Image.BILINEAR)
Imirror = np.fliplr(Iorigin)

bwo = np.array(Image.fromarray(Iorigin).convert('1'))
bwr = np.array(Irotate.convert('1'))
bws = np.array(Iresize.convert('1'))
bwm = np.array(Image.fromarray(Imirror).convert('1'))

huo = invmoments(bwo)
hur = invmoments(bwr)
hus = invmoments(bws)
hum = invmoments(bwm)

plt.figure(figsize=(12, 4))

plt.subplot(141)
plt.imshow(Iorigin, cmap='gray')
plt.title('Original)

（2）灰度差分统计法

A：定义

灰度差分统计法：是一种用于图像纹理分析的方法，它通过计算图像中像素点之间的灰度差异来描述图像的纹理特征。该方法在图像处理、图像分类和目标识别等领域得到广泛应用。具体步骤如下

确定窗口大小：首先需要确定一个窗口大小，窗口的大小会影响到计算结果的精度和计算量
计算灰度差分矩阵：对于图像中的每个像素点，根据其周围窗口内像素的灰度值，计算其与邻近像素之间的差异。常用的差分方式有水平方向差分、垂直方向差分、对角线方向差分等
统计灰度差分矩阵：统计灰度差分矩阵中每个灰度差分值出现的频次或概率，得到灰度差分统计直方图
提取纹理特征：根据灰度差分统计直方图，可以提取出一系列纹理特征，如均值、方差、能量、对比度、相关性等
分类和识别：使用提取的纹理特征进行分类和识别任务，常见的方法包括支持向量机（SVM）、人工神经网络（ANN）等

B：描述图像特征的参数

对比度：

$N=\sum_{i} i^{2} p_{g}(i)$

角度方向二阶矩：

$M=\sum\left[p_{g}(i)\right]^{2}$

熵：

$T=-\sum_{i} p_{g}(i) \lg p_{g}(i)$

平均值：

$N=\frac{1}{m} \sum_{i} i p_{g}(i)$

（3）行程长度统计法

A：定义

行程长度统计法：是一种常用的无损数据压缩算法，也可以用于图像处理中的纹理特征分析。在行程长度统计法中，将连续出现的相同像素值序列进行编码，以减少数据存储空间或传输带宽。具体步骤如下

数据扫描：对图像进行逐行或逐列扫描，记录每次遇到像素值改变的位置
行程长度编码：根据像素值改变的位置，对连续的像素值序列进行编码，记录每个连续序列的起始位置和长度
编码结果存储：将编码结果按照一定的格式存储，通常是使用一个二维数组或列表来保存每个连续序列的起始位置和长度
解码过程：根据编码结果进行解码，通过重建连续的像素值序列来还原原始图像

例如下图，4个灰度级，对于2个方向(0°,45°)，定义相应的行程长度矩阵 $M_{RL}$

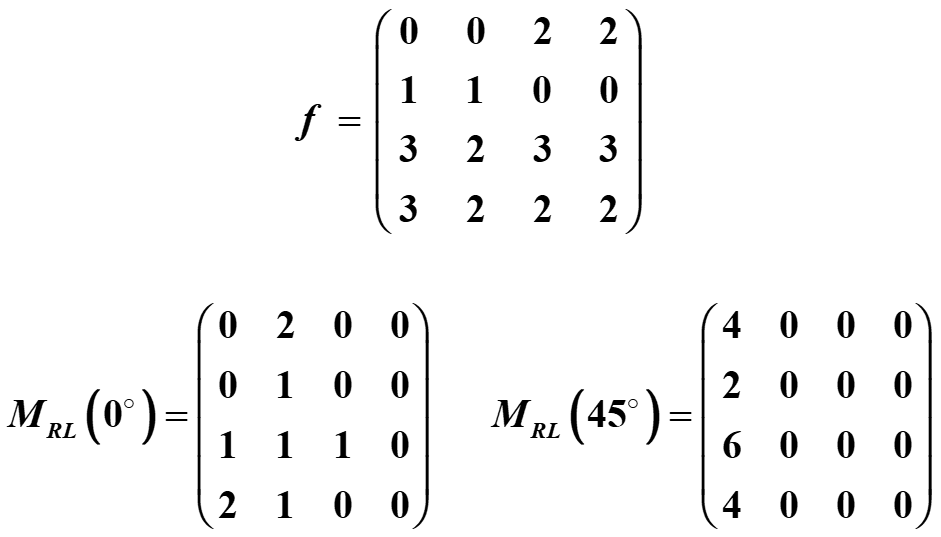
在这里插入图片描述

B：使用灰度级行程长度的特征

短行程补偿：

$E=\frac{\sum_{f} \sum_{n}\left(\frac{M_{R L}(f, n)}{n^{2}}\right)}{\sum_{f} \sum_{n} M_{R L}(f, n)}$

长行程补偿：

$E=\frac{\sum_{f} \sum_{n}\left(M_{R L}(f, n) n^{2}\right)}{\sum_{f} \sum_{n} M_{R L}(f, n)}$

灰度级非均匀性：

$D=\frac{\sum_{f}\left[\sum_{n}\left(M_{R L}(f, n)\right)\right]^{2}}{\sum_{f} \sum_{n} M_{R L}(f, n)}$

行程长度非均匀性：

$D=\frac{\sum_{n}\left[\sum_{f}\left(M_{R L}(f, n)\right)\right]^{2}}{\sum_{f} \sum_{n} M_{R L}(f, n)}$

行程百分比：

$P=\frac{\sum_{f} \sum_{n} M_{R L}(f, n)}{N}$

C：程序

如下，编程计算树皮图像45°方向行程长度矩阵及参数

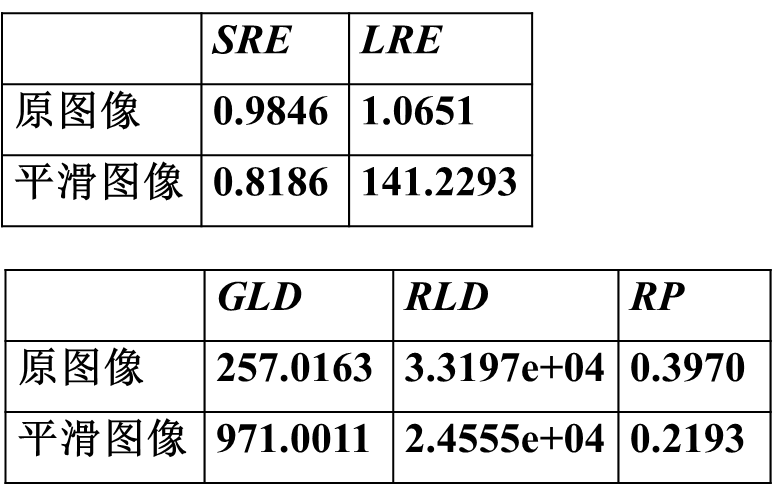
在这里插入图片描述

matlab：

% f=[0 1 2 3 0 1 2;1 2 3 0 1 2 3;2 3 0 1 2 3 0;3 0 1 2 3 0 1;0 1 2 3 0 1 2;1 2 3 0 1 2 3;2 3 0 1 2 3 0];
% f=[0 1 2 3 0 1 2;1 2 3 0 1 2 3;2 3 0 1 2 3 0;3 0 1 2 3 0 1];
% f=[0 1 2 3; 1 2 3 0 ;2 3 0 1 ;3 0 1 2;0 1 2 3;1 2 3 0;2 3 0 1];
f=rgb2gray(imread('texture1.bmp'));
% f=rgb2gray(imread('smoothtexture.jpg'));
f=f+1;
top=max(f(:));
[h,w]=size(f);
N=min(h,w);
MRL=zeros(top,N);
length=1;
for x=1:w
    newx=x;
    newy=1;
    for y=1:min(h,x)
        oldx=newx;
        oldy=newy;
        newx=newx-1;
        newy=y+1;
        if newx>0 && newy<=h && f(newy,newx)==f(oldy,oldx)
            length=length+1;
        else
            MRL(f(oldy,oldx),length)=MRL(f(oldy,oldx),length)+1;
            length=1;
        end
    end
end
for y=2:h
    newx=w;
    newy=y;
    for x=w:-1:1
        oldx=newx;
        oldy=newy;
        newx=x-1;
        newy=oldy+1;
        if newx>0 && newy<=h && f(newy,newx)==f(oldy,oldx)
            length=length+1;
        else
            MRL(f(oldy,oldx),length)=MRL(f(oldy,oldx),length)+1;
            length=1;
            break;
        end
    end
end
SRE=0;LRE=0;GLD=0;RLD=0;RP=0;total=0;GLDp=0;
for n=1:N
    RLDp=0;    
    for f=1:top
        if MRL(f,n)~=0
            total=total+MRL(f,n);
            SRE=SRE+MRL(f,n)/(n^2);
            LRE=LRE+MRL(f,n)*(n^2);
            RLDp=RLDp+MRL(f,n);
            RP=RP+MRL(f,n);
        end
    end
    RLD=RLD+RLDp^2;
end
for f=1:top
    GLDp=0;
    for n=1:N
        if MRL(f,n)~=0
            GLDp=GLDp+MRL(f,n);
        end
    end
    GLD=GLD+GLDp^2;
end
SRE=SRE/total;
LRE=LRE/total;
RLD=RLD/total;
RP=RP/(h*w);
GLD=GLD/total;

python：

import numpy as np
from PIL import Image
import matplotlib.pyplot as plt

# 读取图像
image = Image.open('morphplane.jpg')
Iorigin = np.array(image)

# 转换为灰度图像
f = np.array(image.convert('L'))

f = f + 1
top = np.max(f)
h, w = f.shape
N = min(h, w)
MRL = np.zeros((top, N))
length = 1

for x in range(w):
    newx = x
    newy = 0
    for y in range(min(h, x+1)):
        oldx = newx
        oldy = newy
        newx -= 1
        newy += 1
        if newx >= 0 and newy < h and f[newy, newx] == f[oldy, oldx]:
            length += 1
        else:
            MRL[f[oldy, oldx], length] += 1
            length = 1

for y in range(1, h):
    newx = w
    newy = y
    for x in range(w-1, -1, -1):
        oldx = newx
        oldy = newy
        newx -= 1
        newy += 1
        if newx >= 0 and newy < h and f[newy, newx] == f[oldy, oldx]:
            length += 1
        else:
            MRL[f[oldy, oldx], length] += 1
            length = 1
            break

SRE = 0
LRE = 0
GLD = 0
RLD = 0
RP = 0
total = 0
GLDp = 0

for n in range(N):
    RLDp = 0
    for i in range(1, top+1):
        if MRL[i, n] != 0:
            total += MRL[i, n]
            SRE += MRL[i, n] / (n**2)
            LRE += MRL[i, n] * (n**2)
            RLDp += MRL[i, n]
            RP += MRL[i, n]
    RLD += RLDp**2

for i in range(1, top+1):
    GLDp = 0
    for n in range(N):
        if MRL[i, n] != 0:
            GLDp += MRL[i, n]
    GLD += GLDp**2

SRE /= total
LRE /= total
RLD /= total
RP /= (h * w)
GLD /= total

# 图像展示部分
plt.subplot(121)
plt.imshow(Iorigin)
plt.title('Original Image')
plt.axis('off')

plt.subplot(122)
plt.imshow(f, cmap='gray')
plt.title('Grayscale Image')
plt.axis('off')

plt.show()

（4）LBP特征

A：定义

LBP特征：是一种用于图像纹理描述和特征提取的方法。它在图像的每个像素点上定义了一个局部邻域，并将该邻域中的像素与中心像素进行比较，根据比较结果生成一个二进制编码。LBP特征可以捕捉到图像中不同纹理模式的出现频率和分布情况。计算步骤如下

选择一个像素点作为中心像素
确定一个以中心像素为中心的邻域区域，通常是以中心像素为中心的正方形或圆形区域
比较邻域内的每个像素与中心像素的灰度值大小。如果像素值大于等于中心像素的灰度值，则该位置标记为1，否则标记为0。
将二进制编码转换为十进制数，得到该中心像素的LBP值
遍历图像的每个像素重复步骤1-4，计算得到整张图像的LBP特征

通过LBP特征的提取，我们可以获得以下信息

纹理模式：LBP特征可以描述图像中的不同纹理模式，例如平滑、粗糙、细腻等。
纹理结构：LBP特征可以反映图像中纹理的分布和排列方式，例如网格状、斑点状等。
纹理统计量：通过统计LBP值在整个图像或局部区域中的出现频率和分布情况，可以得到一些纹理统计量，如直方图、均值、方差等

LBP特征具有以下优点

简单有效：LBP特征的计算简单快速，并且对于图像的光照变化和噪声具有较强的鲁棒性。
不依赖颜色信息：LBP特征仅使用灰度值进行计算，不受颜色变化的影响，适用于彩色和灰度图像。
适用广泛：LBP特征可应用于各种应用领域，如图像分类、纹理识别、人脸识别、行人检测等

B：程序

如下，计算下面图像的LBP特征图

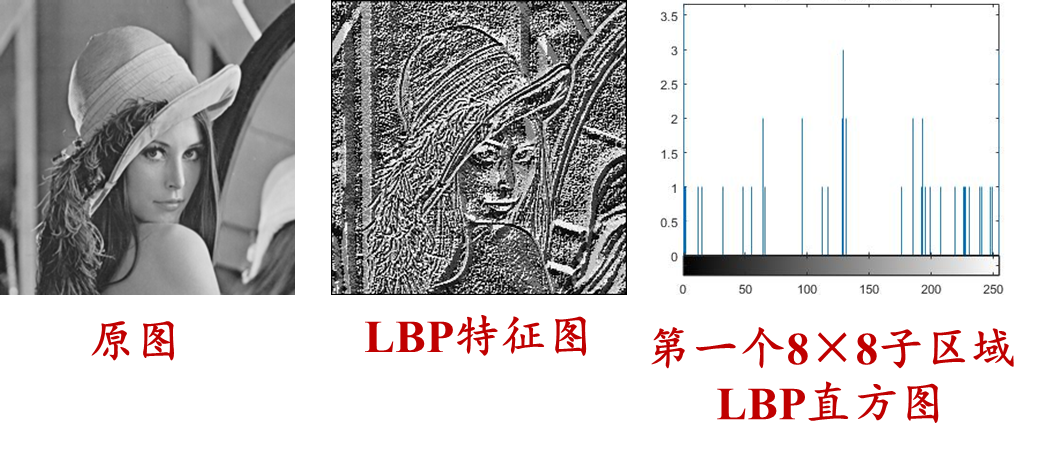
在这里插入图片描述

matlab：

clear,clc,close all;
image=imread('lena.bmp');
[N,M]=size(image);
lbp=zeros(N,M);
for j=2:N-1
    for i=2:M-1
        neighbor=[j-1 i-1;j-1 i;j-1 i+1;j i+1;j+1 i+1;j+1 i;j+1 i-1;j i-1];
        count=0;
        for k=1:8
            if image(neighbor(k,1),neighbor(k,2))>image(j,i)
                count=count+2^(8-k);
            end
        end
        lbp(j,i)=count;
    end
end
lbp=uint8(lbp);
figure,imshow(lbp),title('LBP特征图');
% imwrite(lbp,'lenalbp.jpg');
subim=lbp(1:8,1:8);
imhist(subim),title('第一个子区域直方图');

python：

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像
image = cv2.imread('lena.bmp', 0)

N, M = image.shape
lbp = np.zeros((N, M), dtype=np.uint8)

for j in range(1, N-1):
    for i in range(1, M-1):
        neighbor = [
            [j-1, i-1], [j-1, i], [j-1, i+1],
            [j, i+1], [j+1, i+1], [j+1, i],
            [j+1, i-1], [j, i-1]
        ]
        count = 0
        for k in range(8):
            if image[neighbor[k][0], neighbor[k][1]] > image[j, i]:
                count += 2 ** (7 - k)
        lbp[j, i] = count

plt.imshow(lbp, cmap='gray')
plt.title('LBP特征图')
plt.axis('off')
plt.show()

subim = lbp[:8, :8]
plt.hist(subim.flatten(), bins=256, range=[0, 256])
plt.title('第一个子区域直方图')
plt.show()

二：其他描述

（1）梯度方向直方图

A：定义

梯度防线直方图：是一种用于图像特征描述的方法，主要用于图像分类、物体识别和目标检测等计算机视觉任务中。它通过计算图像中每个像素点的梯度方向，并统计梯度方向的分布情况，构建一个直方图来表示图像的特征。计算步骤如下

将图像转换为灰度图像（如果不是灰度图像）
对图像进行平滑处理，如使用高斯滤波器，以降低噪声的影响
计算每个像素点的水平（x方向）和垂直（y方向）梯度。可以使用Sobel、Prewitt等算子进行梯度计算
对每个像素点，根据其水平和垂直梯度计算梯度幅值和梯度方向
将图像划分为若干个区域或块，对每个区域内的像素点进行梯度方向的统计
根据统计结果构建梯度方向直方图。一般将梯度方向空间划分为固定的几个角度范围，例如0°~180°之间划分为8个区间
将每个区域内的梯度方向数目作为直方图的值，得到最终的梯度方向直方图

梯度方向直方图能够提取图像中的边缘和纹理信息，并对这些信息进行编码和表示。通过统计不同梯度方向的分布情况，可以描述图像的结构和纹理特征。在图像分类和物体识别任务中，通常会将梯度方向直方图作为图像特征，然后使用机器学习算法进行训练和分类。它有以下优点

不受光照变化的影响：梯度方向直方图只依赖于像素的梯度信息，而不受光照变化的影响
对局部变化敏感：梯度方向直方图统计了局部区域内的梯度方向分布情况，因此对于局部纹理特征的检测非常敏感
特征维度可控：通过调整划分梯度方向空间的区间数目，可以控制梯度方向直方图的特征维度，以适应不同任务的需求

B：程序

如下，统计图像的HOG特征

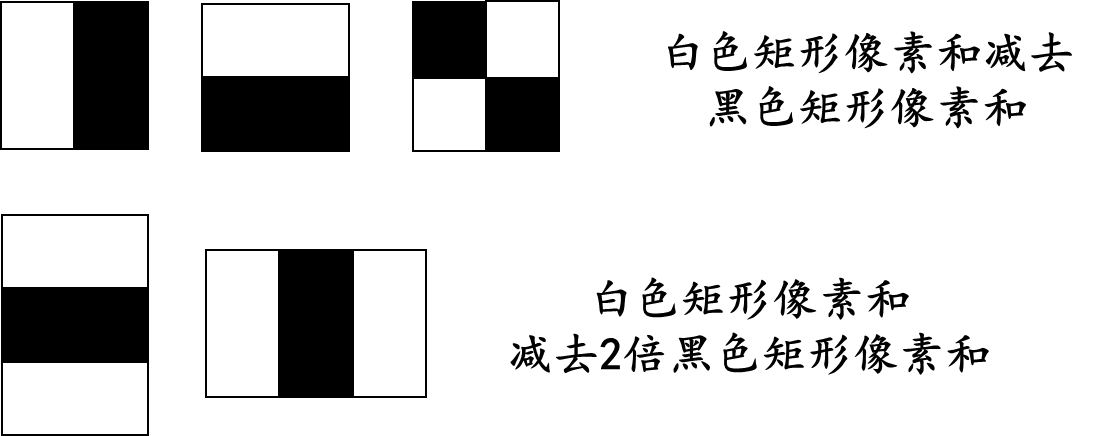
在这里插入图片描述

matlab：

clear,clc,close all;
Image=double(imread('lena.bmp'));
[N,M]=size(Image);
Image=sqrt(Image);
Hy=[-1 0 1];       
Hx=Hy';            
Gy=imfilter(Image,Hy,'replicate');    
Gx=imfilter(Image,Hx,'replicate');   
Grad=sqrt(Gx.^2+Gy.^2);             
Phase=zeros(N,M);   
Eps=0.0001;
for i=1:M
     for j=1:N 
         if abs(Gx(j,i))<Eps && abs(Gy(j,i))<Eps  
             Phase(j,i)=270;
         elseif abs(Gx(j,i))<Eps && abs(Gy(j,i))>Eps 
             Phase(j,i)=90;
         else
             Phase(j,i)=atan(Gy(j,i)/Gx(j,i))*180/pi; 
             if Phase(j,i)<0                                        
                 Phase(j,i)=Phase(j,i)+180; 
             end             
         end
     end
end
step=8;               
K=9;               
angle=180/K;       
Cell=cell(1,1);              
Celli=1;                      
Cellj=1;
for i=1:step:M         
    Cellj=1;
    for j=1:step:N     
        Gtmp=Grad(j:j+step-1,i:i+step-1);
        Gtmp=Gtmp/sum(sum(Gtmp));       
        Hist=zeros(1,K);              
        for x=1:step
            for y=1:step
                ang=Phase(j+y-1,i+x-1); 
                if ang<=180
                    Hist(floor(ang/angle)+1)=Hist(floor(ang/angle)+1)+Gtmp(y,x);   
                end
            end
        end
        Cell{Cellj,Celli}=Hist;      
        Cellj=Cellj+1;               
    end
    Celli=Celli+1;                   
end

[CellN,CellM]=size(Cell);
feature=cell(1,(CellM-1)*(CellN-1));
for i=1:CellM-1
   for j=1:CellN-1           
        f=[];
        f=[f Cell{j,i}(:)' Cell{j,i+1}(:)' Cell{j+1,i}(:)' Cell{j+1,i+1}(:)'];
        f=f./sum(f);
        feature{(i-1)*(CellN-1)+j}=f;
   end
end

python：

clear,clc,close all;
Image=double(imread('lena.bmp'));
[N,M]=size(Image);
Image=sqrt(Image);
Hy=[-1 0 1];       
Hx=Hy';            
Gy=imfilter(Image,Hy,'replicate');    
Gx=imfilter(Image,Hx,'replicate');   
Grad=sqrt(Gx.^2+Gy.^2);             
Phase=zeros(N,M);   
Eps=0.0001;
for i=1:M
     for j=1:N 
         if abs(Gx(j,i))<Eps && abs(Gy(j,i))<Eps  
             Phase(j,i)=270;
         elseif abs(Gx(j,i))<Eps && abs(Gy(j,i))>Eps 
             Phase(j,i)=90;
         else
             Phase(j,i)=atan(Gy(j,i)/Gx(j,i))*180/pi; 
             if Phase(j,i)<0                                        
                 Phase(j,i)=Phase(j,i)+180; 
             end             
         end
     end
end
step=8;               
K=9;               
angle=180/K;       
Cell=cell(1,1);              
Celli=1;                      
Cellj=1;
for i=1:step:M         
    Cellj=1;
    for j=1:step:N     
        Gtmp=Grad(j:j+step-1,i:i+step-1);
        Gtmp=Gtmp/sum(sum(Gtmp));       
        Hist=zeros(1,K);              
        for x=1:step
            for y=1:step
                ang=Phase(j+y-1,i+x-1); 
                if ang<=180
                    Hist(floor(ang/angle)+1)=Hist(floor(ang/angle)+1)+Gtmp(y,x);   
                end
            end
        end
        Cell{Cellj,Celli}=Hist;      
        Cellj=Cellj+1;               
    end
    Celli=Celli+1;                   
end

[CellN,CellM]=size(Cell);
feature=cell(1,(CellM-1)*(CellN-1));
for i=1:CellM-1
   for j=1:CellN-1           
        f=[];
        f=[f Cell{j,i}(:)' Cell{j,i+1}(:)' Cell{j+1,i}(:)' Cell{j+1,i+1}(:)'];
        f=f./sum(f);
        feature{(i-1)*(CellN-1)+j}=f;
   end
end

（2）Haar-like特征

A：定义

Haar-like特征：是一种用于图像分类和目标检测的特征描述方法，最早在Viola-Jones人脸检测算法中被提出并得到广泛应用。它是基于图像的灰度值差异来表示局部图像区域的特征。计算步骤如下

定义一个矩形的模板，该矩形可以是水平、垂直或对角线方向上的连续区域。
将模板放置在图像的不同位置和尺度上，并计算模板内白色（高亮）和黑色（阴影）区域的灰度值之差。
根据灰度值差异计算特征值。常见的Haar-like特征包括：两个相邻矩形的差异、三个相邻矩形的和等等

Haar-like特征的主要思想是通过计算不同矩形区域的灰度值差异来捕捉图像中的局部纹理和边缘信息。具体而言，亮区域和暗区域的灰度值差异可用于表示图像中的边缘，而相邻区域的灰度值差异可用于表示图像中的纹理。其优点如下

简单：Haar-like特征计算简单且高效，适合用于实时应用。
平移不变性：Haar-like特征对图像的平移具有不变性，即特征在图像中的任意位置都能够检测到相同的模式。
多尺度适应性：Haar-like特征可以通过改变模板的尺寸来适应不同大小的目标

其缺点如下

局限性：Haar-like特征主要适用于描述边缘和纹理等低级视觉特征，对于复杂的形状和纹理结构难以有效表示。
不变性差：Haar-like特征对于光照、旋转和尺度变化等因素的不变性较差

B：程序

如下

在这里插入图片描述

matlab：

clear,clc,close all;
Image=double(imread('carphone.jpg'));
[N,M]=size(Image);
win=24;

python：

import cv2
import matplotlib.pyplot as plt

# Read image
image = cv2.imread('carphone.jpg', cv2.IMREAD_GRAYSCALE)
image = image.astype(float)

# Get image size
N, M = image.shape

# Define window size
win = 24

# Display image
plt.imshow(image, cmap='gray')
plt.axis('off')
plt.show()