简单入门--无约束模型预测控制
- 一、模型预测控制是什么?
- 二、无约束线性模型预测控制
- 1. 表达式
- 2. 最优解推导
- 3.MATLAB代码
导读:下棋有高手和菜鸟,高手往往预测未来多步棋局发展,提前布局,而菜鸟只根据当前棋局做选择,显然前瞻不够。模型预测控制有相似的思想。根据当前棋局形势(即系统当前状态)和可能的棋局走势(基于模型预测未来发展),为赢得棋局(根据期望目标),根据自己的经验得出未来多步最优的下棋方案(根据优化方法得出多步最优策略),选择得出的多步最优策略的第一步作为当前步最优决策。并且每次下棋之前都重复上步骤做出最优决策。
一、模型预测控制是什么?
模型预测控制:
1)基于当前系统状态及模型预测系统未来走向
2)根据期望目标,通过优化的方法得出当前及未来多步最优策略
3)将得出的多步最优策略中的第一步作为当前最优决策。
4)每步决策之前,重复上述方案,随时间逐步推进。
因此模型预测控制也成后退时域控制。
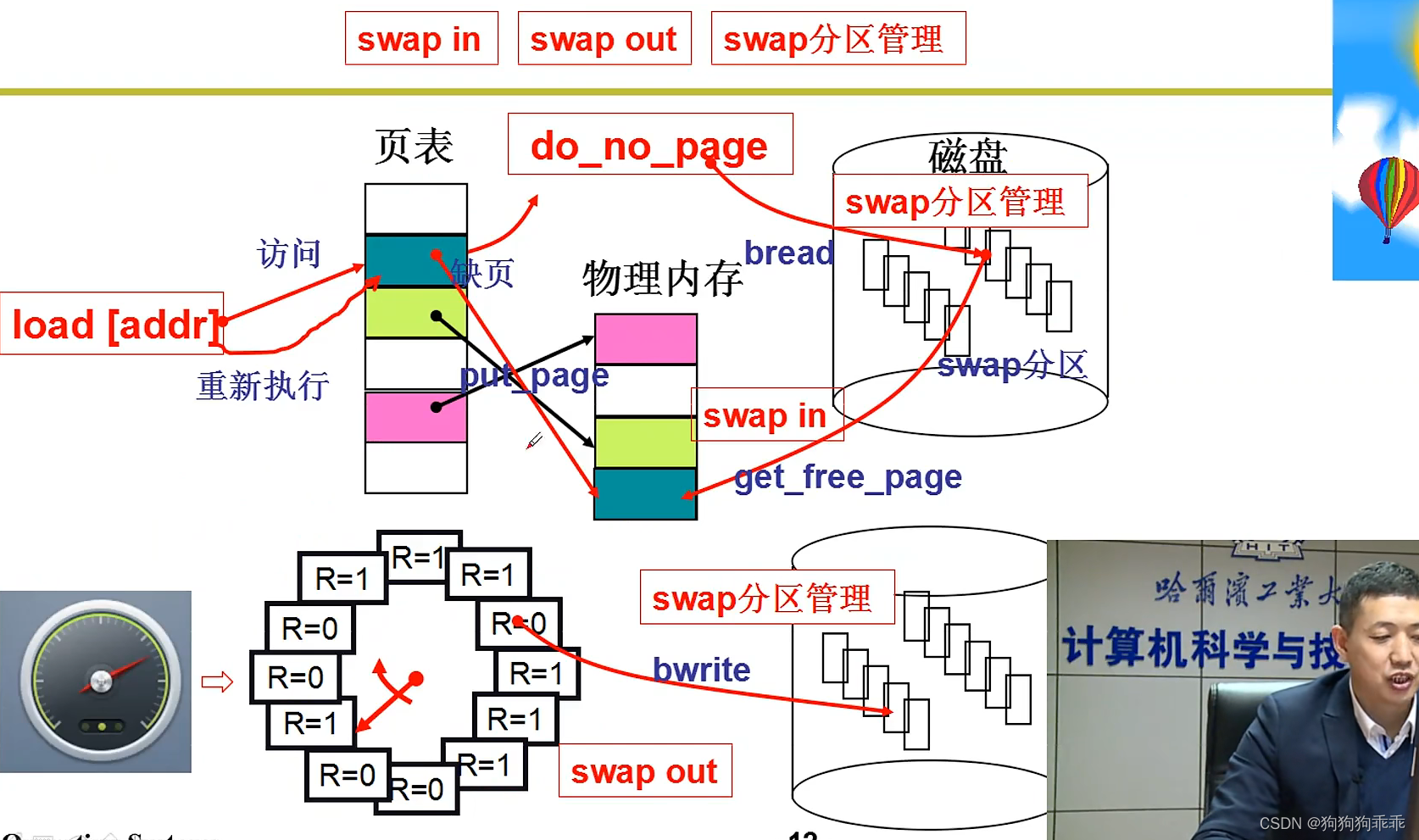
其基本思想如下图
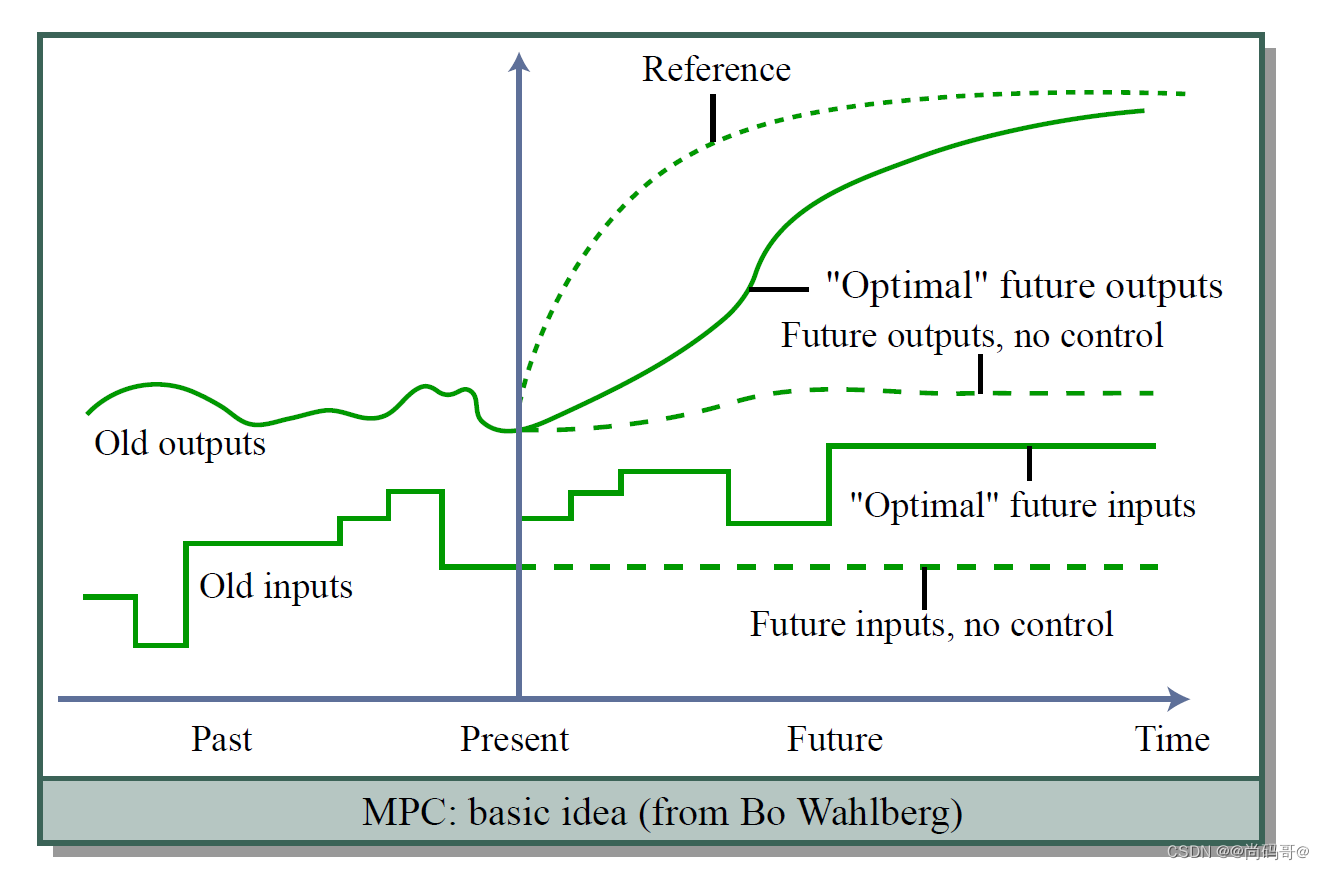
其基本表达式如下:
min
u
J
≜
F
(
x
N
)
+
∑
i
=
0
N
−
1
L
(
x
k
+
i
∣
k
,
u
k
+
i
∣
k
)
目标函数
s.t.:
x
k
+
i
+
1
∣
k
=
f
(
x
k
+
i
∣
k
,
u
k
+
i
∣
k
)
系统模型
x
k
+
i
∣
k
∈
X
状态约束
u
k
+
i
∣
k
∈
U
控制约束
x
k
∣
k
=
x
k
当前系统状态
u
=
[
u
k
∣
k
,
…
,
u
k
+
i
∣
k
,
…
,
u
k
+
N
−
1
∣
k
]
⊤
待优化的控制策略
\begin{aligned} &\mathop{\min}_{u}&& \begin{aligned}J\triangleq F(x_N)+\sum_{i=0}^{N-1}L(x_{k+i|k},u_{k+i|k})\end{aligned} &&目标函数 \\ &\text{s.t.:}&& x_{k+i+1|k}=f(x_{k+i|k},u_{k+i|k}) &&系统模型\\ &&&x_{k+i|k}\in\mathcal{X}&&状态约束\\ &&&u_{k+i|k}\in\mathcal{U}&&控制约束\\ &&& x_{k|k}=x_{k}&&当前系统状态\\ &&& u = \left [ u_{k|k},\dots,u_{k+i|k},\dots,u_{k+N-1|k} \right ] ^\top&&待优化的控制策略 \end{aligned}
minus.t.:J≜F(xN)+i=0∑N−1L(xk+i∣k,uk+i∣k)xk+i+1∣k=f(xk+i∣k,uk+i∣k)xk+i∣k∈Xuk+i∣k∈Uxk∣k=xku=[uk∣k,…,uk+i∣k,…,uk+N−1∣k]⊤目标函数系统模型状态约束控制约束当前系统状态待优化的控制策略
二、无约束线性模型预测控制
当系统模型为线性,即 x k + 1 = A x k + B u k x_{k+1}=Ax_{k}+Bu_{k} xk+1=Axk+Buk, 且无状态约束和控制约束的模型预测控制为无约束线性模型预测控制。
1. 表达式
min
u
J
≜
F
(
x
N
)
+
∑
i
=
0
N
−
1
L
(
x
k
+
i
∣
k
,
u
k
+
i
∣
k
)
目标函数
s.t.:
x
k
+
i
+
1
∣
k
=
A
x
k
+
i
∣
k
+
B
u
k
+
i
∣
k
系统模型
x
k
∣
k
=
x
k
当前系统状态
u
=
[
u
k
∣
k
,
…
,
u
k
+
i
∣
k
,
…
,
u
k
+
N
−
1
∣
k
]
⊤
待优化的控制策略
\begin{aligned} &\mathop{\min}_{u}&& \begin{aligned}J\triangleq F(x_N)+\sum_{i=0}^{N-1}L(x_{k+i|k},u_{k+i|k})\end{aligned} &&目标函数 \\ &\text{s.t.:}&& x_{k+i+1|k}=Ax_{k+i|k}+Bu_{k+i|k} &&系统模型\\ &&& x_{k|k}=x_{k}&&当前系统状态\\ &&& u = \left [ u_{k|k},\dots,u_{k+i|k},\dots,u_{k+N-1|k} \right ] ^\top&&待优化的控制策略 \end{aligned}
minus.t.:J≜F(xN)+i=0∑N−1L(xk+i∣k,uk+i∣k)xk+i+1∣k=Axk+i∣k+Buk+i∣kxk∣k=xku=[uk∣k,…,uk+i∣k,…,uk+N−1∣k]⊤目标函数系统模型当前系统状态待优化的控制策略
这里目标函数通常选为
J
≜
x
k
+
N
∣
k
⊤
Q
N
x
k
+
N
∣
k
+
∑
i
=
0
N
−
1
(
x
k
+
i
∣
k
⊤
Q
x
k
+
i
∣
k
+
u
k
+
i
∣
k
⊤
R
u
k
+
i
∣
k
)
J\triangleq x_{k+N|k}^\top{Q}_Nx_{k+N|k}+\sum_{i=0}^{N-1}\left(x_{k+i|k}^\top{Q}x_{k+i|k}+u_{k+i|k}^\top{R}u_{k+i|k}\right)
J≜xk+N∣k⊤QNxk+N∣k+∑i=0N−1(xk+i∣k⊤Qxk+i∣k+uk+i∣k⊤Ruk+i∣k)
2. 最优解推导
1、根据系统的状态方程,我们可以推出以下结论
x
k
+
1
∣
k
=
A
x
k
∣
k
+
B
u
k
∣
k
x
k
+
2
∣
k
=
A
x
k
+
1
∣
k
+
B
u
k
+
1
∣
k
=
A
2
x
k
∣
k
+
A
B
u
k
∣
k
+
B
u
k
+
1
…
x
k
+
N
∣
k
=
A
x
k
+
N
−
1
∣
k
+
B
u
k
+
N
−
1
=
A
N
x
k
+
A
N
−
1
B
u
k
+
…
…
+
A
B
u
k
+
N
−
2
+
B
u
k
+
N
−
1
\begin{aligned}&{x_{k+1|k}=Ax_{k|k}+Bu_{k|k}}\\ &{x_{k+2|k}=Ax_{k+1|k}+Bu_{k+1|k}=A^2x_{k|k}+ABu_{k|k}+Bu_{k+1}}\\ &\dots\\ &x_{k+N|k}={Ax_{k+N-1|k}+Bu_{k+N_-1}=A^{N}x_k+A^{N-1}Bu_k+\ldots\ldots+ABu_{k+N-2}+Bu_{k+N-1}}\end{aligned}
xk+1∣k=Axk∣k+Buk∣kxk+2∣k=Axk+1∣k+Buk+1∣k=A2xk∣k+ABuk∣k+Buk+1…xk+N∣k=Axk+N−1∣k+Buk+N−1=ANxk+AN−1Buk+……+ABuk+N−2+Buk+N−1
2.上述方程可以重写为以下紧凑形式
[ x k ∣ k x k + 1 ∣ k x k + 2 ∣ k ⋯ x k + N ∣ k ] ⏟ x ˉ = [ I A A 2 ⋯ A N ] ⏟ A ˉ x k + [ 0 0 . . . 0 B 0 . . . 0 A B B . . . 0 ⋯ . . . . . . . . . A N − 1 B A N − 2 B . . . B ] [ u k u k + 1 ⋯ ⋯ u k + N − 1 ] \underbrace{\begin{bmatrix}{x_{k|k}}\\{x_{k+1|k}}\\{x_{k+2|k}}\\\cdots\\{x_{k+N|k}}\end{bmatrix}}_{\bar{{x}}}=\underbrace{\begin{bmatrix}{I}\\{A}\\{A^2}\\\cdots\\A^{N}\end{bmatrix}}_{\bar{A}}{x_k}+\begin{bmatrix}{0}&0&...&0\\{B}&0&...&0\\{AB}&{B}&...&0\\\cdots&...&...&...\\{A^{N-1B}}&{A^{N-2}B}&...&{B}\end{bmatrix}\begin{bmatrix}{u_k}\\{u_{k+1}}\\\cdots\\\cdots\\{u_{k+N-1}}\end{bmatrix} xˉ xk∣kxk+1∣kxk+2∣k⋯xk+N∣k =Aˉ IAA2⋯AN xk+ 0BAB⋯AN−1B00B...AN−2B...............000...B ukuk+1⋯⋯uk+N−1
3.MATLAB代码
代码如下(示例):
A = B
该处使用的url网络请求的数据。