文章目录

一、并查集是什么
- 并查集的简单表示
- 并查集的合并
- 并查集的代码实现
- 并查集小练习1
- 并查集小练习2
- 并查集的压缩问题

一、并查集是什么

并查集是一个森林
在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-findset)。

0	1	2	3	4	5	6	7	8	9
-1	-1	-1	-1	-1	-1	-1	-1	-1	-1

比如：某公司今年校招全国总共招生10人，西安招4人，成都招3人，武汉招3人，10个人来自不同的学校，起先互不相识，每个学生都是一个独立的小团体，现给这些学生进行编号：{0, 1, 2, 3,4, 5, 6, 7, 8, 9}; 给以下数组用来存储该小集体，数组中的数字代表：该小集体中具有成员的个数。

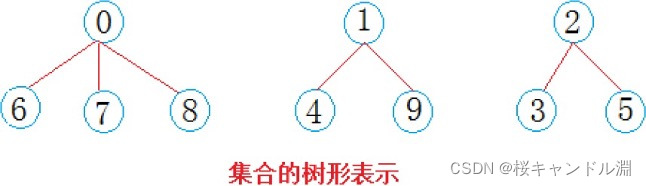
并查集的树的表示

所以说并查集就是在一堆的数据当中分出不同的集合。
当两个集合有交集的时候，这两个集合可能会被合并
所以称为并查集

如何让建立编号和人，人和编号的映射关系

#include <vector>
#include <map>
template<class T>
class UnionFindSet
{
public:
    UnionFindSet(const T*a,size_t n){
        for(size_t i=0;i<n;++i)
        {
            _a.push_back(a[i]);
            _indexMap[a[i]]=i;
        }
    }
private:
    vector<T> _a;//通过编号找人
    map<T,int> _indexMap;//通过人找编号
};

那么我们又如何表示人与人之间的关系呢？

1、像堆类似，用数组表示多棵树，用下表表示关系
2、双亲表示法

并查集的简单表示

最开始我们这里的每一个标号下面存的都是-1，表示每一个个体都是一个集合，这就是我们的最初始状态，表示十颗树，十个集合。

0	1	2	3	4	5	6	7	8	9
-1	-1	-1	-1	-1	-1	-1	-1	-1	-1

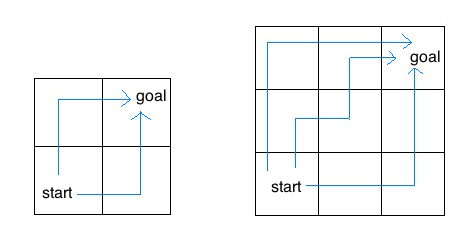
然后根据我们上面的图，我们知道我们的0,6,7,8号组成了我们的第一个小团体。
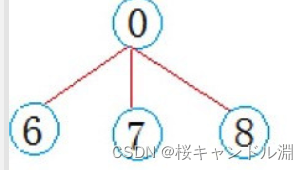
在这里插入图片描述

然后我们选择我们的0号作为我们第一个小团体的根节点，我们就将我们的1号存储的内容加上我们6号存储的内容。
然后我们将6号存储的内容变成1的索引，也就是变成我们下面的样子

0	1	2	3	4	5	6	7	8	9
-2	-1	-1	-1	-1	-1	0	-1	-1	-1

然后0再和7合并，变成我们下面的样子

0	1	2	3	4	5	6	7	8	9
-3	-1	-1	-1	-1	-1	0	0	-1	-1

然后0再和8合并，变成我们下面的样子

0	1	2	3	4	5	6	7	8	9
-4	-1	-1	-1	-1	-1	0	0	0	-1

特点

1.一个位置的值是负数，那它就是树的根，这个负数的绝对值就是这棵树的数据个数
2.如果一个位置的值是正数，那他存储的就是双亲的下标。

并查集的合并

所以按照我们上面的算法存储完毕之后，我们的并查集应该是如下的形状

0	1	2	3	4	5	6	7	8	9
-4	-3	-3	2	1	2	0	0	0	1

在公司工作一段时间后，西安小分队中8号同学与成都小分队1号同学奇迹般的走到了一起，两个小圈子的学生相互介绍，最后成为了一个小圈子：
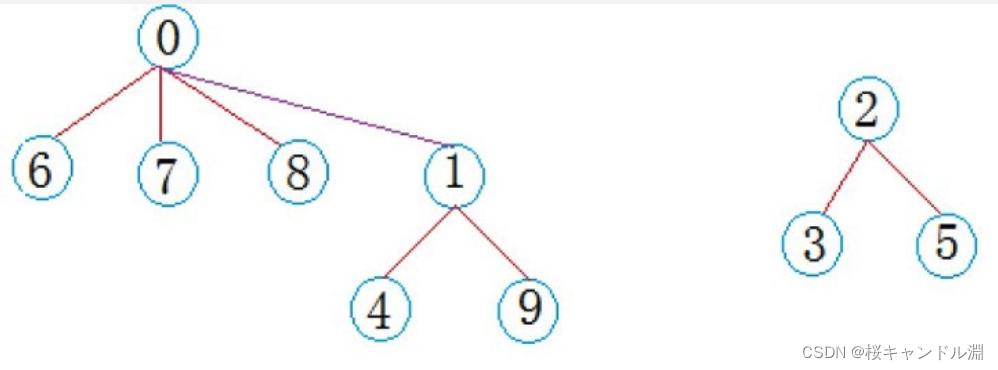
在这里插入图片描述

这时，我们就需要将1和8合并起来，但是8并不是父节点，所以我们查找8的父节点，我们发现是0号节点，所以我们将将1 中存储大的内容变成0，也就是其父节点是0号节点，然后我们的0号节点减去原本1号节点UN出的-3，也就是变成了-7

0	1	2	3	4	5	6	7	8	9
-7	0	-3	2	1	2	0	0	0	1

并查集的代码实现

#include <vector>
#include <map>
template<class T>
class UnionFindSet
{
public:
    UnionFindSet(size_t n)
        :_ufs(n,-1)
    {}

    void Unnion(int x1,int x2)
    {
        int root1= FindRoot(x1);
        int root2= FindRoot(x2);
        //如果本身`就是在一个集合当中，就没有必要合并了
        if(root1==root2)
            return;
        if(root1>root2)
            //将并查集中更大的那一个变成root1
            swap(root1,root2);
        //将我们的root2的集合合并到我们的root当中
        _ufs[root1]+=_ufs[root2];
        _ufs[root2]=root1;
    }
    int FindRoot(int x)
    {
        int parent=x;
        //如果不是负数，我就不是根
        while(_ufs[parent]>=0)
        {
            //不断查找父亲结点
            parent=_ufs[parent];
        }
        return parent;
    }
    //在不在同一个集合当中
    bool InSet(int x1,int x2)
    {
        //相等就是在一个集合，不相等就不再同一个集合
        return FindRoot(x1)== FindRoot(、x2);
    }
    size_t SetSize()
    {
        size_t size=0;
        for(size_t i=0;i<_ufs.size();++i)
        {
            if(_ufs[i]<0)
            {
                ++size;
            }
        }
        return size;
    }
private:
    vector<T> _ufs;//通过编号找人
};

并查集小练习1

LeetCode省份数量

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中省份的数量。

示例 1：
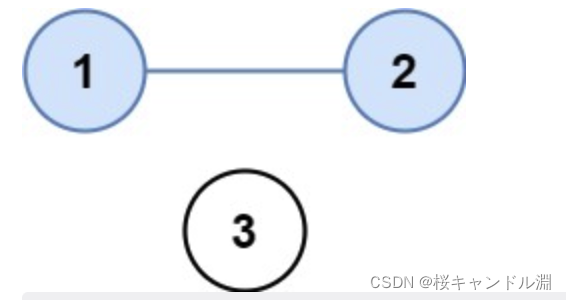
在这里插入图片描述

输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2
示例 2：
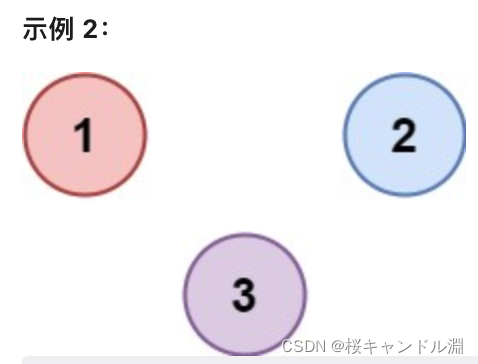
在这里插入图片描述

输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

提示：

1 <= n <= 200
n == isConnected.length
n == isConnected[i].length
isConnected[i][j] 为 1 或 0
isConnected[i][i] == 1
isConnected[i][j] == isConnected[j][i]

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/bLyHh0
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

class UnionFindSet
{
public:
    UnionFindSet(size_t n)
        :_ufs(n,-1)
    {}

    void Unnion(int x1,int x2)
    {
        int root1= FindRoot(x1);
        int root2= FindRoot(x2);
        //如果本身`就是在一个集合当中，就没有必要合并了
        if(root1==root2)
            return;
        if(root1>root2)
            //将并查集中更大的那一个变成root1
            swap(root1,root2);
        //将我们的root2的集合合并到我们的root当中
        _ufs[root1]+=_ufs[root2];
        _ufs[root2]=root1;
    }
    int FindRoot(int x)
    {
        int parent=x;
        //如果不是负数，我就不是根
        while(_ufs[parent]>=0)
        {
            //不断查找父亲结点
            parent=_ufs[parent];
        }
        return parent;
    }
    //在不在同一个集合当中
    bool InSet(int x1,int x2)
    {
        //相等就是在一个集合，不相等就不再同一个集合
        return FindRoot(x1)== FindRoot(x2);
    }
    size_t SetSize()
    {
        size_t size=0;
        for(size_t i=0;i<_ufs.size();++i)
        {
            if(_ufs[i]<0)
            {
                ++size;
            }
        }
        return size;
    }
private:
    vector<int> _ufs;//通过编号找人
};

class Solution {
public:
    int findCircleNum(vector<vector<int>>& isConnected) {
        UnionFindSet ufs(isConnected.size());

        for(size_t i=0;i<isConnected.size();++i)
        {
            for(size_t j=0;j<isConnected[i].size();++j)
            {
                //如果i和j是相连的话
                if(isConnected[i][j]==1)
                {
                    ufs.Unnion(i,j);
                }
            }
        }
        return ufs.SetSize();
    }
};

在这里插入图片描述

或者采用我们下面的更加简洁的版本

class Solution {
public:
    int findCircleNum(vector<vector<int>>& isConnected) {
        vector<int> ufs(isConnected.size(),-1);

        auto findRoot=[&ufs](int x){
            while(ufs[x]>=0)
            {
                x=ufs[x];
            }
            return x;
        };
        for(size_t i=0;i<isConnected.size();++i)
        {
            for(size_t j=0;j<isConnected[i].size();++j)
            {
                //如果i和j是相连的话
                if(isConnected[i][j]==1)
                {
                    //合并集合
                    int root1=findRoot(i);
                    int root2=findRoot(j);
                    if(root1!=root2)
                    {
                        ufs[root1]+=ufs[root2];
                        ufs[root2]=root1;
                    }
                }
            }
        }
        int n=0;
        for(auto e:ufs)
        {
            if(e<0)
            {
                ++n;
            }
        }
        return n;
    }
};

并查集小练习2

LeetCode等式方程的可满足性

给定一个由表示变量之间关系的字符串方程组成的数组，每个字符串方程 equations[i] 的长度为 4，并采用两种不同的形式之一：“a==b” 或 “a!=b”。在这里，a 和 b 是小写字母（不一定不同），表示单字母变量名。

只有当可以将整数分配给变量名，以便满足所有给定的方程时才返回 true，否则返回 false。

示例 1：

输入：[“a==b”,“b!=a”]
输出：false
解释：如果我们指定，a = 1 且 b = 1，那么可以满足第一个方程，但无法满足第二个方程。没有办法分配变量同时满足这两个方程。
示例 2：

输入：[“ba","ab”]
输出：true
解释：我们可以指定 a = 1 且 b = 1 以满足满足这两个方程。
示例 3：

输入：[“ab","bc”,“a==c”]
输出：true
示例 4：

输入：[“ab",“b!=c”,"ca”]
输出：false
示例 5：

输入：[“cc","bd”,“x!=z”]
输出：true

提示：

1 <= equations.length <= 500
equations[i].length == 4
equations[i][0] 和 equations[i][3] 是小写字母
equations[i][1] 要么是 ‘=’，要么是 ‘!’
equations[i][2] 是 ‘=’

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/satisfiability-of-equality-equations
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

class Solution {
public:
    bool equationsPossible(vector<string>& equations) {
        vector<int> ufs(26,-1);

        auto findRoot=[&ufs](int x){
            while(ufs[x]>=0)
            {
                x=ufs[x];
            }
            return x;
        };
        //第一遍，先把相等的值加到一个集合中
        for(auto& str :equations)
        {
            if(str[1]=='=')
            {
                int root1=findRoot(str[0]-'a');
                int root2=findRoot(str[3]-'a');
                if(root1!=root2)
                {
                    ufs[root1]+=ufs[root2];
                    ufs[root2]=root1;
                }
            }
        }

        //第二遍，部不相等的在不在一个集合，在的话就是相悖了，就返回false
        for(auto& str :equations)
        {
            if(str[1]=='!')
            {
                int root1=findRoot(str[0]-'a');
                int root2=findRoot(str[3]-'a');
                if(root1==root2)
                {
                    return false;
                }
            }
        }
        return true;
    }
};

在这里插入图片描述

并查集的压缩问题

当我们在处理数据量非常大的情况的时候，我们的可能需要压缩我们的路径
比方说我们下面的这种情况
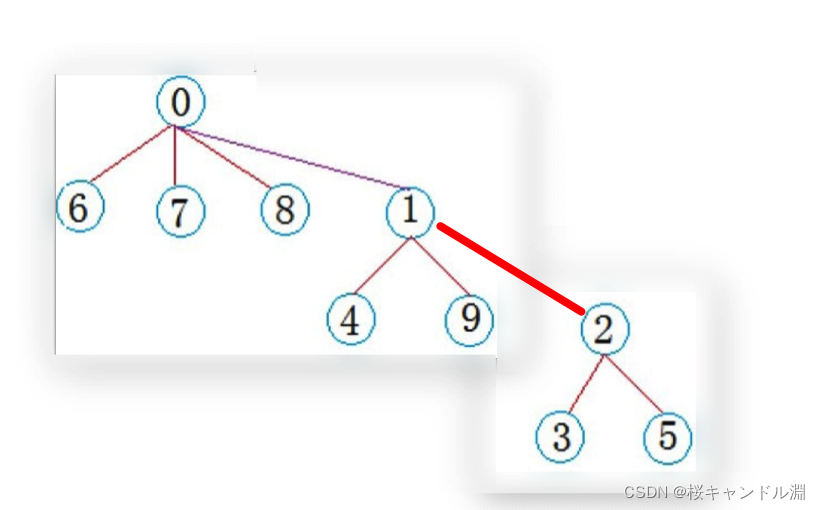
在这里插入图片描述
我们最好将我们的2的父节点更新成0，从而优化我们的路径。
什么时候优化我们的路径？
在查找我们的根结点的时候。
当你查找根节点的时候，发现查找的并不是一层根节点，我们就需要更新我们的根节点。
比方说我们上面2的父亲是1,1并不是根节点，1的父亲是0，我们就直接将我们2的路径变成0，这样之后再查找的时候，查找的速度就会变快。