更好的阅读体验

Lab 4: Recursion, Tree Recursion lab04.zip

What Would Python Do?

Q1: Squared Virahanka Fibonacci

Use Ok to test your knowledge with the following “What Would Python Display?” questions:
python3 ok -q squared-virfib-wwpd -u✂️

Hint: If you are stuck, try drawing out the recursive call tree. See 02/11’s Lecture (Tree Recursion) for more information.

>>> def virfib_sq(n):
...     print(n)
...     if n <= 1:
...         return n
...     return (virfib_sq(n - 1) + virfib_sq(n - 2)) ** 2
>>> r0 = virfib_sq(0)
? 0
-- OK! --

>>> r1 = virfib_sq(1)
? 1
-- OK! --

>>> r2 = virfib_sq(2)

(line 1)? 2
(line 2)? 1
(line 3)? 0
-- OK! --

>>> r3 = virfib_sq(3)

(line 1)? 3
(line 2)? 2
(line 3)? 1
(line 4)? 0
(line 5)? 1
-- OK! --

>>> r3
? 4
-- OK! --

>>> (r1 + r2) ** 2
? 4
-- OK! --

>>> r4 = virfib_sq(4)

(line 1)? 4
(line 2)? 3
(line 3)? 2
(line 4)? 1
(line 5)? 0
(line 6)? 1
(line 7)? 2
(line 8)? 1
(line 9)? 0
-- OK! --

>>> r4
? 25
-- OK! --

Parsons Problems

To work on these problems, open the Parsons editor:

python3 parsons

Q2: Line Stepper

Complete the function line_stepper, which returns the number of ways there are to go from start to 0 on the number line by taking exactly k steps along the number line. Note that at each step, you must travel either left or right; you may not stay in place!

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7cyFtIjp-1671289368934)(https://cs61a.org/lab/lab04/assets/line_stepper.png)]

For example, here is a visualization of all possible paths if we start at 3 on the number line with 5 steps. At every step, we move either one step to the left of right, and we ultimately end each path at 0.

def line_stepper(start, k):
    """
    Complete the function line_stepper, which returns the number of ways there are to go from
    start to 0 on the number line by taking exactly k steps along the number line.

    >>> line_stepper(1, 1)
    1
    >>> line_stepper(0, 2)
    2
    >>> line_stepper(-3, 3)
    1
    >>> line_stepper(3, 5)
    5
    """
    "*** YOUR CODE HERE ***"
    def line_stepper(start, k):
    if start == 0 and k == 0:
        return 1
    elif k == 0:
        return 0
    else:
        left = line_stepper(start - 1, k - 1)
        right = line_stepper(start + 1, k - 1)
        return left + right

Code Writing Questions

Q3: Summation

Write a recursive implementation of summation, which takes a positive integer n and a function term. It applies term to every number from 1 to n including n and returns the sum.

Important: Use recursion; the tests will fail if you use any loops (for, while).

def summation(n, term):
    """Return the sum of numbers 1 through n (including n) wíth term applied to each number.
    Implement using recursion!

    >>> summation(5, lambda x: x * x * x) # 1^3 + 2^3 + 3^3 + 4^3 + 5^3
    225
    >>> summation(9, lambda x: x + 1) # 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
    54
    >>> summation(5, lambda x: 2**x) # 2^1 + 2^2 + 2^3 + 2^4 + 2^5
    62
    >>> # Do not use while/for loops!
    >>> from construct_check import check
    >>> # ban iteration
    >>> check(HW_SOURCE_FILE, 'summation',
    ...       ['While', 'For'])
    True
    """
    assert n >= 1
    "*** YOUR CODE HERE ***"
    if n == 1:
        return term(n)
    else:
        return term(n) + summation(n - 1, term)

Use Ok to test your code:

python3 ok -q summation✂️

Q4: Insect Combinatorics

Consider an insect in an M by N grid. The insect starts at the bottom left corner, (1, 1), and wants to end up at the top right corner, (M, N). The insect is only capable of moving right or up. Write a function paths that takes a grid length and width and returns the number of different paths the insect can take from the start to the goal. (There is a closed-form solution to this problem, but try to answer it procedurally using recursion.)

grid

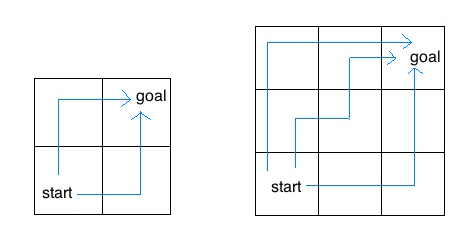
For example, the 2 by 2 grid has a total of two ways for the insect to move from the start to the goal. For the 3 by 3 grid, the insect has 6 diferent paths (only 3 are shown above).

Hint: What happens if we hit the top or rightmost edge?

def paths(m, n):
    """Return the number of paths from one corner of an
    M by N grid to the opposite corner.

    >>> paths(2, 2)
    2
    >>> paths(5, 7)
    210
    >>> paths(117, 1)
    1
    >>> paths(1, 157)
    1
    """
    "*** YOUR CODE HERE ***"
    if m == 1 and n == 1:
       return 1
    elif m == 0 or n == 0:
       return 0
    else:
        up = paths(m - 1, n)
        right = paths(m, n - 1)
        return up + right

Use Ok to test your code:

python3 ok -q paths✂️

Q5: Pascal’s Triangle

Pascal’s triangle gives the coefficients of a binomial expansion; if you expand the expression (a + b) ** n, all coefficients will be found on the nth row of the triangle, and the coefficient of the ith term will be at the ith column.

Here’s a part of the Pascal’s trangle:

Every number in Pascal’s triangle is defined as the sum of the item above it and the item above and to the left of it. Rows and columns are zero-indexed; that is, the first row is row 0 instead of 1 and the first column is column 0 instead of column 1. For example, the item at row 2, column 1 in Pascal’s triangle is 2.

Now, define the procedure pascal(row, column) which takes a row and a column, and finds the value of the item at that position in Pascal’s triangle. Note that Pascal’s triangle is only defined at certain areas; use 0 if the item does not exist. For the purposes of this question, you may also assume that row >= 0 and column >= 0.

def pascal(row, column):
    """Returns the value of the item in Pascal's Triangle
    whose position is specified by row and column.
    >>> pascal(0, 0)
    1
    >>> pascal(0, 5)	# Empty entry; outside of Pascal's Triangle
    0
    >>> pascal(3, 2)	# Row 3 (1 3 3 1), Column 2
    3
    >>> pascal(4, 2)     # Row 4 (1 4 6 4 1), Column 2
    6
    """
    "*** YOUR CODE HERE ***"
    if row == 0 and column == 0:
        return 1
    elif column == 0 or column == row:
        return 1
    elif column > row:
        return 0
    else:
        return pascal(row - 1, column - 1) + pascal(row - 1, column)