快速排序

快速排序关键在于确定一个中间值，使得小于这个中间值的数在左边，大于这个中间值的数在右边。那么中间值该如何确定呢？有以下几种做法

• 首元素，也就是arr[l]
• 尾元素，也就是arr[r]
• 中间元素，也就是arr[(l+r)>>1]这里是位运算，等价于arr[(l+r)/2^1]
• 中间的一个随机元素

void Qsort(int arr[],int l,int r){
	if(l>=r) return;
	int begin = l,end = r,x = arr[(l+r)>>1];
	//上面是位运算，表示(l+r)/2^1
	while(begin<=end){
		while(arr[begin]<x) begin++;
		while(arr[end]>x) end--;
		if(begin<=end) swap(&arr[begin++],&arr[end--]);
	}
	Qsort(arr,l,end);Qsort(arr,begin,r);
}
//除了和x的比较不带=，其他的都带

快速排序相关变体

题目如下：

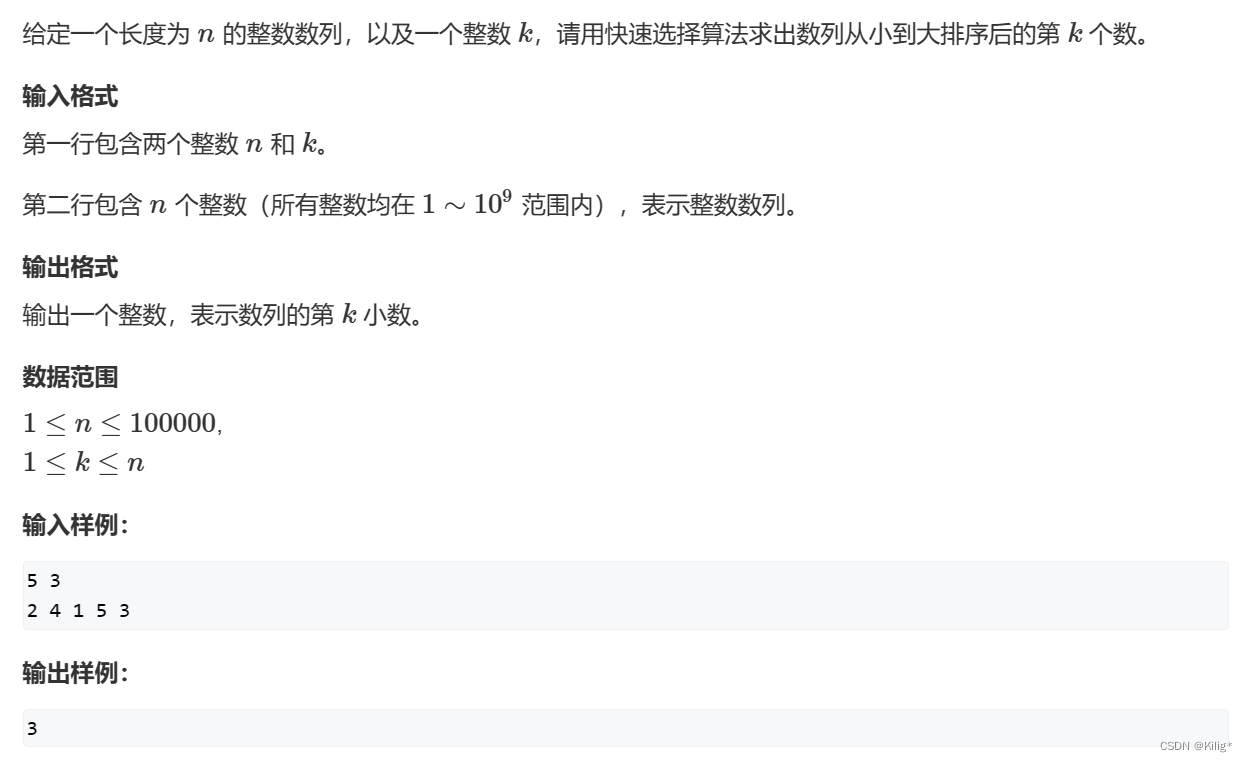
求第k大（小）的数，一种做法是堆排序把前k个数找出来就行，另一种就是利用快速排序的思想去做。现暂把中间的分界点称为pivot，左边的数都小于pivot，右边的数都大于pivot。那么假如左边有m个数，右边有n个数。求第k大的数。如果k<n，那么这个数肯定在右边，反之这个数肯定在左边。以此来缩小这个数所在的范围。

归并排序

归并排序的核心思想在于将两个有序的数组合并为一个全局有序的数组。

int tmp[100000];
void merge_sort(int arr[],int begin,int end){
    if(begin>=end) return;
    int mid = (begin+end)>>1;
    merge_sort(arr,begin,mid);
    merge_sort(arr,mid+1,end);
    int l_begin = begin,r_begin = mid+1,tmp_index = 0;
    while(l_begin<=mid && r_begin<=end)
    {
        if(arr[l_begin]<=arr[r_begin]) tmp[tmp_index++] = arr[l_begin++];
        else tmp[tmp_index++] = arr[r_begin++];
    }
    while(l_begin<=mid) tmp[tmp_index++] = arr[l_begin++];
    while(r_begin<=end) tmp[tmp_index++] = arr[r_begin++];
    int k = 0;
    while(begin<=end){
        arr[begin++] = tmp[k++];
    }
}