1.背景
这段内容主要是关于植物对干旱胁迫的反应,并介绍了生活在植物体内外以及根际的真菌和细菌的作用。然而,目前对这些真菌和细菌的稳定性了解甚少。作者通过调查微生物群落组成和微生物相关性的方法,对农业系统中真菌和细菌对干旱的抗性和恢复力进行了研究。研究结果显示,在微生物群落组成层面上,真菌比细菌更抗旱,但在重新灌溉缓解干旱压力后,真菌的恢复能力较低。然而,在所有相关性和共存网络方面,结果更加复杂。总体上,干旱会破坏细菌、真菌以及细菌与真菌之间显著正相关的微生物网络。令人惊讶的是,干旱加强了根际真菌与叶片细菌之间以及根际中丛枝菌根真菌相关性网络的结构。此外,研究还支持了应激梯度假说,因为干旱增加了正相关的相对频率。
2.假设
分析H1和H2假设在微生物群落组成层面上的测试结果。
- 假设1(H1):认为真菌群落比细菌群落更抗旱;
- 假设2(H2),认为真菌群落在重新灌水后的恢复能力比细菌群落更低。
3.实验
为了测试这两个假设,研究人员从同一片叶子、根系、根际和土壤样本中收集的高粱植株中获得了真菌和细菌的数据集,并进行了混合处理。这些植株分为两组,一组作为对照组进行正常灌溉,另一组在开花前经历了干旱处理,然后在开花后定期进行灌水。通过对这些数据集的分析,研究人员测试了H1和H2假设在微生物群落组成层面上的有效性。
4.专业知识
抗扰性(resistance)和复原力(resilience)
分析中的两个重要指标:抗扰性(resistance)和复原力(resilience)
- 抗扰性指的是社区在受到干扰后保持不变的程度
- 复原力则是社区在受到干扰后恢复到原始状态的速度。
真菌与细菌间的相互作用
微生物群落中的关联对生态系统稳定性的重要性。这些关联可以是正向或负向的,强弱不一,并涉及到细菌、真菌之间的相互作用。
有研究表明正向关联的比例与演替、施肥和栖息地等生态因素相关。
5.分析工具与特征
分析工具:Bray-Curtis dissimilarities
特征:根、根际、土壤和叶子等四个部分的细菌(红色和浅红色)和真菌(蓝色和浅蓝色)群落的差异。
6.R语言使用Bray-Curtis
1.安装包vegan,可以使用镜像源加速
代码
install.packages("vegan", repos="https://mirrors.tuna.tsinghua.edu.cn/CRAN/")
运行案例:
2.导入包vegan
代码
library(vegan)
运行案例
3.创建一个示例数据集
代码
data <- data.frame(
Sample1 = c(5,0,0,0),
Sample2 = c(0,10,0,0),
Sample3 = c(0,0,15,0),
Sample4 = c(0,0,0,20)
)
运行案例
3.计算Bray-Curtis距离
代码
bray_curtis_distance <- vegdist(data,method="bray")
运行案例
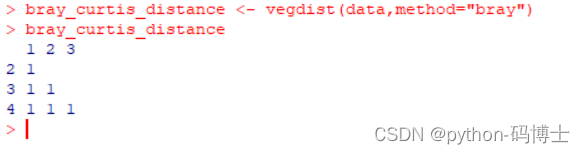
4.打印距离矩阵
代码
print(bray_curtis_distance)
运行案例

7.Bray-Curtis距离介绍
Bray-Curtis距离是以该统计指标的提出者J. Roger Bray和John T. Curtis的名字命名的,主要基于OTUs的计数统计,比较两个群落微生物的组成差异。与unifrac距离,包含的信息完全不一样;相比于jaccard距离,Bray-Curtis则包含了OTUs丰度信息。
bray-curtis距离
其中,S_(A,i)和S_(B,i)表示第i个OTU分别在A群落和B群落中的计数。min表示取两者最小值。
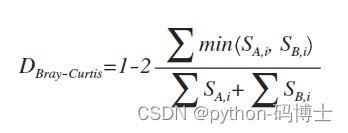
举例说明:
群落A和群落B的OTU统计如下表,
| community | OTU1 | OTU2 | OTU3 | OTU4 | OTU5 |
|---|---|---|---|---|---|
| A | 10 | 8 | 4 | 1 | 1 |
| B | 7 | 3 | 8 | 4 | 0 |
min(S_(A,i),S_(B,i)) = 7+3+4+1+0 = 15
sum(S_(A,i)) = 10+8+4+1+1 = 24
sum(S_(B,i)) = 7+3+4+8+4+0 = 22
D = 1 - 2*15/(24+22) = 0.3478
当然,D值越小越好,表示二者组成差异小。
8.问题与总结
- 从文章来理解:共存网络分析主要关注微生物个群在扰动下的共振变化,即仅关注显著的正相关关系。
- 需要加快理解数据的意义以及现有的分析手段
内容引自:Co-occurrence networks reveal more complexity than community composition in resistance and resilience of microbial communities