现象：
基础算法-递推算法-学习

方法：

这就是一种递推的算法思想。递推思想的核心就是从已知条件出发，逐步推算出问题的解

最常见案例：

一：正向递推案例：

弹力球回弹问题：
* 弹力球从100米高度自由落下，
* 每次落地后反跳回原高度的一半，并再落下
* 求它在第10次落地时，共经过多少米？第10次反弹多高？

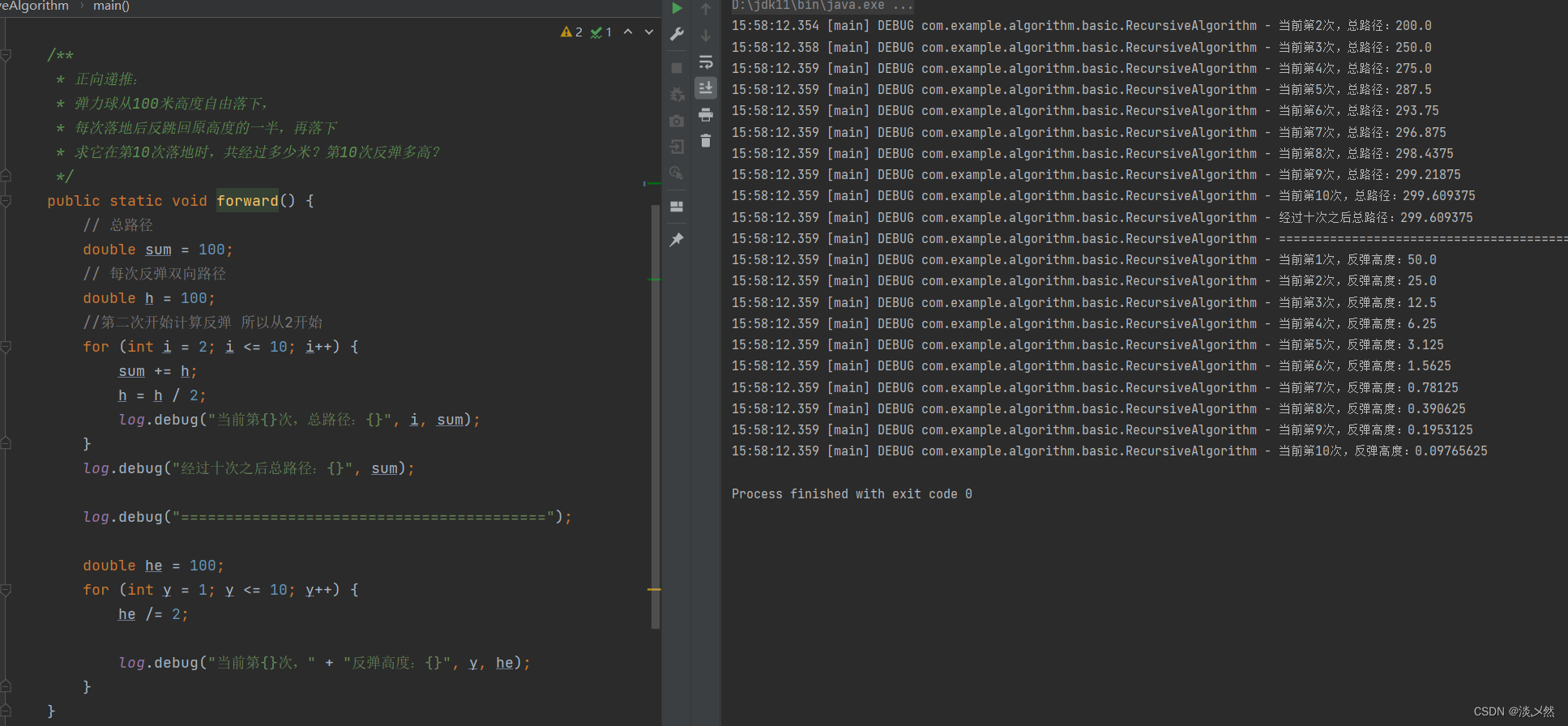
代码方法：

    public static void forward() {
        // 总路径
        double sum = 100;
        // 每次反弹双向路径
        double h = 100;
        //第二次开始计算反弹 所以从2开始
        for (int i = 2; i <= 10; i++) {
            sum += h;
            h = h / 2;
            log.debug("当前第{}次，总路径：{}", i, sum);
        }
        log.debug("经过十次之后总路径：{}", sum);

        log.debug("=========================================");

        double he = 100;
        for (int y = 1; y <= 10; y++) {
            he /= 2;

            log.debug("当前第{}次，" + "反弹高度：{}", y, he);
        }
    }

二：逆向递推案例：
小明吃饼干问题：
小明有一盒饼干
* 每天早上都吃一半，在分2块给同学
* 到第10天早上想再吃时，只剩下一块饼干了。求小明的一盒饼干有多少块？

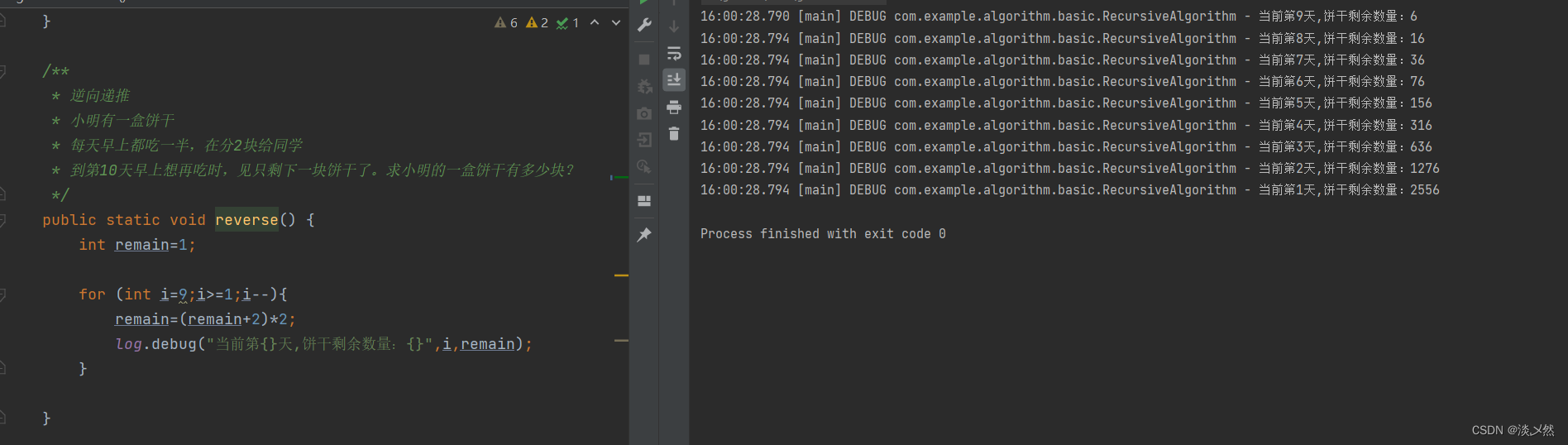
代码方法：

    public static void reverse() {
        int remain=1;

        for (int i=9;i>=1;i--){
            remain=(remain+2)*2;
            log.debug("当前第{}天,饼干剩余数量：{}",i,remain);
        }
    }

三：函数案例

斐波那契数列 \ 黄金分割数列
由意大利数学家列昂纳多・斐波那契（Leonardo Fibonacci）提出：
* 斐波那契数列指的是这样的一个数列：1、1、2、3、5、8、13、21、34、……，
* 这个数列从第 3 项开始，每一项都等于前面两项之和。在数学上斐波那契数列可以被递推的方法定义如下：
* F(1)=1，F(2)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 3，n ∈ N*）

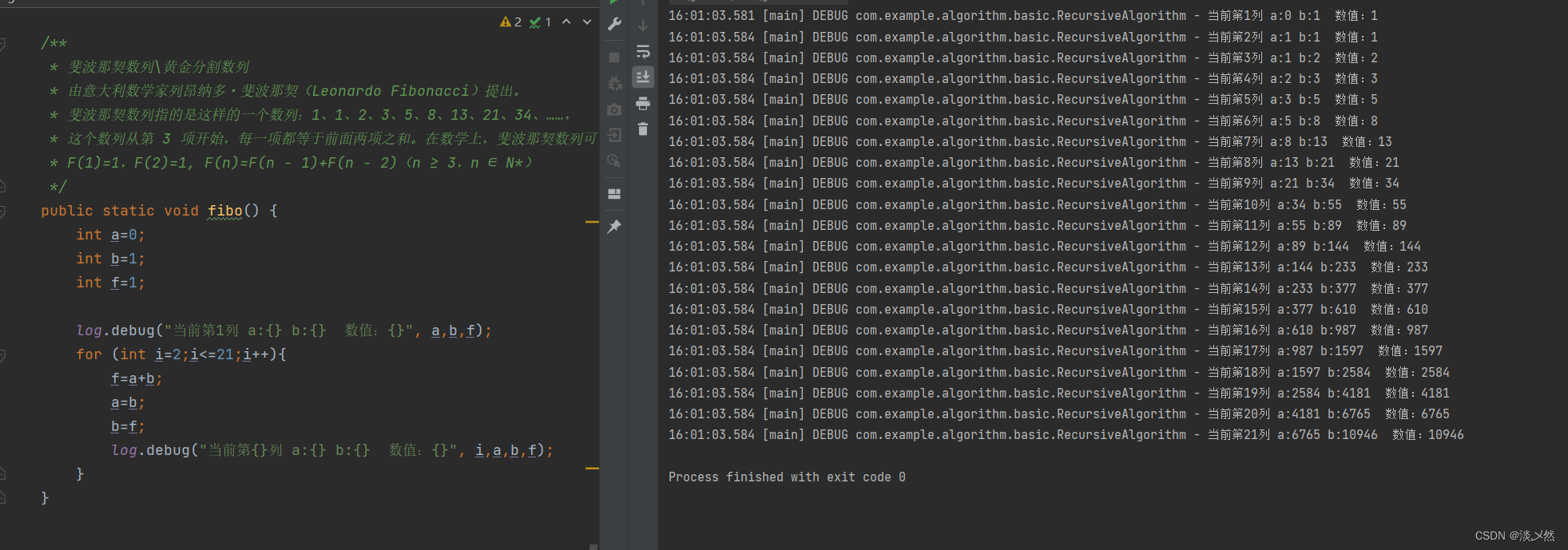
代码方法：

    public static void fibo() {
        int a=0;
        int b=1;
        int f=1;

        log.debug("当前第1列 a:{} b:{}  数值：{}", a,b,f);
        for (int i=2;i<=21;i++){
            f=a+b;
            a=b;
            b=f;
            log.debug("当前第{}列 a:{} b:{}  数值：{}", i,a,b,f);
        }
    }