🔆 文章首发于我的个人博客:欢迎大佬们来逛逛
数学建模:Logistic回归预测
Logistic回归预测
logistic方程的定义:
x t = 1 c + a e b t x_{t}=\frac{1}{c+ae^{bt}}\quad xt=c+aebt1
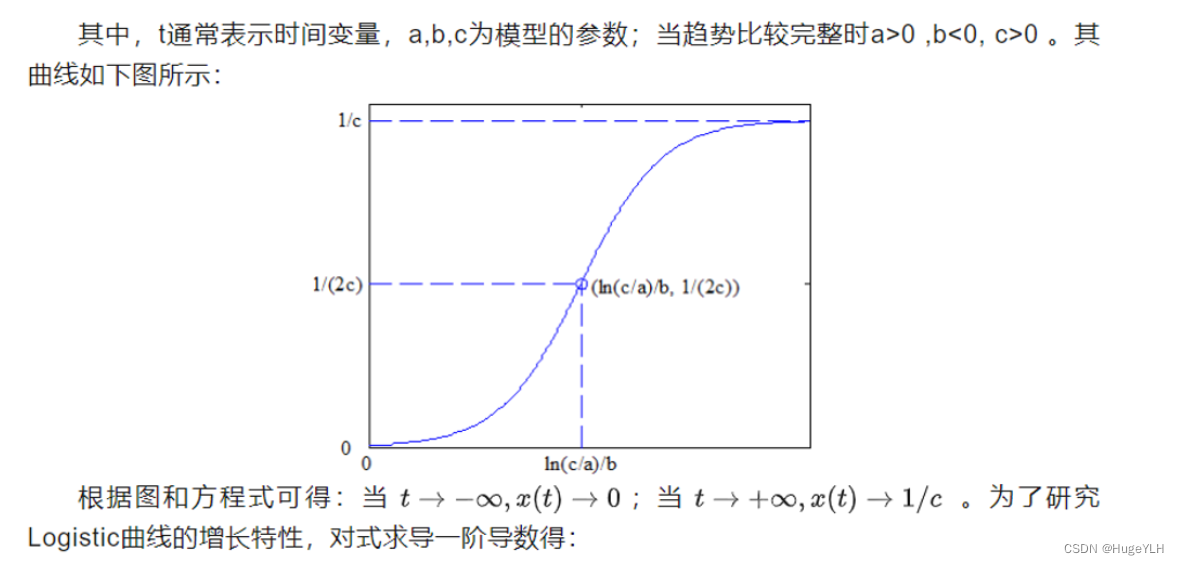
d x d t = − a b e b t ( c + a e b t ) 2 > 0 \frac{dx}{dt}=\frac{-abe^{bt}}{\left(c+ae^{bt}\right)^2}>0 dtdx=(c+aebt)2−abebt>0
算法流程
-
建立logistic方程
-
求解 其三个未知系数:
a,b,c -
Yule算法求解:构建如下的 线性方程 Z Z Z
x t + 1 − x t x t + 1 = 1 − x t x t + 1 = 1 − c + a e b ( t + 1 ) c + a e b t = ( a e b t + c − c ) ( 1 − e b ) ( c + a e b t ) = ( 1 − e b ) − c ( 1 − e b ) x t \begin{aligned}\frac{x_{t+1}-x_{t}}{x_{t+1}}=1-\frac{x_{t}}{x_{t+1}} \\&=1-\frac{c+ae^{b(t+1)}}{c+ae^{bt}} \\&=\frac{\left(ae^{bt}+c-c\right)\left(1-e^b\right)}{\left(c+ae^{bt}\right)} \\&=\left(1-e^b\right)-c\left(1-e^b\right)x_t\quad\end{aligned} xt+1xt+1−xt=1−xt+1xt=1−c+aebtc+aeb(t+1)=(c+aebt)(aebt+c−c)(1−eb)=(1−eb)−c(1−eb)xt
-
对此方程进行最小二乘法(OLS),得到方程的估计值,然后进而得到 a,b,c的值:
γ = 1 − e b 以及 β = − c ( 1 − e b ) , \gamma=1-e^b\text{ 以及 }\beta=-c\big(1-e^b\big), γ=1−eb 以及 β=−c(1−eb),
a ^ = e x p { 1 n [ ∑ t = 1 n l n ( 1 x t − c ^ − n ( n + 1 ) 2 b ^ ) ] } 5 ) \hat a=exp\bigg\{\frac{1}{n}\bigg[\sum_{t=1}^nln(\frac{1}{x_t}-\hat c-\frac{n(n+1)}{2}\hat b)\bigg]\bigg\}5) a^=exp{n1[t=1∑nln(xt1−c^−2n(n+1)b^)]}5)
- 然后需要预测自变量值 x x x 直接带入即可。
代码实现
function [a,b,c] = mfunc_Logistic(X)
% logistic 回归预测
% params:
% X: 输入向量
% returns:
% a,b,c: 分别为logistic的未知参数
n=length(X)-1;
% 得到线性方程: Z
for t=1:n
Z(t)=(X(t+1)-X(t))/X(t+1);
end
% 前面插一列全1向量
X1=[ones(n,1) X(1:n)']; % (46,2)
% 对线性方程 Z 进行最小二乘法OLS
% B:回归系数
% bint:回归系数的置信区间
% r:残差
% rint:残差的置信区间
% stats:包含四个统计量:R^2, F, 概率p, 估计误差方差
Y=Z';
[B,Bint,r,rint,stats]=regress(Y,X1);%最小二乘(OLS)
gamma=B(1,1);
beta=B(2,1);
%% 带入公式 计算logistic方程的 abc
b=log(1-gamma);
c=beta/(exp(b)-1);
a=exp((sum(log(1./X(1:n)-c))-n*(n+1)*b/2)/n);
end











![【01背包理论】01背包问题dp[i][j](二维数组) <动态规划板子>](https://img-blog.csdnimg.cn/ba1dcb9139914d10b6a79e57c69f2814.png)