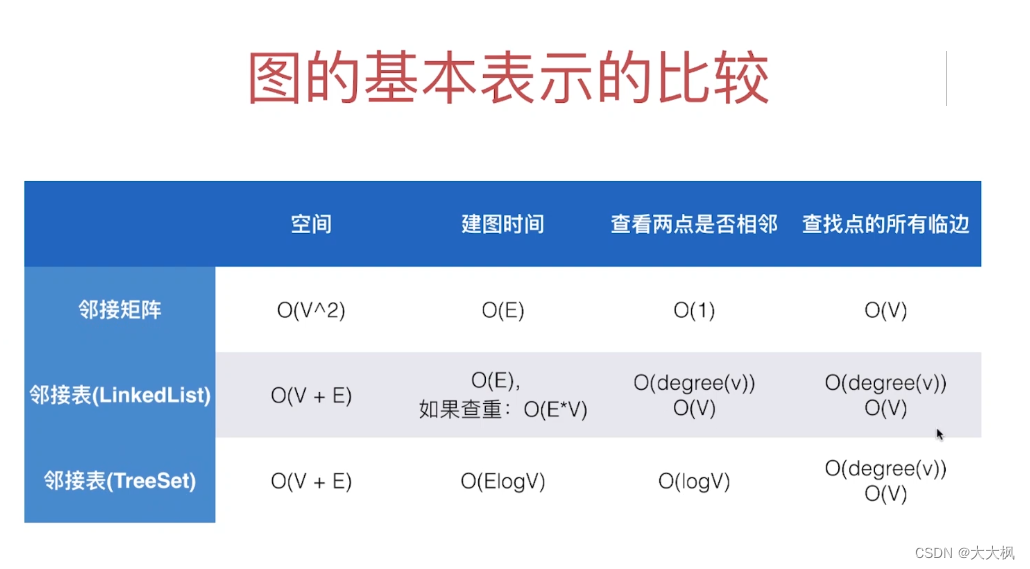
上篇博客介绍了图的概念与图的存储(邻接矩阵、邻接表): 接下来就是介绍图的遍历。
图的遍历
给定一个图G和其中任意一个顶点v0,从v0出发,沿着途中各边访问图中的所有顶点,且每个顶点仅被遍历一次。"遍历"即对结点进行某种操作的意思。
广度优先遍历
遍历原理
比如现在要找东西,假设有三个抽屉,东西在那个抽屉不清楚,现在要将其找到,广度优先遍历的做法是:

1. 先将三个抽屉打开,在最外层找一遍。
2. 将每个抽屉中的红色的盒子打开,再找一遍。
3. 将红色盒子中绿色盒子打开,再找一遍
找完所有的盒子,注意:每个盒子只能找一次,不能重复找。

第一个顶点入队列,然后再入与A顶点连通的顶点,再出A顶点,入与A顶点连通的顶点——B、C、D,当B出队列时,再入队列与B顶点联通的顶点,即A、C、E,因为A顶点之前已经入过队列了,则出现一个问题:如何防止节点被重复遍历。
则我们实现广度优先遍历要使用一个队列和一个标记结构(vector)。
实现步骤
1. 将顶点放入队列中。
2. 取出队列头部数据,将其标记数组中标记为已访问。
3. 把与该顶点相连通的顶点再放入队列中,在临界矩阵中则是纵向遍历。
4. 直到队列为空
void BFS(const V& src) //src是遍历的起点
{
size_t srci = GetVertexIndex(src);
//队列中存放下标
queue<int> q;
q.push(srci);
//标记位图
size_t sz = _vertexs.size();
vector<bool> visited(sz, false);
//如果不为空,就入队列
while (!q.empty())
{
int front = q.front();
q.pop();
cout << front << ":" << _vertexs[front] << endl;
//标记该结点
visited[front] = true;
//将front的邻接顶点入队列
for (size_t i = 0; i < sz; i++)
{
if (_matrix[front][i] != INT_MAX)
{
//如果该顶点没有出现过
if (visited[i] == false)
{
q.push(i);
visited[i] = true;
}
}
}
}
}
测试代码:

该测试代码的逻辑连通图:

广度优先遍历的应用

这道题目的实际就是让你实现广度优先遍历时实现对层数的控制。
具体实现就是在我们出完一度好友后,能够获取到下一度好友的数量,这个数量其实就是当前队列中剩余的好友的数量。
void BFS_level(const V& src) //src是遍历的起点
{
size_t srci = GetVertexIndex(src);
//队列中存放下标
queue<int> q;
q.push(srci);
//标记位图
size_t sz = _vertexs.size();
vector<bool> visited(sz, false);
int levelsize = q.size();
//如果不为空,就入队列
while (!q.empty())
{
for (int l = 0; l < levelsize; l++)
{
int front = q.front();
q.pop();
cout << front << ":" << _vertexs[front] << " ";
//标记该结点
visited[front] = true;
//将front的邻接顶点入队列
for (size_t i = 0; i < sz; i++)
{
if (_matrix[front][i] != INT_MAX)
{
//如果该顶点没有出现过
if (visited[i] == false)
{
q.push(i);
visited[i] = true;
}
}
}
}
cout << endl;
levelsize = q.size();
}
}运行结果:

深度优先遍历
遍历原理
如果使用深度优先遍历,那在这三个抽屉中找东西的步骤则是这样的:

1. 先将第一个抽屉打开,在最外层找一遍
2. 将第一个抽屉中的红盒子打开,在红盒子中找一遍
3. 将红盒子中绿盒子打开,在绿盒子中找一边
4. 递归查找剩余的两个盒子
深度优先遍历:将一个抽屉一次性遍历完(包括该抽屉中包含的小盒子),再去递归遍历其他盒子。

实现步骤
1. 取到该顶点,然后调用_DFS函数
2. _DFS函数中打印该顶点,然后将其标记
3. 遍历与该顶点相连通的顶点,在临界矩阵中则是纵向遍历。
4. 如果与其连通的不是顶点有权值,并且未访问过,则调用_DFS.
//深度遍历
void DFS(const V& src)
{
cout << "DFS:" << endl;
size_t srci = GetVertexIndex(src);
vector<bool> visited(_vertexs.size(), false);
_DFS(srci, visited);
}
void _DFS(size_t srci, vector<bool>& visited)
{
cout << srci << ": " << _vertexs[srci] << endl;
//标记该点已访问
visited[srci] = true;
//找一个srci相邻并未访问的顶点,去深度遍历
for (size_t i = 0; i < _vertexs.size(); i++)
{
if (_matrix[srci][i] != MAX_W && visited[i] == false)
{
_DFS(i, visited);
}
}
}测试:

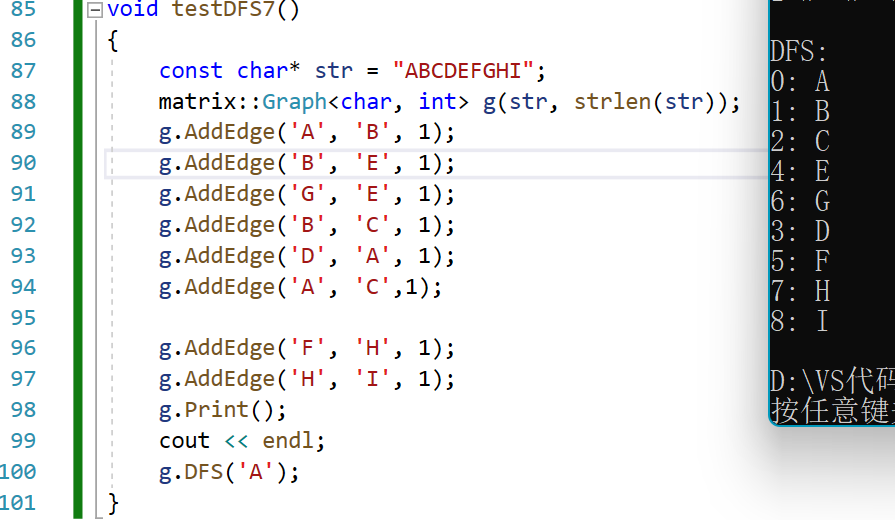
如果我们传入的是张三,则会遍历张三连通的节点,即李四,李四再遍历连通的节点,因为李四中张三是访问过的,则跳过张三,然后李四发现没有顶点与其连通,则返回。依次过程进行遍历。结果如上图。
非连通图的遍历
如果给定的图不是连通图,以某个点位起点就没有遍历完成。
以下图逻辑为例:


我们需要如果想将其全部遍历,则要配合使用我们的visited数组,遍历visited数组,将其中没有出现过的顶点作为参数再次调用DFS或BFS函数。
以下以DFS举例:
//深度遍历
void DFS(const V& src)
{
cout << "DFS:" << endl;
size_t srci = GetVertexIndex(src);
vector<bool> visited(_vertexs.size(), false);
_DFS(srci, visited);
//遍历未连通的顶点
for (size_t i = 0; i < visited.size(); i++)
{
if (visited[i] == false)
{
_DFS(i, visited);
}
}
}
void _DFS(size_t srci, vector<bool>& visited)
{
cout << srci << ": " << _vertexs[srci] << endl;
//标记该点已访问
visited[srci] = true;
//找一个srci相邻并未访问的顶点,去深度遍历
for (size_t i = 0; i < _vertexs.size(); i++)
{
if (_matrix[srci][i] != MAX_W && visited[i] == false)
{
_DFS(i, visited);
}
}
}遍历结果: