一、与字符串相关的动态规划
1.1题目
给定一个字符串str,给定一个字符串类型的数组arr,出现的字符都是小写英文arr每一个字符串,代表一张贴纸,你可以把单个字符剪开使用,目的是拼出str来返回需要至少多少张贴纸可以完成这个任务例子: str= “babac,arr = [ba”,“c”“abcd”]把每一个字符单独剪开,含至少需要两张贴纸"ba"和"abcd”,因为使用这两张贴纸,有2个a、2个b、1个c

先来看一下这个题目吧!
其实用自然智慧来解这道题时,我的脑子直接给出了比较简单的答案。
最少肯定是一张贴纸,但一张贴纸无论是ba c 还是abcd都满足不了;
然后试一试两张呢?ba+ba=baba还差一个c就可以了。
那1张不行,2 张可以,那最少就是两张了。
这种方法可以解决这个最简单的问题,同时也从这个方法中找到一个思路。
没有解决思路的时候,暴力递归/暴力枚举是最常使用的方法。
我用第一张贴纸字符串str2去拟合字符串str中的数据,得到了一个字符串str=str-str1。(这里的减法就是str1分别去掉str2中的字符。)
如果str不为空,还要继续用贴纸去拟合
然后用第二张贴纸字符串str去拟合str,得到了一个字符串str=str-str1。(这里的减法就是str1分别去掉str2中的字符。)
如果str不为空,还要继续用贴纸去拟合…
这不就是有重复调用的函数,那不就是递归了吗?而递归结束的条件就是字符串为空str=“”;
所以面对一个str,我们现在有一个贴纸数组arr,我们会有的第一步就是用一张贴纸去拟合str,但这张贴纸可以是arr数组中的每一张贴纸。
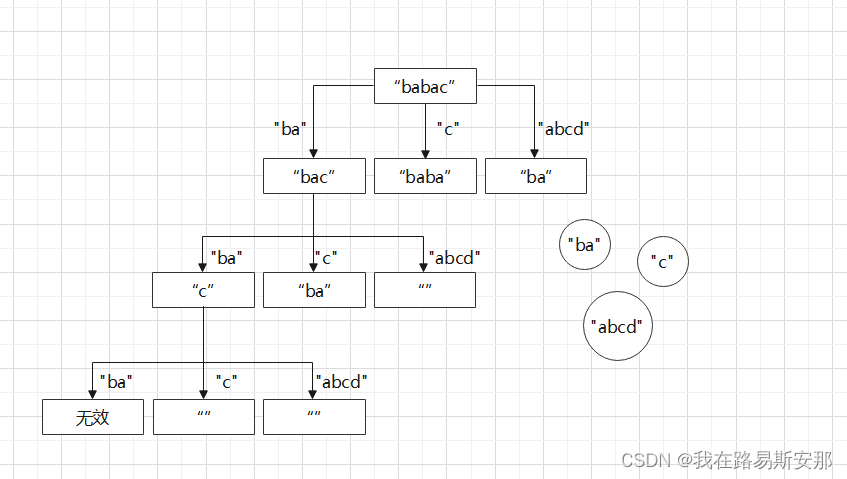
上图只做了最左边的分支的示例,每个结点都应该继续往下,这很明显就是一颗树状图哈哈。
从最后一层向上看,当str=“c”时,如果用“ba”去拟合,那你无论怎么努力都拟合不了,那就是无效的。如果我们把每一方框都看成一个节点,每个节点都有一个属性叫最小贴纸数min_num。
那么“”的min_num为0—向上一层经过一个边,那就用了一张贴纸,所以要加一。那么上一层的min_num=0+1;
则普遍的公式就是min_num(上层)=min_num(下层)+1;
1.2代码
有上面的思路走下来肯定是一个暴力递归,但是没关系,任何东西都是又暴力开始(和平大概也是,但希望不是~~~~(>_<)~~~~),那我们就来尝试写一下代码吧!
public class solu01 {
static String str = "baback";
static String[] sticker = {"ba", "ck", "abcd"};
public static void main(String[] args) {
ways1();
}
public static void ways1() {
int min_num = process1(str, sticker);
min_num=min_num==Integer.MAX_VALUE?0:min_num;
System.out.println(min_num);
}
public static int process1(String target, String[] sticker) {
if (target.length()==0) {
return 0;
}
int min_num = Integer.MAX_VALUE;
for (String s : sticker) {
String str = minus(target, s);
int min_num_next = Integer.MAX_VALUE;
;
if (!str.equals(target)) {
min_num_next = process1(str, sticker);
}
if (min_num_next != Integer.MAX_VALUE) {
min_num = Math.min(min_num, min_num_next + 1);
}
}
return min_num;
}
public static String minus(String str1, String str2) {
//可以看到这种贴纸类型的,可以将字符串剪开,其实无所谓顺序如何的,因此可以直接按照abc...这样的顺序来拍一下序
//有一种很巧妙的办法就是
int[] count = new int[26];//表示26个字母每一个出现的次数;
char[] chars1 = str1.toCharArray();//target
char[] chars2 = str2.toCharArray();
for (char c : chars1) {
count[c - 'a']++;
}
for (char c : chars2) {
count[c - 'a']--;
}
StringBuilder sb = new StringBuilder();
for (int i = 0; i < count.length; i++) {
if (count[i] != 0) {
for (int j = count[i]; j > 0; j--) {
sb.append((char) (i + 'a'));
}
}
}
return sb.toString();
}
}
1.3 代码优化
暴力递归之后该是什么呢?一般是用缓存去优化,但这里是一个与之前构建dp表不同的一个优化,他优化的点有两个一个是词频表的建立,一个是剪枝。
1)剪枝
先来说剪枝:
记不记得我们用一张贴纸先去拟合str,但我们这张贴纸就是按放在arr中的顺序都试一遍,没有什么策略。要说策略就是:按顺序都试一遍(很明显这是一句废话。)
但是有些你一眼看过去可能就觉得没必要啊。但这个一眼看过去转换成程序可以理解的描述,就是使用某种策略,直接排除某些选择,但又不影响结果。
比如说str=“babac”,那么我们就可以先去用含有‘b’的贴纸去拟合。
你说没‘b’的贴纸,可能有‘a’啊。
那我用‘b’拟合了,剩下的开头不就是‘a’吗,那还轮不到有‘b’没‘a’的贴纸吗?其实是不影响最后结果的。那么就没有必要把不含‘b’的贴纸放到我们所谓的*“第一张”*。
2)词频表
再来看看词频表,先说词频数组,词频数组是一个长度为26的数组,对于一个单词,统计每个字符输出的长度。比如“abc”的词频表如下图所示。
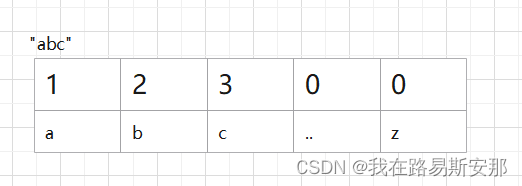
那如果我们建立贴纸数组的词频表数组{“ba”,“c”,“abcd”},其词频表:就是
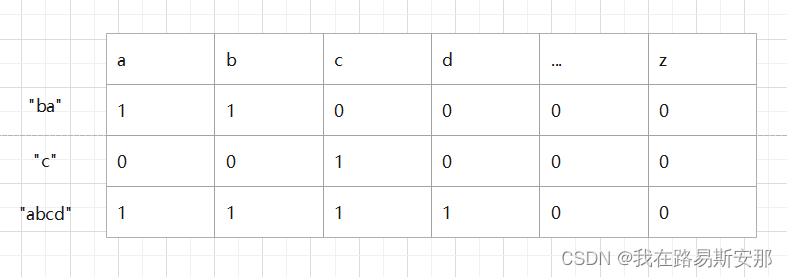
在第一部分的代码里面,我们每次都要建一次贴纸的词频表和target的词频数组,那么干脆就直接建好了开始用就行。
所以用“剪枝”和“词频表”优化之后的代码为:
public class solu02 {
static String str = "bababaq";
static String[] sticker = {"ba", "ck", "abcd"};
public static void main(String[] args) {
ways2();
}
public static void ways2() {
//建立词频表
int[][] sticker_count=new int[sticker.length][26];
for (int i=0;i<sticker.length;i++) {
char[] chars = sticker[i].toCharArray();
for (char aChar : chars) {
sticker_count[i][aChar-'a']++;
}
}
int min_num = process2(str, sticker_count);
min_num=min_num== Integer.MAX_VALUE?0:1;
System.out.println(min_num);
}
public static int process2(String s, int[][] sticker_count) {
if (s.length() == 0) {
return 0;
}
//0.设置要返回的变量
char[] target=s.toCharArray();
int min_num = Integer.MAX_VALUE;
//1.建立target词频数组
int[] target_count = new int[26];
for (char c : target) {
target_count[c - 'a']++;
}
//1.遍历贴纸词频表,找到所有分支种的最小值min_num
int N=sticker_count.length;
for (int i = 0; i < N; i++) {
int[] sticker = sticker_count[i];
//1.1如果这个贴纸包含target的第一个字符,我们可以选用这个贴纸作为第一张。
if (sticker[target[0] - 'a'] > 0) {
StringBuilder sb = new StringBuilder();
//1.2把目标字符串中中的贴纸减掉
for (int j = 0; j < 26; j++) {
if (target_count[j]>0) {
int num = target_count[j] - sticker[j];
for(int p=0;p<num;p++){
sb.append((char)(j+'a'));
}
}
}
//1.3恢复target
String rest = sb.toString();
min_num = Math.min(min_num, process2(rest, sticker_count));
}
}
//2.如果返回的是有效值,那么返回的是min_num+1;
return min_num+(min_num==Integer.MAX_VALUE?0:1);
}
}
1.4 优化进阶
这里我们可能要想到用缓存法来进行优化,但之前学习的缓存大多都是数组。这个里面一直变换的是谁?是target的字符串,这个字符串的状态如果都列出来占用空间会非常大,因此需要可以说没有严格的位置依赖。没有严格位置依赖但是依赖状态的,或者说状态无法穷举的,缓存就用hashmap来进行。
public class solu03 {
static String str = "bababakq";
static String[] sticker = {"ba", "ck", "abcd"};
public static void main(String[] args) {
ways3();
}
public static void ways3() {
//
HashMap<String,Integer> dp=new HashMap<>();
//建立词频表
int[][] sticker_count=new int[sticker.length][26];
for (int i=0;i<sticker.length;i++) {
char[] chars = sticker[i].toCharArray();
for (char aChar : chars) {
sticker_count[i][aChar-'a']++;
}
}
int min_num = process3(str, sticker_count,dp);
min_num=min_num== Integer.MAX_VALUE?0:min_num;
System.out.println(min_num);
}
public static int process3(String s, int[][] sticker_count, HashMap<String , Integer> dp) {
if(dp.containsKey(s)){
return dp.get(s);
}
if (s.length() == 0) {
return 0;
}
//0.设置要返回的变量
char[] target=s.toCharArray();
int min_num = Integer.MAX_VALUE;
//1.建立target词频数组
int[] target_count = new int[26];
for (char c : target) {
target_count[c - 'a']++;
}
//1.遍历贴纸词频表,找到所有分支种的最小值min_num
int N=sticker_count.length;
for (int i = 0; i < N; i++) {
int[] sticker = sticker_count[i];
//1.1如果这个贴纸包含target的第一个字符,我们可以选用这个贴纸作为第一张。
if (sticker[target[0] - 'a'] > 0) {
StringBuilder sb = new StringBuilder();
//1.2把目标字符串中中的贴纸减掉
for (int j = 0; j < 26; j++) {
if (target_count[j]>0) {
int num = target_count[j] - sticker[j];
for(int p=0;p<num;p++){
sb.append((char)(j+'a'));
}
}
}
//1.3恢复target
String rest = sb.toString();
min_num = Math.min(min_num, process3(rest, sticker_count,dp));
}
}
//2.如果返回的是有效值,那么返回的是min_num+1;
min_num=min_num+(min_num==Integer.MAX_VALUE?0:1);
dp.put(s,min_num);
return min_num;
}
}