最小二乘法是一种数学优化技术,用于查找最适合一组数据点的函数。 该方法主要用于线性回归分析,当然,也可用于非线性问题。
开始之前,我们先理解一下什么是回归。
回归:回归是一种监督学习算法,用于建模和分析两个或多个变量之间的关系。 具体来说,回归分析旨在了解自变量(输入特征)和因变量(输出或目标)之间的关系。 当您有数据点并想要使用一个或多个变量来预测或解释另一个变量时,通常会使用回归分析。
回归有很多中:
-
线性回归:因变量和自变量之间的关系被建模为线性方程
y = a x + b y=ax+b y=ax+b -
多元线性回归:允许有两个或多个自变量。
y = a 1 x 1 + a 2 x 2 + ⋯ + a n x n + b y=a 1x 1+a 2x 2+⋯+a nx n+b y=a1x1+a2x2+⋯+anxn+b -
多项式回归:因变量和自变量之间的关系被建模为多项式方程。
y = a 1 x 2 + a 2 x + b y=a 1x 2+a 2x+b y=a1x2+a2x+b
- 逻辑回归、岭回归、决策树回归、随机森林回归等等…
由于一些问题,这里我们只从简单的线性回归开始。 如果还有其他疑问,或者想了解更多内容,欢迎评论。
简单线性方程公式如下:
y = a x + b y=ax+b y=ax+b
其中:
- y 是因变量
- x 是自变量
- a 是斜率
- b 是截距
x 和 y 是我们已知的值。 当我们找到a和b的值时,我们可以将它们带入公式来解决线性回归问题。
要求斜率和截距的值,可以使用最小二乘法来计算。
最小二乘法求解a、b公式如下:
a = n ( ∑ x y ) − ( ∑ x ) ( ∑ y ) n ( ∑ x 2 ) − ( ∑ x ) 2 a = \frac{n(\sum xy) - (\sum x)(\sum y)}{n(\sum x^2) - (\sum x)^2} \ a=n(∑x2)−(∑x)2n(∑xy)−(∑x)(∑y)
b = ∑ y − a ∑ x n b = \frac{\sum y - a \sum x}{n} \ b=n∑y−a∑x
其中:
- ∑ x \sum x ∑x 是 x 值的总和
- ∑ y \sum y ∑y 是 y 值的总和
- ∑ x y \sum xy ∑xy 是 x 和 y 的乘积的总和
- ∑ x 2 \sum x^2 ∑x2 是 x 的平方的总和
- n n n 是样本数量
假设我们有一堆数据:
a = [[1, 2], [2, 4], [3, 3], [4, 6], [5, 6]]

让我们使用这些公式来手动计算 a 和 b 的值:
import numpy as np
a = np.array([[1, 2], [2, 4], [3, 3], [4, 6], [5, 6]])
x = a[:, 0]
y = a[:, 1]
n = len(x)
sum_x = np.sum(x)
sum_y = np.sum(y)
sum_x2 = np.sum(x ** 2)
sum_xy = np.sum(x * y)
slope = (n * sum_xy - sum_x * sum_y) / (n * sum_x2 - sum_x ** 2)
intercept = (sum_y - slope * sum_x) / n
slope, intercept
你可以复制自己尝试一下,或者依此作为参考按照自己的想法手写一个。
得出的值为(1.0, 1.2),所以使用最小二乘法,我们得到拟合直线的斜率 a=1.0 和截距 b=1.2。因此,这条最佳拟合直线的方程是 y = 1.0 x + 1.2 y=1.0x+1.2 y=1.0x+1.2。
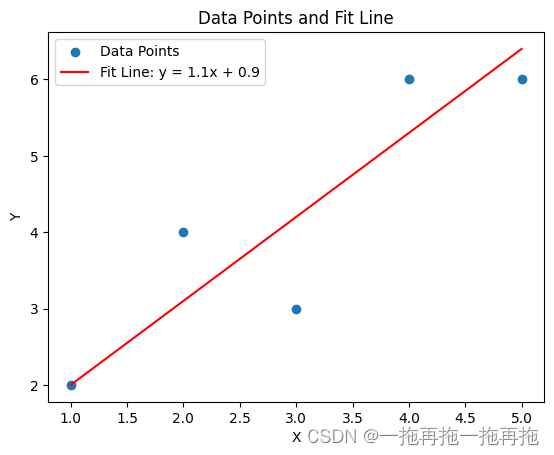
有了这个公式,就可以进行预测了,比如我有一个坐标x=10,根据x来预测y的值:
y=1.0*10+1.2 = 11.2
如果你已经准备好了或者想使用现有库,可以:
- 使用线性回归根据评分预测票房
此外,你也可以尝试搜索更多数据集,比如房价,汽车速度等,完成更多挑战。