Xgboost

XGBoost（eXtreme Gradient Boosting）是一种机器学习算法，是梯度提升决策树（Gradient Boosting Decision Trees）的一种优化实现。它是由陈天奇在2014年开发并推出的。XGBoost是一种强大而高效的算法，被广泛用于解决各种机器学习问题，包括分类、回归、排序、推荐和异常检测等。它结合了梯度提升算法的优点，通过并行处理和优化技术，达到了高性能和高准确性的平衡。

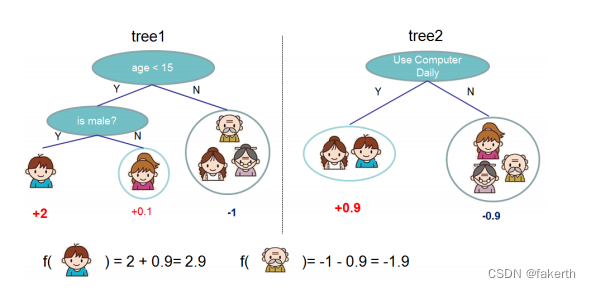
先来举个例子，我们要预测一家人对电子游戏的喜好程度，考虑到年轻和年老相比，年轻更可能喜欢电子游戏，以及男性和女性相比，男性更喜欢电子游戏，故先根据年龄大小区分小孩和大人，然后再通过性别区分开是男是女，逐一给各人在电子游戏喜好程度上打分，得到tree1。同时对电子游戏的喜好程序一定程度上可以从每天用电脑的时间分析，得到tree2。两棵树的结论累加起来便是最终的结论，所以小孩的预测分数就是两棵树中小孩所落到的结点的分数相加：2 + 0.9 = 2.9。爷爷的预测分数同理：-1 + （-0.9）= -1.9

目标函数

• 红色箭头所指向的L 即为损失函数（比如平方损失函数：l(yi,yi)=(yi−yi)²)
• 红色方框所框起来的是正则项（包括L1正则、L2正则）
• 红色圆圈所圈起来的为常数项
• 对于f(x)，XGBoost利用泰勒展开三项，做一个近似。f(x)表示的是其中一颗回归树。

Xgboost核心思想

1.不断地添加树，不断地进行特征分裂来生长一棵树，每次添加一个树，其实是学习一个新函数f_t(x)，去拟合上次预测的残差，新添加的f_t(x)使得我们的目标函数尽量最大地降低。

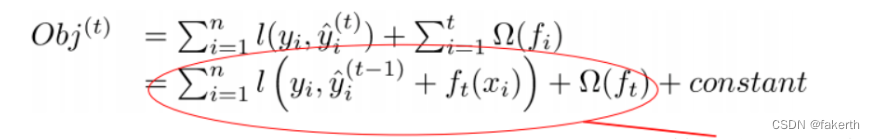
2.当我们训练完成得到k棵树，我们要预测一个样本的分数，其实就是根据这个样本的特征，在每棵树中会落到对应的一个叶子节点，每个叶子节点就对应一个分数。

3.最后只需要将每棵树对应的分数加起来就是该样本的预测值。

如何选择每一轮加入什么树呢？答案是非常直接的，选取一个 f 来使得我们的目标函数尽量最大地降低。这里 f 可以使用泰勒展开公式近似。

正则项

Xgboost的目标函数（损失函数+正则项表达）：

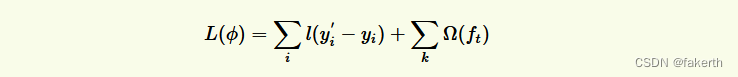
一般的目标函数都包含这两项，其中，误差/损失函数鼓励我们的模型尽量去拟合训练数据，使得最后的模型会有比较少的 bias。而正则化项则鼓励更加简单的模型。因为当模型简单之后，有限数据拟合出来结果的随机性比较小，不容易过拟合，使得最后模型的预测更加稳定。

如下图所示，xgboost对树的复杂度包含了两个部分：

• 一个是树里面叶子节点的个数T
• 一个是树上叶子节点的得分w的L2模平方（对w进行L2正则化，相当于针对每个叶结点的得分增加L2平滑，目的是为了避免过拟合）

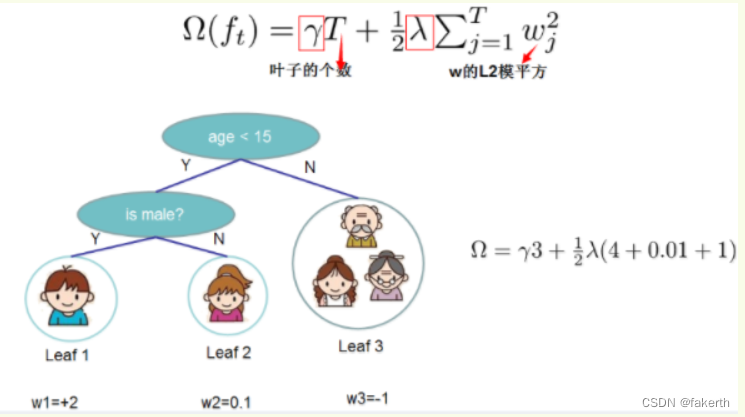
在这种新的定义下，我们可以把之前的目标函数进行如下变形：

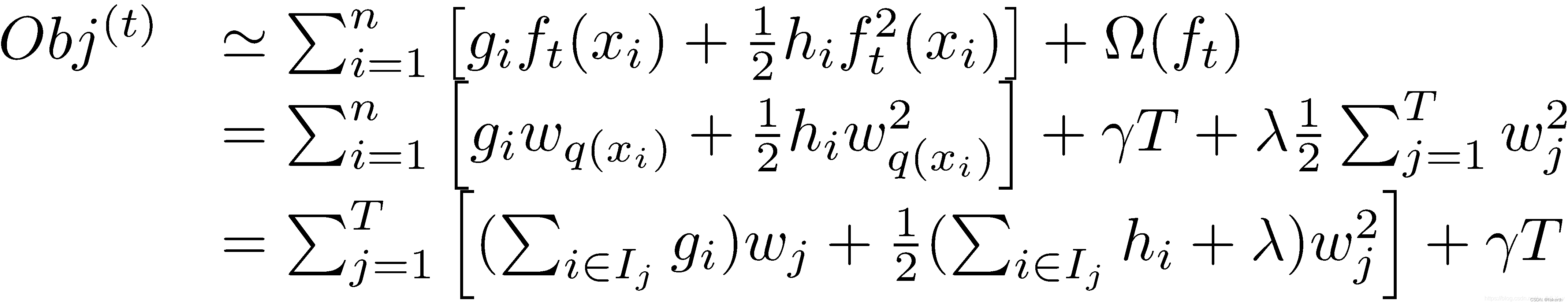
接着，我们可以定义：

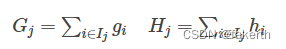
最终公式可以化简为：

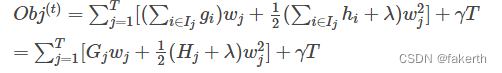
通过对w_j求导等于0，可以得到：

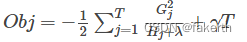
分裂节点

• （1）枚举所有不同树结构的贪心法

从树深度0开始，每一节点都遍历所有的特征，比如年龄、性别等等，然后对于某个特征，先按照该特征里的值进行排序，然后线性扫描该特征进而确定最好的分割点，最后对所有特征进行分割后，我们选择所谓的增益Gain最高的那个特征。

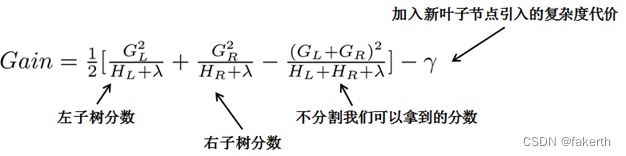
• （2）近似算法

主要针对数据太大，不能直接进行计算。

设置阈值，只有增益大于该阈值时才进行分裂。

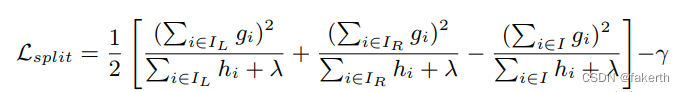
Xgboost模型参数

1.General Parameters (通用参数)

• booster[默认gbtree]，选择每次迭代的模型，有两种选择: gbtree:基于树模型；gblinear:线性模型。
• silent[默认为0]，当设置为1的时候，静默模式开启，不会输出任何信息。
• nthread [默认为最大可能的线程数]，这个参数用来进行多线程控制，应当输入系统的核数；若不设置，CPU会用全部的核。

2.Booster Parameters（模型参数)

• eta [默认值= 0.3]，类似于GBM中的学习率，通过缩小每一步的权重，使模型更加鲁棒，典型的最终使用值：0.01-0.2。
• min_child_weight [default = 1]，定义所需观察的最小权重总和。用于控制过度配合。较高的值会阻止模型学习关系，这种关系可能对为树选择的特定样本高度特定。太高的值会导致欠拟合，因此应使用CV进行调整。
• max_depth [default = 6]，树的最大深度，与GBM相同。用于控制过度拟合，因为更高的深度将允许模型学习非常特定于特定样本的关系。应该使用CV进行调整。典型值：3-10
• max_leaf_nodes，树中终端节点或叶子的最大数量。可以定义代替max_depth。由于创建了二叉树，因此深度n将产生最多2ⁿ个叶子。
• gamma [default = 0]，如果分裂能够使loss函数减小的值大于gamma，则这个节点才分裂。gamma设置了这个减小的最低阈值。如果gamma设置为0，表示只要使得loss函数减少，就分裂使算法保守。值可能会根据损耗函数而有所不同，因此应进行调整。
• max_delta_step [default = 0]，在最大增量步长中，我们允许每棵树的权重估计。如果该值设置为0，则表示没有约束。如果将其设置为正值，则可以帮助使更新步骤更加保守。通常不需要此参数，但是当类非常不平衡时，它可能有助于逻辑回归。
• Subsample[default = 1]，与GBM的子样本相同。表示观察的比例是每棵树的随机样本。较低的值使算法更加保守并防止过度拟合，但过小的值可能导致不合适。典型值：0.5-1。
• colsample_bytree [default = 1]，与GBM中的max_features类似。表示每个树的随机样本列的比例。典型值：0.5-1。
• colsample_bylevel [default = 1]，表示每个级别中每个拆分的列的子采样率。我不经常使用它，因为subsample和colsample_bytree会为你完成这项工作。但如果你有这种感觉，你可以进一步探索。
• lambda [default = 1]，关于权重的L2正则项（类似于岭回归），这用于处理XGBoost的正则化部分。虽然许多数据科学家不经常使用它，但应该探索减少过度拟合。
• alpha [默认= 0]，L1正则化项的权重（类似于Lasso回归），可以在非常高维度的情况下使用，以便算法在实现时运行得更快。
• scale_pos_weight [default = 1]，在高级别不平衡的情况下，应使用大于0的值，因为它有助于更​​快的收敛。
• n_estimators，对原始数据集进行有放回抽样生成的子数据集个数，即决策树的个数。若n_estimators太小容易欠拟合，太大不能显著的提升模型，所以n_estimators选择适中的数值。

3.Learning Task Parameters (学习任务参数)

• Objective [default = reg：linear]，这定义了要最小化的损失函数。最常用的值是：

  • binary:logistic， -logistic回归用于二进制分类，返回预测概率（不是类）
  • multi:softmax，使用softmax的多分类器，返回预测类（不是概率）
    • 您还需要设置一个额外的 num_class （类数）参数，用于定义唯一类的数量
  • multi:softprob，和multi:softmax参数一样，但返回属于每个类的每个数据点的预测概率。

• eval_metric [默认根据objective参数的取值]，用于验证数据的度量标准。回归的默认值为rmse，分类的误差为error。典型值为：

  • rmse - 均方根误差
  • mae - 平均绝对误差
  • logloss - 负对数似然
  • error - 二进制分类错误率（0.5阈值）
  • merror - 多类分类错误率
  • mlogloss - 多类logloss
  • auc： 曲线下面积
• 3. seed(默认为0)， 随机数的种子，设置它可以复现随机数据的结果，也可以用于调整参数。

Xgboost回归模型，通过features预测value

import os
import pandas as pd
import numpy as np
import sklearn
import xgboost as xgb
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
from tqdm import tqdm
from MyModel.utils.features import *
import warnings
warnings.filterwarnings("ignore")


def huber_approx_obj(y_pred, y_test):
    d = y_pred - y_test
    h = 5  # h is delta in the graphic
    scale = 1 + (d / h) ** 2
    scale_sqrt = np.sqrt(scale)
    grad = d / scale_sqrt
    hess = 1 / scale / scale_sqrt
    return grad, hess


def load_datasets():
    pd.set_option('display.max_columns', 1000)
    pd.set_option('display.width', 1000)
    pd.set_option('display.max_colwidth', 1000)

    df = pd.read_pickle('****.pickle')
    features = ["key1","key2","key3","key4","key5","key6","key7"]
    print(df.head(10))

    df_train, df_test = sklearn.model_selection.train_test_split(df, test_size=0.2)

    X_train, X_test = df_train[features], df_test[features]

    print(X_test)
    y_train, y_test = df_train["value"], df_test["value"]

    print(y_test)

    return X_train, X_test, y_train, y_test


def model_train(X_train, X_test, y_train, y_test):
    regressor = xgb.XGBRegressor(obj=huber_approx_obj, n_estimators=12, max_depth=64, colsample_bytree=0.8)
    print(len(X_train))
    regressor.fit(X_train, y_train, eval_metric=huber_approx_obj)
    y_pred_test = regressor.predict(X_test)

    print(y_test)
    print(y_pred_test)
    error = np.median(10 ** np.abs(y_test - y_pred_test))
    print(error)


def main():
    X_train, X_test, y_train, y_test = load_datasets()
    model_train(X_train, X_test, y_train, y_test)


if __name__ == "__main__":
    main()