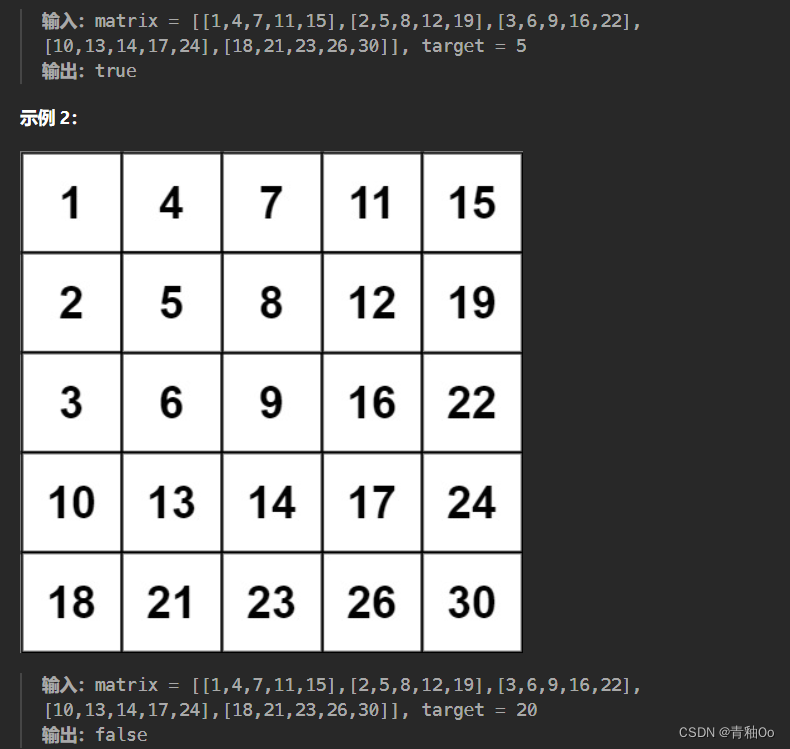
题目链接：二分图的最大匹配

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 510, M = 100010;

int n1, n2, m;
int h[N], e[M], ne[M], idx;

// 右边点所对应的左边的点
int match[N];
bool st[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

bool find(int x)
{
    for(int i = h[x]; i != -1; i = ne[i])
    {
        int j = e[i];
        if(!st[j])
        {
            st[j] = true;
            if(match[j] == 0 || find(match[j]))
            {
                match[j] = x;
                return true;
            }
        }
    }
    return false;
}

int main()
{
    cin >> n1 >> n2 >> m;
    memset(h, -1, sizeof h);
    while(m--)
    {
        int a, b;
        cin >> a >> b;
        add(a, b);
    }
    int res = 0;
    for(int i = 1; i <= n1; i ++)
    {
        memset(st, false, sizeof st);
        if(find(i)) res ++;
    }
    cout << res << endl;
    
    return 0;
}