前言:
我们学过不少优化类的算法了,大部分都是基于凸函数的性质给出的优化,比如Slope Trick,Wqs二分,又比如今天的斜率优化(不知道什么时候会有空把Slope Trick写掉)
正文:
我们考虑一类比较常见的dp方程: d p i = m i n / m a x j ( a i ∗ b j + c j + d i ) dp_i=min/max_{j}(a_i*b_j+c_j+d_i) dpi=min/maxj(ai∗bj+cj+di),其中 b j b_j bj是单调增的(事实上 b j b_j bj不单调增也可以用斜率优化处理,但是这里我们为了简化先考虑这样一种特殊情况)。同时,为了方便,接下来我们先以min为讨论对象,实际上max是同理的,读者可以自己对应手推一遍
一般的暴力递推,复杂度是 O ( N 2 ) O(N^2) O(N2)的。
我们考虑改变一下式子的形式: d p i = m i n j { a i ∗ b j + c j } + d i dp_i=min_{j}\{a_i*b_j+c_j\}+d_i dpi=minj{ai∗bj+cj}+di,此时对于固定的 i i i,外面的 d i d_i di是固定的,所以我们真正要考虑的其实是 a i ∗ b j + c j a_i*b_j+c_j ai∗bj+cj这样一个式子的最小值,它其实就是一个一次函数 k x + b kx+b kx+b的形式,其中 k = b j , b = c j k=b_j,b=c_j k=bj,b=cj。我们不妨记 f i , j = a i ∗ b j + c j f_{i,j}=a_i*b_j+c_j fi,j=ai∗bj+cj
凸包
我们不妨来看一下,如果两个点 x < y x<y x<y,对于某一个i满足 f ( i , y ) ≤ f ( i , x ) f(i,y)\leq f(i,x) f(i,y)≤f(i,x),也就是说 y y y是比 x x x更加优的一个决策点,它们之间会有什么关系
f ( i , y ) = a i ∗ b y + c y ≤ f ( i , x ) = a i ∗ b x + c x f(i,y)=a_i*b_y+c_y\leq f(i,x)=a_i*b_x+c_x f(i,y)=ai∗by+cy≤f(i,x)=ai∗bx+cx
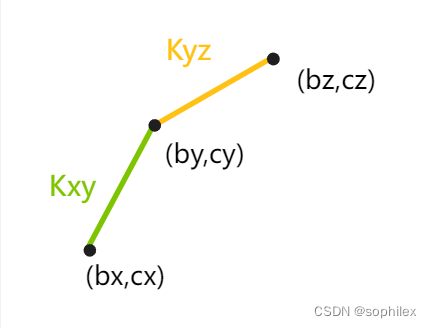
即: c y − c x b y − b x ≤ − a i \large \frac{c_y-c_x}{b_y-b_x}\leq -a_i by−bxcy−cx≤−ai(注意之前我们假定 b i b_i bi是单增的)
这里是在做一个参变分离,注意这里我们其实是将x,y的信息视为已知量,而将i作为变量
放到二维坐标系下考虑,就是 ( b x , c x ) , ( b y , c y ) (b_x,c_x),(b_y,c_y) (bx,cx),(by,cy)两个点的连线的斜率 ≤ − a i \leq -a_i ≤−ai
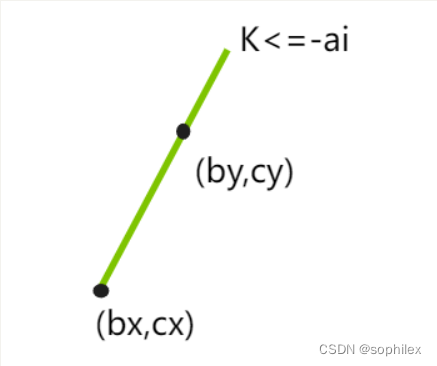
换句话说,这里如果x是y之前的比较优的一个点,在y出现之后它就被淘汰了,判断的条件我们记为 k x y < = K ( X ) k_{xy}<=K(X) kxy<=K(X),其中 K ( X ) = − a i K(X)=-a_i K(X)=−ai。
接着我们将考虑的点数扩大到三个点 x ≤ y ≤ z x\leq y \leq z x≤y≤z,这里我们不妨先限定 K y z ≤ K x y K_{yz}\leq K_{xy} Kyz≤Kxy
边界条件还是 K ( X ) = − a i K(X)=-a_i K(X)=−ai
按照之前的讨论,对于两个点 x , y x,y x,y,若 k x , y ≤ K ( x ) k_{x,y}\leq K(x) kx,y≤K(x),则点 y 优于 x y优于x y优于x,否则 点 x 优于 y 点x优于y 点x优于y
那么我们有如下几种情况:
- K y z < K x y ≤ K ( X ) K_{yz}<K_{xy} \leq K(X) Kyz<Kxy≤K(X),则点 z z z优于点 x , y x,y x,y
- K y z ≤ K ( X ) < K x y K_{yz}\leq K(X)<K_{xy} Kyz≤K(X)<Kxy,则点 x , z x,z x,z优于点 y y y
- K ( X ) ≤ K y z < K z y K(X)\leq K_{yz}<K_{zy} K(X)≤Kyz<Kzy,则点 x x x优于点 y , z y,z y,z
此时我们惊奇地发现,不管是哪一种情况,点 y y y都不可能作为最优解。按照之前所说,我们其实是对于这样一系列固定的点,对于不同的i,考察最优决策点的变化。也就是说,如果我们提前处理好了这样若干个点,那么我们就已经知道点y永远不会成为最优决策点了(在三个点都能选择的情况下)
讲回我们在这部分讨论前做的假设 K y z ≤ K x , y K_{yz}\leq K_{x,y} Kyz≤Kx,y,读者可以自行验证,当三点不满足该关系的时候,我们并不能得到类似或者什么更优的结论。
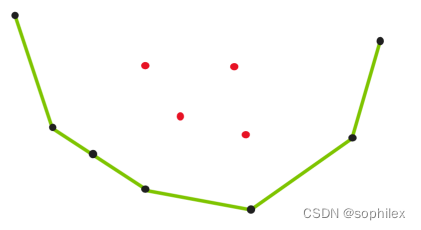
那么我们对于一个固定的点i,将所有能进行决策的点进行这样一个预处理过程的话(大部分情况下对于固定的点i,我们只能够在 [ 1 , i − 1 ] [1,i-1] [1,i−1]内决策,这里直接取该情况,其它情况其实同理), ∀ 1 ≤ x < y < z < i \forall 1\leq x<y<z< i ∀1≤x<y<z<i,若 K y z ≤ K x , y K_{yz}\leq K_{x,y} Kyz≤Kx,y,则将点y删除(因为它永远不会成为一个最优),那么将留下来的点两两按横坐标顺序前后链接,斜率是单调不降的,换句话说,留下来的点就形成了一个下凸包,如下图所示,其中绿色连接部分就是一个凸包,红色点是在处理过程中被删除的点
最优决策点的快速寻找
一旦要维护的东西变成了一个凸包,那么我们的手段就可以很骚了,因为此时它的斜率具有单调性,我们就可以上二分等手段了 😃
对于一个固定的i,我们有 K ( X ) = − a i K(X)=-a_i K(X)=−ai,由于下凸包的斜率是单增的,所以将斜率从左到右一一写出来的话,我们会得到如下关系
K 1 < K 2 < . . . < K s ≤ K ( X ) < K s + 1 . . . K m K_1<K_2<...<K_s\leq K(X)<K_{s+1}...K_{m} K1<K2<...<Ks≤K(X)<Ks+1...Km
那么我们要找的点显然就是s,也就是最后一个与前面的点连线的斜率 ≤ K ( X ) \leq K(X) ≤K(X)的点
那么我们维护好这个凸包之后,直接用二分线段即可,最后一个斜率 ≤ K ( X ) \leq K(X) ≤K(X)的线段的右端点就是答案了
考虑凸包的一个特殊情况:多个点处于一条线段上,就如上图的第二条线段,但是该情况对我们的选择并没有影响,因为我们取的是每一个线段的最右端点
这样每次去寻找最优决策点的复杂度是 O ( l o g ) O(log) O(log)的,再加上维护凸包的复杂度 O ( N ) O(N) O(N),时间复杂度就是 O ( N l o g N ) O(NlogN) O(NlogN)的
具体流程:
-
A 在凸包上二分找到最优决策点x
-
B 用x的值更新 d p i dp_i dpi
-
C 在将i加入凸包之前,我们要先将队尾一部分一定没有i优的点踢掉,然后再将i加入凸包
对步骤C的解释:这里将i直接加入凸包的话,有可能我们维护的就不再是一个凸包了,如下图情况
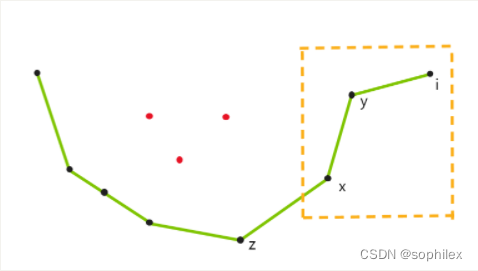
不难发现,此时 x , y , i x,y,i x,y,i三点形成的就是之前讨论过的三个点的情形,所以y是一定不会成为最优决策点的。同理,踢掉y之后,如果 z , x , i z,x,i z,x,i也是一个情况的话,x也会被踢掉,直到最后不再有这样的点为止
再优化
注意到上面的复杂度还是有点高,我们考虑dp过程中常见的决策单调性情况
决策单调性:在dp过程中,设 S i 表示 d p i S_i表示dp_i Si表示dpi的最优决策点,如果 ∀ i < j , S i ≤ S j \forall i<j,S_i\leq S_j ∀i<j,Si≤Sj则称该dp过程满足决策单调性,也就是说随着dp过程的进行,最优决策点是单调不降的
关于决策单调性的证明,常见的就是四边形不等式,这里暂且不提,后面有空再说:)
决策单调性在这里意味着什么?意味着之前已经被淘汰的点是不会再作为最优决策点出现的。所以我们就可以考虑用单调队列来维护。
具体流程:
- A 将队列首部斜率 ≤ K ( X ) \leq K(X) ≤K(X)的线段的左端点不断踢出,最后剩下的队首元素x就是最优决策点。(正确性显然)
- B 用x的值更新 d p i dp_i dpi
- C 在将i加入凸包之前,我们要先将队尾一部分一定没有i优的点踢掉,然后再将i加入凸包
与直接二分的区别就在于步骤A
同时我们注意到,如果 K ( X ) K(X) K(X)是单调的,其自然满足决策点的单调性。(在横坐标单调的前提下)
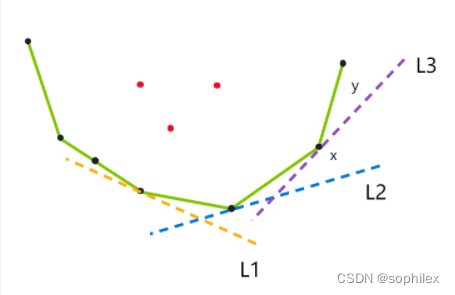
类型总结(单调队列维护凸包)
当dp式子满足 c y − c x b y − b x ≤ − a i \large \frac{c_y-c_x}{b_y-b_x}\leq -a_i by−bxcy−cx≤−ai的时候,我们要维护的是一个下凸包
ll hd=1,tl=0;
que[++tl]=0;
for(int i=1;i<=n;++i)
{
while(hd<tl&&Slope(que[hd],que[hd+1])<=k[x]) hd++;//这里k[x]表示K(X)
dp[i]=...//用que[hd]来更新dp[i]即可
while(hd<tl&&Slope(que[tl-1],que[tl])>=Slope(que[tl],i)) tl--;
que[++tl]=i;//插入凸包
}
当dp式子满足 c y − c x b y − b x ≥ − a i \large \frac{c_y-c_x}{b_y-b_x}\geq -a_i by−bxcy−cx≥−ai的时候,同理就是维护一个上凸包
ll hd=1,tl=0;
que[++tl]=0;
for(int i=1;i<=n;++i)
{
while(hd<tl&&Slope(que[hd],que[hd+1])>=k[x]) hd++;//这里k[x]表示K(X)
dp[i]=...//用que[hd]来更新dp[i]即可
while(hd<tl&&Slope(que[tl-1],que[tl])<=Slope(que[tl],i)) tl--;
que[++tl]=i;//插入凸包
}
Tip
- 当两个点的横坐标相等的时候,实际上不存在斜率,这里我们要特判,取为inf
- 到底维护的是上凸包还是下凸包不要弄混,仔细推导一遍最好
- 一般是直接用double类型来计算斜率并进行比较,但是有时候出题人不讲武德卡精度,那就要转成乘式类型来比较了,这时候要注意一下负号改变方向的情况
- 队列一开始要放进去一个0,毕竟也不一定非有上一个转移点
- 有时候dp值会需要预处理,要小心
- 比较斜率的时候最好使用 ≤ , ≥ \leq,\geq ≤,≥
一些特殊情况
- b j b_j bj是单调减的:实际与之前的情况同理。在一开始的推导中我们假定 x < y x<y x<y,本质上就是为了保证 b j b_j bj是单增的,如果此时它是单减的,我们只要在原本的式子中在对应位置取负,再改变前面符号,重新推导即可。此时 − b j -b_j −bj就是单增的了
- b j b_j bj不具备单调性:此时我们不能直接通过单调队列来维护凸包,因为新加入的点的横坐标并不是单调的,可能会插入在凸包的中间的位置。此时需要采用cdq分治
- 不具备决策单调性:那就只能二分了,不能强行弹出点,因为它可能在后面会成为最优决策点
- 不具备决策单调性&横坐标不单调:cdq分治 后面会讲
例子
仓库建设
大意:
n n n 个工厂,由高到低分布在一座山上,工厂 1 1 1 在山顶,工厂 n n n 在山脚。第 i i i 个工厂目前已有成品 p i p_i pi 件,在第 i i i 个工厂位置建立仓库的费用是 c i c_i ci。对于没有建立仓库的工厂,其产品应被运往其他的仓库进行储藏,产品只能往山下运(即只能运往编号更大的工厂的仓库),一件产品运送一个单位距离的费用是 1 1 1。
- 工厂 i i i 距离工厂 1 1 1 的距离 x i x_i xi(其中 x 1 = 0 x_1=0 x1=0)。
- 工厂 i i i 目前已有成品数量 p i p_i pi。
- 在工厂 i i i 建立仓库的费用 c i c_i ci。
问修建仓库的最小代价
思路:
设 d p i dp_i dpi表示前i个工厂的最小代价,写出dp式子的过程还是比较套路的,
d p i = m i n j ≤ i { d p j + x i ∑ k = j + 1 i ( p k ) − ∑ k = j + 1 i ( x k p k ) } + c i dp_i=min_{j\leq i}\{dp_j+x_i\sum_{k=j+1}^{i}(p_k)-\sum_{k=j+1}^{i}(x_kp_k) \}+c_i dpi=minj≤i{dpj+xi∑k=j+1i(pk)−∑k=j+1i(xkpk)}+ci
转化得到
d p i = m i n j ≤ i { d p j + x i ( s u m i − s u m j ) − ( x s u m i − x s u m j ) } + c i dp_i=min_{j\leq i}\{dp_j+x_i(sum_i-sum_j)-(xsum_i-xsum_j)\}+c_i dpi=minj≤i{dpj+xi(sumi−sumj)−(xsumi−xsumj)}+ci
其中 s u m i = ∑ k = 1 i p k , x s u m i = ∑ k = 1 i p k ∗ x k sum_i=\sum_{k=1}^{i}p_k,xsum_i=\sum_{k=1}^{i}p_k*x_k sumi=∑k=1ipk,xsumi=∑k=1ipk∗xk
所以 d p i = m i n j ≤ i { − s u m j x i + ( d p j + x s u m j ) } + x i s u m i − x s u m i + c i dp_i=min_{j\leq i}\{-sum_jx_i+(dp_j+xsum_j)\}+x_isum_i-xsum_i+c_i dpi=minj≤i{−sumjxi+(dpj+xsumj)}+xisumi−xsumi+ci
这里 s u m j sum_j sumj是单调增的
考虑 a < y b a<yb a<yb,且b优于a:
令 f j = d p j + x s u m j f_j=dp_j+xsum_j fj=dpj+xsumj
− s u m b x i + f b ≤ − s u m a x i + f a -sum_bx_i+f_b\leq -sum_ax_i+f_a −sumbxi+fb≤−sumaxi+fa
f b − f a s u m b − s u m a ≤ x i \frac{f_b-f_a}{sum_b-sum_a}\leq x_i sumb−sumafb−fa≤xi,这里我们要维护的就是一个下凸包了,并且斜率 K ( X ) = x i K(X)=x_i K(X)=xi是单调增的
因此直接套板子即可
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=1e6+10;
const ll inf=1e18;
struct ty
{
ll x,p,c;
}mas[N];
ll sum[N];
ll xsum[N];
ll n;
ll dp[N];
ll que[N];
ll gt(ll l,ll r)
{
return mas[r].x*(sum[r]-sum[l])-(xsum[r]-xsum[l]);
}
double Slope(ll a,ll b)
{
if(sum[a]==sum[b]) return inf;
double x=(dp[a]+xsum[a]-dp[b]-xsum[b])*1.0;
double y=(sum[a]-sum[b])*1.0;
return x/y;
}
void solve()
{
cin>>n;
for(int i=1;i<=n;++i) cin>>mas[i].x>>mas[i].p>>mas[i].c;
for(int i=1;i<=n;++i) sum[i]=sum[i-1]+mas[i].p,xsum[i]=xsum[i-1]+mas[i].x*mas[i].p;
ll hd=1,tl=0;
que[++tl]=0;
for(int i=1;i<=n;++i)
{
while(hd<tl&&Slope(que[hd],que[hd+1])<mas[i].x) hd++;
dp[i]=dp[que[hd]]+gt(que[hd],i)+mas[i].c;
while(hd<tl&&Slope(que[tl-1],que[tl])>Slope(que[tl],i)) tl--;
que[++tl]=i;
}
ll pos=n;
while(mas[pos].p==0) pos--;
ll ans=inf;
for(int i=pos;i<=n;++i) ans=min(ans,dp[i]);
cout<<ans<<endl;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}
PS:此题有其它坑点,读者自己小心~
[USACO08MAR] Land Acquisition G
大意:
将 n n n块土地分组,每组的价格是这组土地中最大的长宽乘积,问买下所有土地的最小花费。
思路:
个人感觉一开始的思路还是有点妙的
不妨按照长升序排序,如果长相同就宽升序
从前往后遍历的时候,考虑 i < j i<j i<j,显然如果 i , j i,j i,j放一组,长一定是取 j j j的,那么如果 j j j的宽也大于 i i i的话,那么 i i i就没有任何贡献。所以我们可以用一个栈来维护,把没用的东西踢掉。显然在最优决策下,每一组的土地会是连续的一段
考虑 d p i dp_i dpi表示排序弹出处理之后前i个土地的最小值:
d p i = m i n j ≤ i { d p j + b j + 1 a i } dp_i=min_{j\leq i}\{dp_j+b_{j+1}a_i\} dpi=minj≤i{dpj+bj+1ai},其中 a a a表示长, b b b表示宽
这里 b j b_j bj在处理之后是降序的,我们可以转化成 d p i = m i n j ≤ i { d p j − b j + 1 ′ a i } , b j ′ = − b j dp_i=min_{j\leq i}\{dp_j-b'_{j+1}a_i\},b'_j=-b_j dpi=minj≤i{dpj−bj+1′ai},bj′=−bj
考虑 x < y x<y x<y,且y优于x
− b y ′ a i + d p j ≤ − b x ′ a i + d p x -b'_ya_i+dp_j\leq -b'_xa_i+dp_x −by′ai+dpj≤−bx′ai+dpx
d p x − d p y b x ′ − b y ′ ≤ a i \frac{dp_x-dp_y}{b'_x-b'_y}\leq a_i bx′−by′dpx−dpy≤ai,还是维护一个下凸包,并且斜率 a i a_i ai是单增的,所以也是直接套板子
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=1e6+10;
const ll inf=1e18;
struct ty
{
ll a,b;
bool operator <(const ty & B) const
{
if(a==B.a) return b<B.b;
return a<B.a;
}
}mas[N];
ll n;
ll que[N];
ll dp[N];
ty st[N];
ll top=0;
double Slope(ll x,ll y)
{
if(st[x+1].b==st[y+1].b) return inf;
return 1.0*((dp[y]-dp[x])/(-st[y+1].b+st[x+1].b));
}
void solve()
{
cin>>n;
for(int i=1;i<=n;++i)
{
cin>>mas[i].a>>mas[i].b;
}
sort(mas+1,mas+1+n);
for(int i=1;i<=n;++i)
{
while(top)
{
if(mas[i].b>=st[top].b) top--;
else break;
}
st[++top]=mas[i];
}
ll hd=1,tl=0;
que[++tl]=0;
for(int i=1;i<=top;++i)
{
while(hd<tl&&Slope(que[hd],que[hd+1])<st[i].a) hd++;
// cout<<i<<" "<<que[hd]<<endl;
dp[i]=dp[que[hd]]+st[que[hd]+1].b*st[i].a;
while(hd<tl&&Slope(que[tl-1],que[tl])>Slope(que[tl],i)) tl--;
que[++tl]=i;
}
cout<<dp[top]<<endl;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}
[ZJOI2007]仓库建设
大意:
本人太懒。。。
思路:
这题就是需要cdq分治的题了
考虑 f i f_i fi表示第i天能够获得的最大钱数, g i g_i gi表示第i天最多能买多少张B券
则 g i = f i r i a i + b i \large g_i=\frac{f_i}{r_ia_i+b_i} gi=riai+bifi
故 f i = m a x { m a x j ≤ i − 1 { g j b i a i + r j g j } ∗ a i , f i − 1 } f_i=max\{max_{j\leq i-1}\{g_j\frac{b_i}{a_i}+r_jg_j\}*a_i,f_{i-1}\} fi=max{maxj≤i−1{gjaibi+rjgj}∗ai,fi−1}
外层的max我们可以直接特判,内层的max就是一个典型的斜率优化dp了。
考虑 g x < g y g_x<g_y gx<gy,且y优于x(这里 g g g不是单调的,我们不能直接假设 x < y x<y x<y),l令 F j = r j g j F_j=r_jg_j Fj=rjgj
g x b i a i + F x ≥ g y b i a i + F y g_x\frac{b_i}{a_i}+F_x\geq g_y\frac{b_i}{a_i}+F_y gxaibi+Fx≥gyaibi+Fy
即 F x − F y g x − g y ≤ − b i a i \large \frac{F_x-F_y}{g_x-g_y}\leq -\frac{b_i}{a_i} gx−gyFx−Fy≤−aibi
实际还是一个下凸包。这里横坐标是 g j g_j gj,纵坐标是 F j F_j Fj,斜率是 − b i a i -\frac{b_i}{a_i} −aibi
横坐标不是单调的,斜率也不是单调的,看起来不是能用普通凸包来维护的样子。所以我们可以使用cdq分治
想要用单调队列维护凸包的话,我们实际上有三维偏序:
- 对于每一个i,它的决策点是 { j ∣ j < i } \{j|j<i\} {j∣j<i},也就是id较小的点才可以更新id较大的点
- 维护凸包的时候,如果x先于y加入凸包,要满足 g x < g y g_x<g_y gx<gy
- 凸包查询最优决策点的时候,如果x先于y查询,要满足 K ( x ) < K ( y ) K(x)<K(y) K(x)<K(y),因为我们要利用决策点不降的性质来加速选择最优点的过程
显然,三维偏序正是cdq分治的拿手好戏~
- 第一关键字:首先将点按照斜率升序排序,能够保证查询的斜率递增,从而能用单调队列维护
- 第二关键字:分治时按照id分成左右两个部分。这样保证最后递归到叶子节点的时候是符合原本顺序的,且斜率查询的时候保证都是维护的点的id都是在自己之前的(其实就是一个归并排序)
- 第三关键字:x 每次分治结束之后内部不再有贡献,所以我们可以直接按照横坐标升序排序方便后面维护凸包
我们会发现这样处理之后就能够实现三维偏序了。
cdq分治的灵魂是用前半部分的信息来统计对后半部分的贡献,当一段区间分治结束之后,这段区间内的信息就全部处理完了,换句话说,区间内部的点之间是不会再产生贡献了,因此我们才可以随意更改该区间内部的点的顺序。将其按照横坐标排序,我们才能进行凸包的维护。同时,以横坐标为关键字的排序我们可以直接sort,但是也可以采用归并排序
最后,求出 f i f_i fi之后,再与 f i − 1 取 m a x f_{i-1}取max fi−1取max,并更新 g i g_i gi
具体流程:
- if(l==r) 更新,退出
- 按照id分成左右两部分 [ l , m i d ] , ( m i d , r ] [l,mid],(mid,r] [l,mid],(mid,r]
- cdq(l,mid)
- 此时 [ l , m i d ] [l,mid] [l,mid]已经处理好了,所以用单调队列对 [ l , m i d ] [l,mid] [l,mid]建凸包
- ( m i d , r ] (mid,r] (mid,r]区间此时是以 − b i a i \frac{-b_i}{a_i} ai−bi升序,所以按顺序更新即可,并更新凸包
- cdq(mid+1,r)
- 按照横坐标对 [ l , r ] [l,r] [l,r]进行归并,因为该区间内部不会再有互相的贡献了
#include <bits/stdc++.h>
#define pii pair<int,int>
#define il inline
#define ll long long
#define double long double
const double eps =1e-8;
using namespace std;
const int N=1e5+10;
const ll inf=1e17;
ll n;
double s;
double A[N],B[N],R[N];
double f[N],X[N];
struct ty
{
ll id;
double slope;
double a,b,k;
//第一关键字:斜率 按照斜率升序能够保证查询的斜率递增,从而能用单调队列维护
//第二关键字:id 分治时按照id分成左右两个部分。这样保证最后递归到叶子节点的时候是符合原本顺序的
//且斜率查询的时候保证都是维护的点的id都是在自己之前的
//第三关键字:x 每次分治结束之后内部不再有贡献,则按照x升序排方便后面维护凸包
bool operator <(const ty & b) const
{
if(slope==b.slope) return id<b.id;
return slope>b.slope;//斜率递减
}
}mas[N],tmp[N];
ll que[N];
double Slope(ll x,ll y)
{
if(X[mas[x].id]==X[mas[y].id])
{
return inf;
}
return (X[mas[y].id]*mas[y].k-X[mas[x].id]*mas[x].k)/(X[mas[y].id]-X[mas[x].id]);
}
void upd(int id,double val)
{
if(f[mas[id].id]<val)
{
f[mas[id].id]=val;
X[mas[id].id]=f[mas[id].id]/(mas[id].k*mas[id].a+mas[id].b);
}
}
void cdq(ll l,ll r)
{
if(l==r)
{
f[mas[l].id] = max(f[mas[l].id],f[mas[l].id-1]);//这里的f_{i-1}是所有排序前的i-1,所以要稍微绕一下,注意别弄错
X[mas[l].id]=f[mas[l].id]/(mas[l].k*mas[l].a+mas[l].b);
return;
}
ll mid=(l+r)>>1;
ll posl=l,posr=mid+1;
for(int i=l;i<=r;++i)
{
if(mas[i].id<=mid) tmp[posl++]=mas[i];
else tmp[posr++]=mas[i];
}
for(int i=l;i<=r;++i) mas[i]=tmp[i];
//按照id处理好了
cdq(l,mid);
//先处理前一个部分,保证此时前半部分的x是升序的
ll hd=1,tl=0;
for(int i=l;i<=mid;++i)//维护凸包
{
while(tl>hd&&Slope(que[tl-1],que[tl])<Slope(que[tl],i)+eps) tl--;
que[++tl]=i;
}
ll id;
for(int i=mid+1;i<=r;++i)//计算两边产生的贡献
{
while(tl>hd&&Slope(que[hd],que[hd+1])>mas[i].slope) hd++;
upd(i,X[mas[que[hd]].id]*(mas[que[hd]].k-mas[i].slope)*mas[i].a);
}
cdq(mid+1,r);
posl=l,posr=mid+1;
ll tot=l-1;
while(posl<=mid&&posr<=r)
{
if(X[mas[posl].id]<X[mas[posr].id]) tmp[++tot]=mas[posl++];
else tmp[++tot]=mas[posr++];
}
while(posl<=mid) tmp[++tot]=mas[posl++];
while(posr<=r) tmp[++tot]=mas[posr++];
for(int i=l;i<=r;++i) mas[i]=tmp[i];
}
void solve()
{
cin>>n>>s;
for(int i=1;i<=n;++i)
{
cin>>A[i]>>B[i]>>R[i];
mas[i].id=i;
mas[i].a=A[i];mas[i].b=B[i];mas[i].k=R[i];
mas[i].slope=-B[i]/A[i];
// if(i>1) continue;
X[mas[i].id]=s/(R[i]*A[i]+B[i]);
// mas[i].y=R[i]*mas[i].x;
}
for(int i=1;i<=n;++i) f[i]=s;
sort(mas+1,mas+1+n);
cdq(1,n);
cout<<fixed<<setprecision(4)<<f[n]<<endl;
}
int main()
{
// freopen("1.out","w",stdout);
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}
后记
斜率优化dp在大部分情况下都是结合决策单调性进行的(大部分),所以也比较套路
另外还有结合Wqs二分来处理前n个数限定分m段的情况等的套路,个人感觉决策单调性优化的水还是有点深的,有空会试试写一期总结
加油~