一、题目

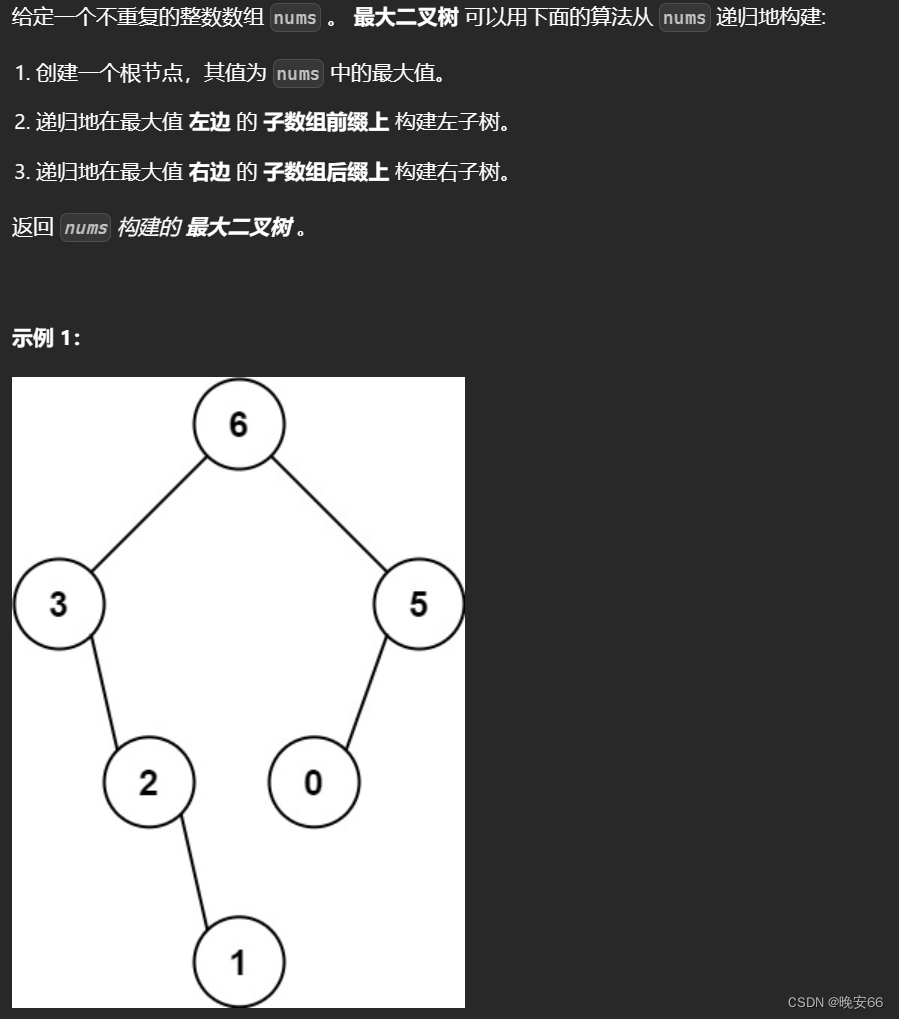
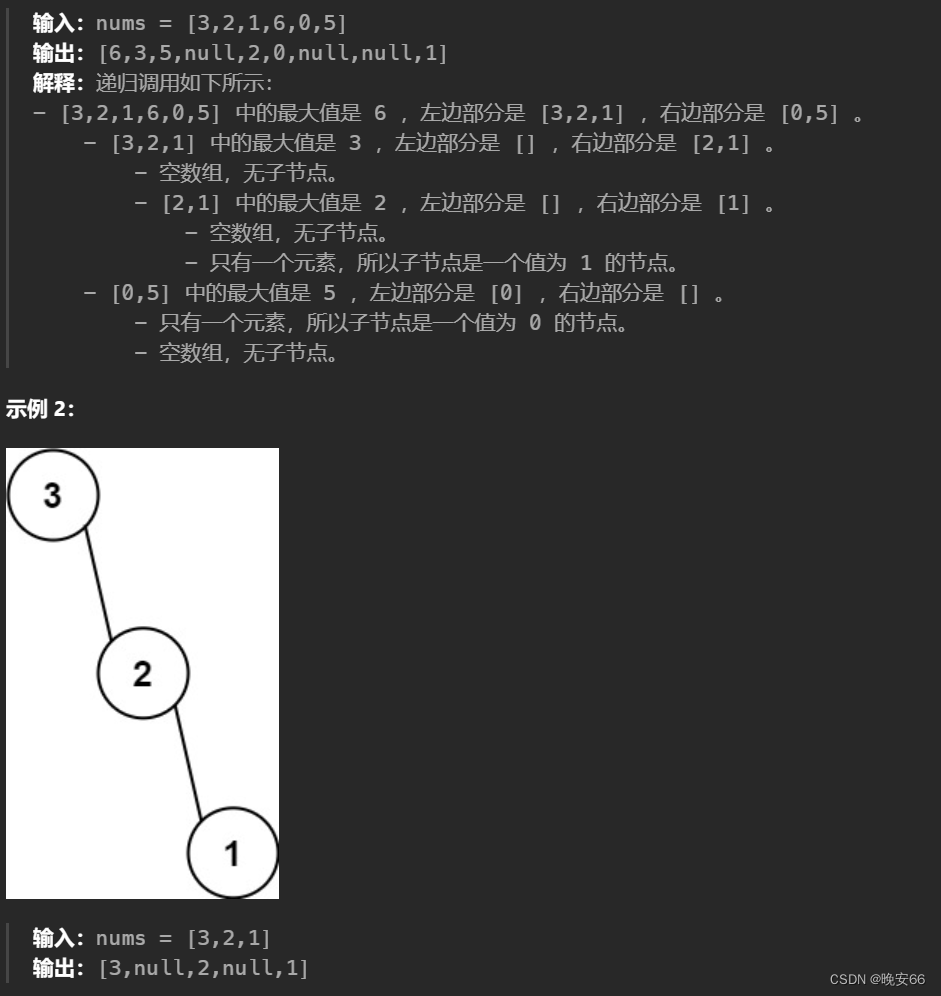
在这里插入图片描述

二、解法

思路分析：【算法与数据结构】106、LeetCode从中序与后序遍历序列构造二叉树这两道题有些类似，相关代码可以互相参考，本题明示了要用递归来做，那么递归三要素不可缺少：输入参数和返回值；单层递归逻辑；终止条件。本题当中，输入参数引用二叉树遍历数组，同时根据最大值划分的边界[Begin, End)，代码统一为左闭右开区间，区间具体如何划分设计到边界条件是否+1-1这种。返回值为root根节点。
程序如下：

class Solution {
public:
    // 3、输入参数
    TreeNode* traversal(const vector<int> &nums, int Begin, int End) {
        // 1、终止条件
        if (Begin == End) return NULL;

        //2、单层递归逻辑
        int maxIndex = Begin;
        for (int i = Begin; i < End; i++) { // 找最大值
            if (nums[i] > nums[maxIndex]) maxIndex = i;
        }
        TreeNode* root = new TreeNode(nums[maxIndex]);

        // 最大值左边部分，左闭右开[leftBegin, leftEnd)
        int leftBegin = Begin; 
        int leftEnd = maxIndex;
        if (leftEnd < leftBegin) leftEnd = Begin;

        // 最大值右边部分，左闭右开[rightBegin, rightEnd)
        int rightBegin = maxIndex + 1;
        int rightEnd = End;
        if (rightBegin > rightEnd) rightBegin = End;
        

        root->left = traversal(nums, leftBegin, leftEnd);
        root->right = traversal(nums, rightBegin, rightEnd);

        // 3、返回值
        return root;
    }

	TreeNode* constructMaximumBinaryTree(vector<int>& nums) {  
        if (!nums.size()) return NULL;
        return traversal(nums, 0, nums.size());
	}
};

三、完整代码

# include <iostream>
# include <vector>
# include <queue>
using namespace std;

// 树节点定义
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    // 3、输入参数
    TreeNode* traversal(const vector<int> &nums, int Begin, int End) {
        // 1、终止条件
        if (Begin == End) return NULL;

        //2、单层递归逻辑
        int maxIndex = Begin;
        for (int i = Begin; i < End; i++) { // 找最大值
            if (nums[i] > nums[maxIndex]) maxIndex = i;
        }
        TreeNode* root = new TreeNode(nums[maxIndex]);

        // 最大值左边部分，左闭右开[leftBegin, leftEnd)
        int leftBegin = Begin; 
        int leftEnd = maxIndex;
        if (leftEnd < leftBegin) leftEnd = Begin;

        // 最大值右边部分，左闭右开[rightBegin, rightEnd)
        int rightBegin = maxIndex + 1;
        int rightEnd = End;
        if (rightBegin > rightEnd) rightBegin = End;
        

        root->left = traversal(nums, leftBegin, leftEnd);
        root->right = traversal(nums, rightBegin, rightEnd);

        // 3、返回值
        return root;
    }

	TreeNode* constructMaximumBinaryTree(vector<int>& nums) {  
        if (!nums.size()) return NULL;
        return traversal(nums, 0, nums.size());
	}
};

// 层序遍历
vector<vector<int>> levelOrder(TreeNode* root) {
    queue<TreeNode*> que;
    if (root != NULL) que.push(root);
    vector<vector<int>> result;
    while (!que.empty()) {
        int size = que.size();  // size必须固定, que.size()是不断变化的
        vector<int> vec;
        for (int i = 0; i < size; ++i) {
            TreeNode* node = que.front();
            que.pop();
            vec.push_back(node->val);
            if (node->left) que.push(node->left);
            if (node->right) que.push(node->right);
        }
        result.push_back(vec);
    }
    return result;
}

template<class T1, class T2>
void my_print2(T1& v, const string str) {
    cout << str << endl;
    for (class T1::iterator vit = v.begin(); vit < v.end(); ++vit) {
        for (class T2::iterator it = (*vit).begin(); it < (*vit).end(); ++it) {
            cout << *it << ' ';
        }
        cout << endl;
    }
}

int main()
{
    //int arr[] = {3, 2, 1, 6, 0, 5};
    int arr[] = { 3, 2, 1};
    vector<int> nums(arr, arr + sizeof(arr) / sizeof(int));

    Solution s;
    TreeNode* root = s.constructMaximumBinaryTree(nums);

    vector<vector<int>> tree = levelOrder(root);
    my_print2<vector<vector<int>>, vector<int>>(tree, "目标树:");

	system("pause");
	return 0;
}