300. 最长递增子序列
leetcode链接:力扣题目链接
视频链接:动态规划之子序列问题,元素不连续!| LeetCode:300.最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。
例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
输入:nums = [0,1,0,3,2,3]
输出:4
示例 3:
输入:nums = [7,7,7,7,7,7,7]
输出:1
首先我们明确一下子序列的定义,子序列与子串(必须要连续)不同,子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。
动规五部曲
- 确定dp数组含义及下标
dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度。
这里明确dp[i]的含义很重要,因为这道题我们返回的结果不一定是dp[n - 1],而是dp中最大的一个,因为最长的序列不一定以nums[i]结尾。
- 确定dp数组的递推公式
考虑下面的情景,假设我们已经知道了 dp[0..4] 的所有结果,我们如何通过这些已知结果推出 dp[5] 呢?

想法就是如果前面的数比nums[i]小,那就是递增的,可以加入候选,我们取前面最大的加1,接到nums[i]上去,就是最长的子序列。使用两层for循环。
- dp数组的初始化
每个dp[i]即子序列长度最小都是1。
- 确定遍历顺序
没什么好说的,从前往后。
- 打印dp数组
最终代码;
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
vector<int> dp(nums.size(), 1);
int res = 0;
for(int i = 0; i < nums.size(); i++){
for(int j = 0; j < i; j++){
if(nums[i] > nums[j]){
dp[i] = max(dp[j] + 1,dp[i]);
}
}
res = dp[i] > res ? dp[i] : res;
}
//这里注意不是return dp[n - 1]了,牢记dp的含义;
//return dp[nums.size() - 1];
//return *max_element(dp.begin(),dp.end());
return res;
}
};
674. 最长连续递增序列(这题反而是easy难度)
leetcode链接:力扣题目链接
视频链接:动态规划之子序列问题,重点在于连续!| LeetCode:674.最长连续递增序列
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
示例 1:
输入:nums = [1,3,5,4,7]
输出:3
解释:最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
示例 2:
输入:nums = [2,2,2,2,2]
输出:1
解释:最长连续递增序列是 [2], 长度为1。
首先是贪心解法,只要nums[i+1]比nums[i]就记录,然后取最大的:
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
int len = 1, maxLen = 1;
for(int i = 0; i < nums.size() - 1; i++){
if(nums[i + 1] > nums[i] ){
len++;
}else{
maxLen = len > maxLen ? len : maxLen;
cout<< maxLen<< ' ';
len = 1;
}
}
maxLen = len > maxLen ? len : maxLen;
return maxLen;
}
};
动规五部曲
- 确定dp数组下标及其含义
dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度。
返回的也是dp[i]中最大的那个。
- 确定递推公式
如果nums[i] > nums[i - 1],可以接上,即dp [i] = nums[i - 1] + 1。
如果不成立,中断,dp[i] = 1;
- dp数组的初始化
每个都初始化为1;
- 遍历顺序
显然是从左往右遍历。
- 打印dp数组
最终代码:
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
if (nums.size() == 0) return 0;
int result = 1;
vector<int> dp(nums.size() ,1);
for (int i = 1; i < nums.size(); i++) {
if (nums[i] > nums[i - 1]) { // 连续记录
dp[i] = dp[i - 1] + 1;
}
if (dp[i] > result) result = dp[i];
}
return result;
}
};
718. 最长重复子数组
leetcode链接:力扣题目链接
视频链接:动态规划之子序列问题,想清楚DP数组的定义 | LeetCode:718.最长重复子数组
给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。
示例 1:
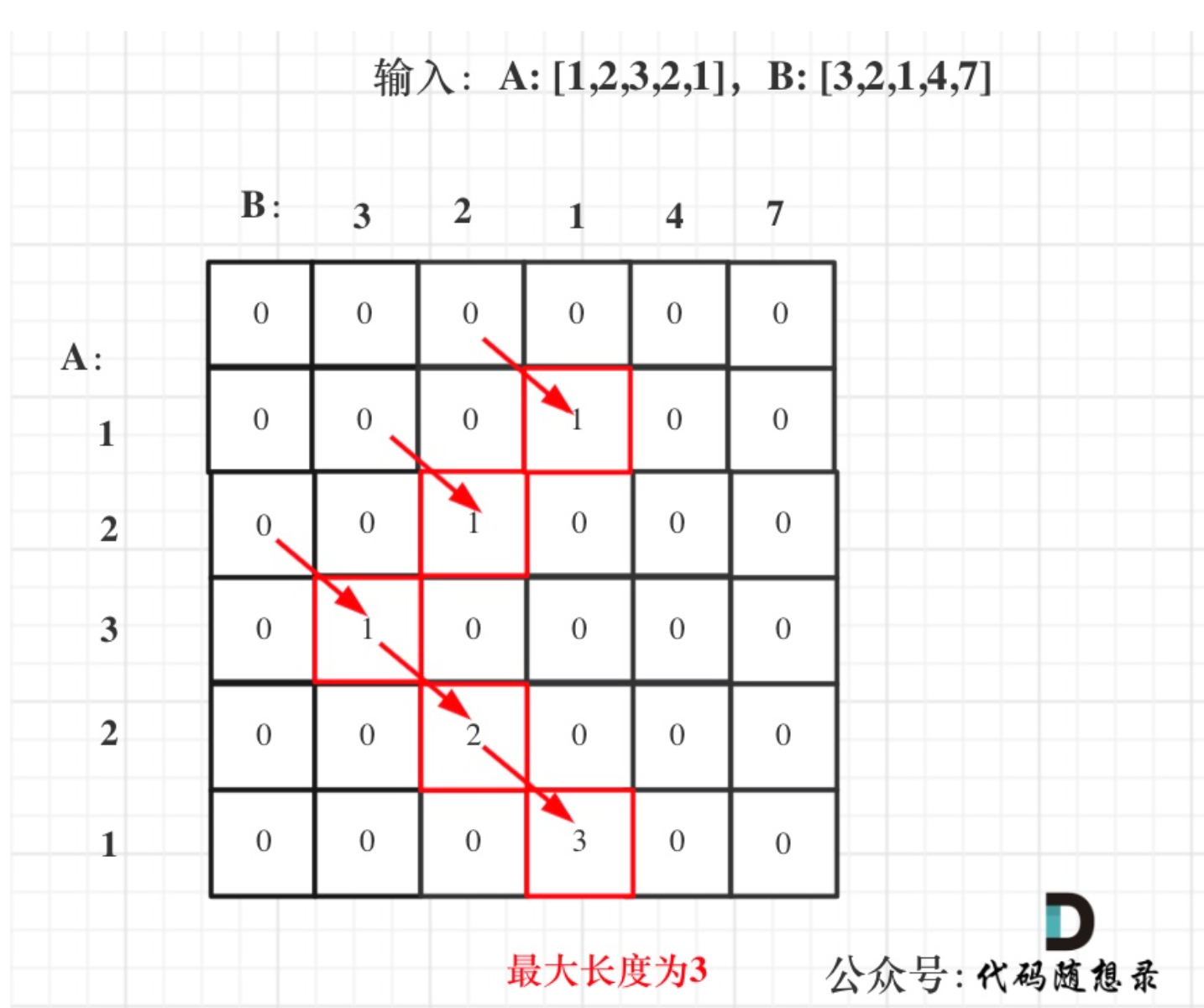
输入:nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出:3
解释:长度最长的公共子数组是 [3,2,1] 。
示例 2:
输入:nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
输出:5
这里要明确一下子数组的含义,注意题目中说的子数组,其实就是连续子序列。
如果用暴力,就是把所有的子序列都穷举出来,进行比较,这里复杂度太高肯定没办法AC。考虑动态规划算法。
动规五部曲
- 确定dp数组下标及其含义
dp[i][j] :以下标i - 1为结尾的A,和以下标j - 1为结尾的B,最长重复子数组长度为dp[i][j]。 (特别注意: “以下标i - 1为结尾的A” 标明一定是 以A[i-1]为结尾的字符串 )
故此时dp[0][0]无意义,遍历都从dp[1][1]开始。
最后返回的是dp[i][j]中的最大值。
- 确定递推公式
如果A[i - 1]和B[j - 1]相等,那么dp[i][j] = dp[i -1][j - 1](接上了),
- dp数组的初始化
根据dp[i][j]的定义,dp[i][0] 和dp[0][j]其实都是没有意义的!
但dp[i][0] 和dp[0][j]要初始值,因为 为了方便递归公式dp[i][j] = dp[i - 1][j - 1] + 1;
所以dp[i][0] 和dp[0][j]初始化为0。
- 遍历顺序
外层for循环遍历A,内层for循环遍历B。同时在遍历时把dp[i][j]的最大值记录下来。
- 打印dp数组
最终代码:
class Solution {
public:
int findLength(vector<int>& nums1, vector<int>& nums2) {
vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1,0));
int res = 0;
for(int i = 1; i <= nums1.size();i++){
for(int j = 1; j <= nums2.size(); j++) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
if (dp[i][j] > res) {
res = dp[i][j];
}
}
}
return res;
}
};
- 时间复杂度:O(n × m),n 为A长度,m为B长度
- 空间复杂度:O(n × m)
总结
- 注意返回值不一定都是dp数组的最后一个,要留意dp数组含义和题意看看留dp中的哪个
- 可以在最后进行处理,也可以在运行过程中处理,建议在dp定下来的时候就处理。