【算法】递归的概念、基本思想

news2025/1/16 6:33:45

创作不易，本篇文章如果帮助到了你，还请点赞关注支持一下♡>𖥦<)!!
主页专栏有更多知识，如有疑问欢迎大家指正讨论，共同进步！
🔥c++系列专栏：C/C++零基础到精通 🔥

给大家跳段街舞感谢支持！ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ

在这里插入图片描述

c语言内容💖：

专栏：c语言之路重点知识整合

【c语言】全部知识点总结

一、递归的概念

递归（Recursion）：是一个函数在其定义中直接或间接调用自身的一种方法。直接或间接地调用自身的算法称为递归算法。用函数自身给出定义的函数称为递归函数。

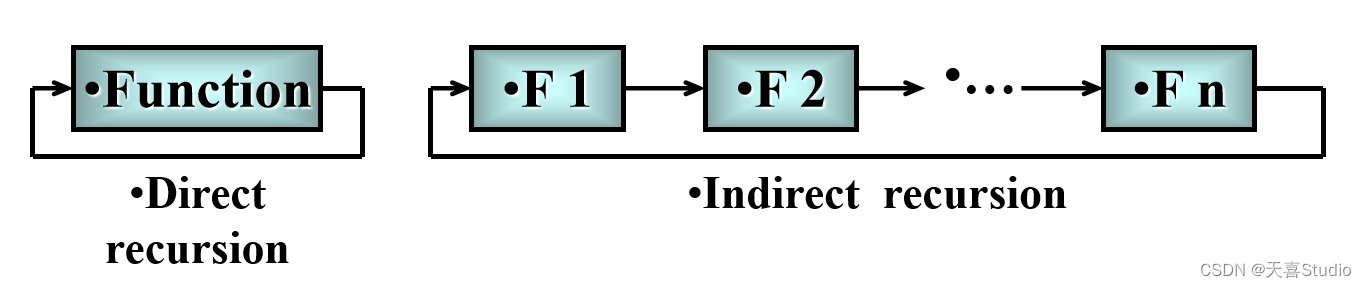
在这里插入图片描述

递归算法通过函数调用自身将问题转化为本质相同但规模较小的子问题，是分治策略的具体体现

递归需要有递归出口与递归关系式：

递归出口：边界条件，停止递归，问题规模足够小，直可以接给出答案
递归关系式：分解原问题为更小规模但解决方法与原问题一样的子问题

1）例：阶乘

int factorial(int n)
{
    if (n == 0) return 1; 		//递归出口
    return n * factorial(n − 1);    //递归关系式
}

阶乘函数可递归地定义为：

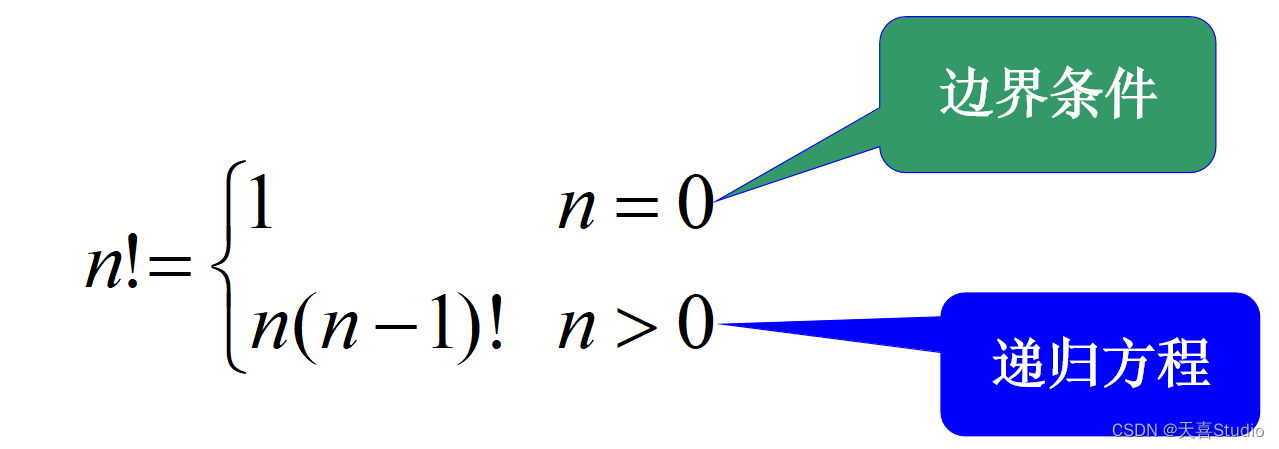
在这里插入图片描述

边界条件与递归方程是递归函数的两个要素，递归函数只有具备了这两个要素，才能在有限次计算后得出结果

总结枚举设计的递归函数的基本框架： 当问题规模小到可以直接解决

type method(数据)
{
   if(问题规模足够小）
   {
       输出结果;  	 //递归出口
   }
   else{
       分解问题为更小规模的子问题;   //递归关系式
   }
  }

2）例：斐波那契数列

无穷数列1，1，2，3，5，8，13，21，34，55，……，称为Fibonacci数列。它可以递归地定义为：

在这里插入图片描述

int Fibonacci(int n)
{
    if (n <= 1) 
        return 1;
    return Fibonacci(n-1)+Fibonacci(n-2);
}

3）例：汉诺塔问题

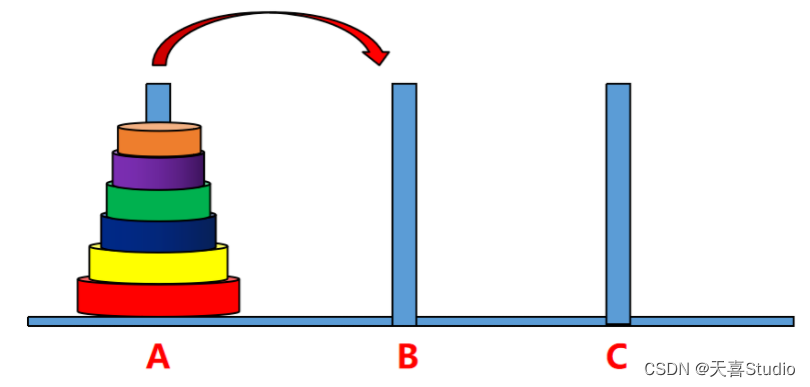
汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

见文章：【c语言习题】函数递归调用实现汉诺塔

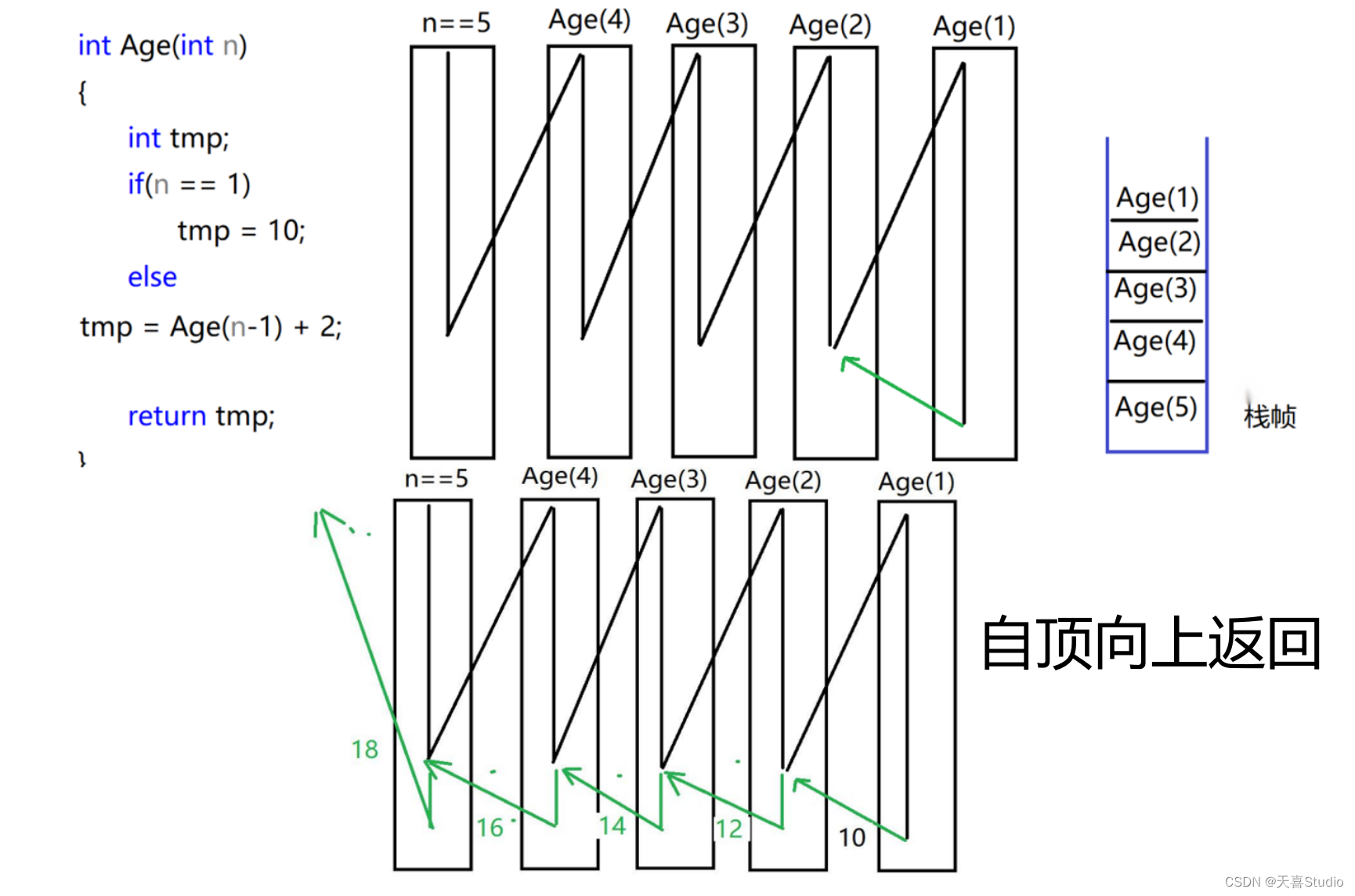
在这里插入图片描述