九、idSpanMap使用基数树代替原本的unordered_map
我们原本的idSpanMap用的是STL容器中的unordered_map哈希桶,因为STL的容器本身是不保证线程安全的,所以我们在访问时需要加锁保证线程安全,这也就是我们写的内存池的性能的瓶颈点。因为我做的这个内存池的项目是参照谷歌的开源项目tc-malloc,然后自主实现的mini版本,我查看tc-malloc的源码的优化策略是利用一颗基数树来代替stl中的unordered_map的,因为我们的需求是要保存页号和Span的映射关系,Span是指针本质也是一个整数,也就是说我们要保存的是<int,int>的映射关系,而基数树正好可以满足我们的需求,所以基数树就成为了优化我们的内存池的不二人选,并且用这个基数树定义idSpanMap最大的好处是访问idSpanMap时不需要加锁也能保证线程安全的。那它是怎么做到的呢?接下来我们就来学习一下。
9.1 什么是基数树?
基数树说白了也是一种哈希结构,基数树分为一层基数树,两层基数树,三层基数树。
9.1.1 一层基数树
一层基数树采用的是直接映射的方法
32位机器下才可以用一层基数树,64位机器下不可以,因为2^62次方太大了,早已超出了我们机器的内存的大小了,所以64位机器要用两层基数树或者三层基数树。

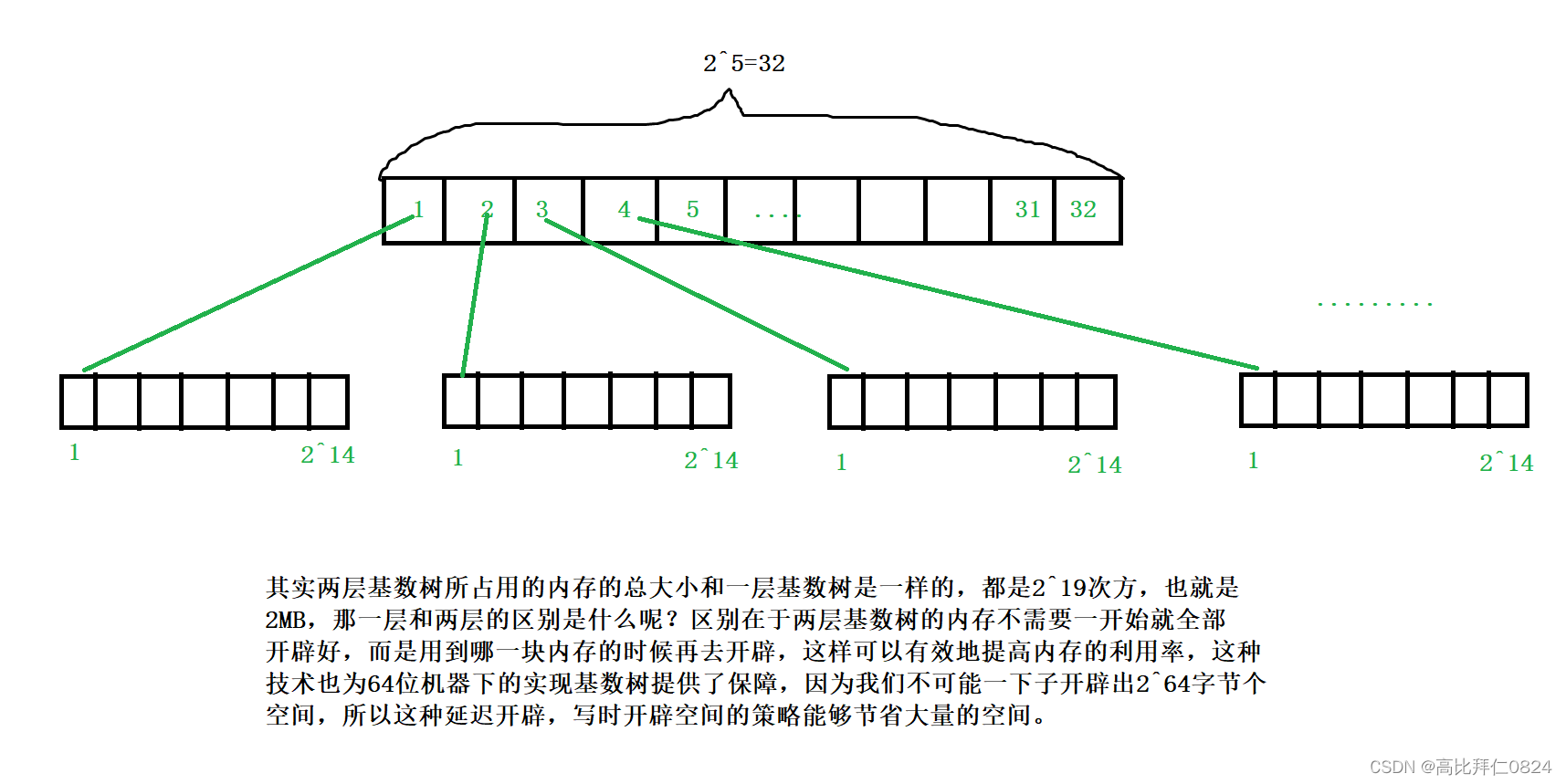
9.1.2 两层基数树
两层基数树是把哈希映射的关系分成两层,第一层是利用低19位的高5位判断该id在第一层的哪一个位置,再按照低14位判断在第二层的哪个位置。
三层基数树也是按照两层基数树的模式继续延伸下去即可,在这也就不过多叙述了,详情可以看后面的代码实现。
9.2 tcmalloc中基数树的源码实现
//基数树,用来代替 idSpanMap,访问时可以不用加锁
// Single-level array
template <size_t BITS>
class TCMalloc_PageMap1 {
private:
static const int LENGTH = 1 << BITS;
void** array_;
public:
typedef uintptr_t Number;
//explicit TCMalloc_PageMap1(void* (*allocator)(size_t)) {
explicit TCMalloc_PageMap1() {
//array_ = reinterpret_cast<void**>((*allocator)(sizeof(void*) << BITS));
size_t size = sizeof(void*) << BITS;
size_t alignSize = SizeClass::_RoundUp(size, 1 << PAGE_SHIFT);
array_ = (void**)SystemAlloc(alignSize >> PAGE_SHIFT);
memset(array_, 0, sizeof(void*) << BITS);
}
// Return the current value for KEY. Returns NULL if not yet set,
// or if k is out of range.
void* get(Number k) const {
if ((k >> BITS) > 0) {
return NULL;
}
return array_[k];
}
// REQUIRES "k" is in range "[0,2^BITS-1]".
// REQUIRES "k" has been ensured before.
//
// Sets the value 'v' for key 'k'.
void set(Number k, void* v) {
array_[k] = v;
}
};
// Two-level radix tree
template <int BITS>
class TCMalloc_PageMap2 {
private:
// Put 32 entries in the root and (2^BITS)/32 entries in each leaf.
static const int ROOT_BITS = 5;
static const int ROOT_LENGTH = 1 << ROOT_BITS;
static const int LEAF_BITS = BITS - ROOT_BITS;
static const int LEAF_LENGTH = 1 << LEAF_BITS;
// Leaf node
struct Leaf {
void* values[LEAF_LENGTH];
};
Leaf* root_[ROOT_LENGTH]; // Pointers to 32 child nodes
void* (*allocator_)(size_t); // Memory allocator
public:
typedef uintptr_t Number;
//explicit TCMalloc_PageMap2(void* (*allocator)(size_t)) {
explicit TCMalloc_PageMap2() {
//allocator_ = allocator;
memset(root_, 0, sizeof(root_));
PreallocateMoreMemory();
}
void* get(Number k) const {
const Number i1 = k >> LEAF_BITS;
const Number i2 = k & (LEAF_LENGTH - 1);
if ((k >> BITS) > 0 || root_[i1] == NULL) {
return NULL;
}
return root_[i1]->values[i2];
}
void set(Number k, void* v) {
const Number i1 = k >> LEAF_BITS;
const Number i2 = k & (LEAF_LENGTH - 1);
ASSERT(i1 < ROOT_LENGTH);
root_[i1]->values[i2] = v;
}
bool Ensure(Number start, size_t n) {
for (Number key = start; key <= start + n - 1;) {
const Number i1 = key >> LEAF_BITS;
// Check for overflow
if (i1 >= ROOT_LENGTH)
return false;
// Make 2nd level node if necessary
if (root_[i1] == NULL) {
//Leaf* leaf = reinterpret_cast<Leaf*>((*allocator_)(sizeof(Leaf)));
//if (leaf == NULL) return false;
static ObjectPool<Leaf> leafPool;
Leaf* leaf = (Leaf*)leafPool.New();
memset(leaf, 0, sizeof(*leaf));
root_[i1] = leaf;
}
// Advance key past whatever is covered by this leaf node
key = ((key >> LEAF_BITS) + 1) << LEAF_BITS;
}
return true;
}
void PreallocateMoreMemory() {
// Allocate enough to keep track of all possible pages
Ensure(0, 1 << BITS);
}
};
// Three-level radix tree
template <int BITS>
class TCMalloc_PageMap3 {
private:
// How many bits should we consume at each interior level
static const int INTERIOR_BITS = (BITS + 2) / 3; // Round-up
static const int INTERIOR_LENGTH = 1 << INTERIOR_BITS;
// How many bits should we consume at leaf level
static const int LEAF_BITS = BITS - 2 * INTERIOR_BITS;
static const int LEAF_LENGTH = 1 << LEAF_BITS;
// Interior node
struct Node {
Node* ptrs[INTERIOR_LENGTH];
};
// Leaf node
struct Leaf {
void* values[LEAF_LENGTH];
};
Node* root_; // Root of radix tree
void* (*allocator_)(size_t); // Memory allocator
Node* NewNode() {
Node* result = reinterpret_cast<Node*>((*allocator_)(sizeof(Node)));
if (result != NULL) {
memset(result, 0, sizeof(*result));
}
return result;
}
public:
typedef uintptr_t Number;
explicit TCMalloc_PageMap3(void* (*allocator)(size_t)) {
allocator_ = allocator;
root_ = NewNode();
}
void* get(Number k) const {
const Number i1 = k >> (LEAF_BITS + INTERIOR_BITS);
const Number i2 = (k >> LEAF_BITS) & (INTERIOR_LENGTH - 1);
const Number i3 = k & (LEAF_LENGTH - 1);
if ((k >> BITS) > 0 ||
root_->ptrs[i1] == NULL || root_->ptrs[i1]->ptrs[i2] == NULL) {
return NULL;
}
return reinterpret_cast<Leaf*>(root_->ptrs[i1]->ptrs[i2])->values[i3];
}
void set(Number k, void* v) {
ASSERT(k >> BITS == 0);
const Number i1 = k >> (LEAF_BITS + INTERIOR_BITS);
const Number i2 = (k >> LEAF_BITS) & (INTERIOR_LENGTH - 1);
const Number i3 = k & (LEAF_LENGTH - 1);
reinterpret_cast<Leaf*>(root_->ptrs[i1]->ptrs[i2])->values[i3] = v;
}
bool Ensure(Number start, size_t n) {
for (Number key = start; key <= start + n - 1;) {
const Number i1 = key >> (LEAF_BITS + INTERIOR_BITS);
const Number i2 = (key >> LEAF_BITS) & (INTERIOR_LENGTH - 1);
// Check for overflow
if (i1 >= INTERIOR_LENGTH || i2 >= INTERIOR_LENGTH)
return false;
// Make 2nd level node if necessary
if (root_->ptrs[i1] == NULL) {
Node* n = NewNode();
if (n == NULL) return false;
root_->ptrs[i1] = n;
}
// Make leaf node if necessary
if (root_->ptrs[i1]->ptrs[i2] == NULL) {
Leaf* leaf = reinterpret_cast<Leaf*>((*allocator_)(sizeof(Leaf)));
if (leaf == NULL) return false;
memset(leaf, 0, sizeof(*leaf));
root_->ptrs[i1]->ptrs[i2] = reinterpret_cast<Node*>(leaf);
}
// Advance key past whatever is covered by this leaf node
key = ((key >> LEAF_BITS) + 1) << LEAF_BITS;
}
return true;
}
void PreallocateMoreMemory() {
}
};
由于上面的基数树是更改idSpanMap的结构的,所以需要把idSpanMap的访问操作修改成对应的基数树的set和get
idSpanMap主要是在PageCache中使用,修改后如下:
PageCache PageCache::_sInst;
//k代表的是这个span的大小k页
Span* PageCache::NewSpan(size_t k)
{
assert(k > 0);
//如果申请的span的大小大于128页,则需要直接向堆申请
if (k > NPAGES - 1)
{
//向堆申请k页内存
void* ptr = SystemAlloc(k);
Span* kSpan = _spanPool.New();
//地址转化成页号
kSpan->_pageId = (PAGE_ID)ptr >> PAGE_SHIFT;
kSpan->_n = k;
//把页号和Kspan的映射关系放进Map中
//_idSpanMap[kSpan->_pageId] = kSpan;
_idSpanMap.set(kSpan->_pageId, kSpan);
return kSpan;
}
else
{
//如果PageCache第k个位置的哈希桶上有k页大小的span,则直接返回一个span
if (!_spanLists[k].Empty())
{
Span* kSpan = _spanLists[k].PopFront();
//把kSpan的页号和对应的Span*的映射关系存放到哈希桶中去,方便
//CentralCache回收小块内存时,查找对应的span
//kSpan代表的是一个k页大小的Span的大块内存,kSpan->_pageId
//代表这个大块内存的起始地址,有k页,所以这k页映射到的都是这个Span
for (PAGE_ID i = 0; i < kSpan->_n; i++)
{
//_idSpanMap[kSpan->_pageId + i] = kSpan;
_idSpanMap.set(kSpan->_pageId + i, kSpan);
}
return kSpan;
}
//走到这里说明PageCache第k个位置的哈希桶没有k页大小的span,则需要遍历
//后面的大于k页的哈希桶,找到了一个n页大小的span就把这个span切分成一个
// k页大小的span和一个n-k页大小的span,k页的返回,n-k页的挂到对应的哈希桶中
//遍历后面的哈希桶
for (size_t i = k + 1; i < NPAGES; i++)
{
//找到了一个不为空的i页的哈希桶,就对它进行切分
if (!_spanLists[i].Empty())
{
//k页的span
Span* kSpan = _spanPool.New();
//n页的span
Span* nSpan = _spanLists[i].PopFront();
//开始把一个n页的span切分成一个k页的span和一个n-k页的span
//
//从nSpan的头上切k页给kSpan,所以kSpan的页号就是nSpan的页号
kSpan->_pageId = nSpan->_pageId;
kSpan->_n = k;//kSpan的页数是k
//被切分以后nSpan的页号需要+=k页,因为头nSpan的头k页已经切分给了kSpan
nSpan->_pageId += k;
nSpan->_n -= k;//nSpan的页数要-=k页,因为nSpan被切走了k页
//把kSpan的页号和对应的Span*的映射关系存放到哈希桶中去,方便
// CentralCache回收小块内存时,查找对应的span
//kSpan代表的是一个k页大小的Span的大块内存,kSpan->_pageId
//代表这个大块内存的起始地址,有k页,所以这k页映射到的都是这个Span
for (PAGE_ID i = 0; i < kSpan->_n; i++)
{
//_idSpanMap[kSpan->_pageId + i] = kSpan;
_idSpanMap.set(kSpan->_pageId + i, kSpan);
}
//nSpan被切分后的首页和尾页的页号和nspan的映射关系也需要保存起来
//以便后续合并,因为合并的方式是前后页合并,往前找肯定找到的是一个span的
//最后一页,往后找一定找的是一个span的第一页,所以挂在PageCache对应哈希桶
//的span的第一页和最后一页与span的关系也需要保存起来
//
//_idSpanMap[nSpan->_pageId] = nSpan;
//_idSpanMap[nSpan->_pageId + nSpan->_n - 1] = nSpan;
_idSpanMap.set(nSpan->_pageId, nSpan);
_idSpanMap.set(nSpan->_pageId + nSpan->_n - 1, nSpan);
if (nSpan->_pageId == 0)
{
int x = 0;
}
//把剩余的n-k页的span头插到对应下标的哈希桶中
_spanLists[nSpan->_n].PushFront(nSpan);
return kSpan;
}
}
//走到这里说明前面的NPAGES个哈希桶中都没有Span,(例如第一次申请内存时)
//则需要向堆申请一个128页大小的span大块内存,挂到对应的哈希桶中
void* ptr = SystemAlloc(NPAGES - 1);
Span* bigSpan = _spanPool.New();
bigSpan->_pageId = (PAGE_ID)ptr >> PAGE_SHIFT;//内存的地址需要转换成页号映射到对应的哈希桶中
bigSpan->_n = NPAGES - 1;
//把NPAGES-1页大小的span头插到对应NPAGES-1号桶中去
_spanLists[bigSpan->_n].PushFront(bigSpan);
//本质是运用了复用的设计,避免代码中出现重复的逻辑
return NewSpan(k);
}
}
Span* PageCache::MapObjectToSpan(void* obj)
{
//计算出obj对应的页号
PAGE_ID id = (PAGE_ID)obj >> PAGE_SHIFT;
访问_idSpanMap的时候需要加锁,避免线程安全的问题
这里使用C++11的RAII锁,出了这个函数这把锁会自动解掉
//std::unique_lock<std::mutex> lock(_pageMtx);
通过页号查找该内存块对应的是哪一个span
//auto ret = _idSpanMap.find(id);
//if (ret != _idSpanMap.end())
//{
// return ret->second;
//}
//else
//{
// assert(false);
// return nullptr;
//}
//换成了基数树作为map存放页号和Span*的映射关系之后,访问的时候是不需要再加锁的,原因有以下几点:
//1、只有在NewSpan函数和ReleaseSpanToPageCache函数会去写基数树。
//2、基数树在写之前就会开好空间,写的过程中是不会影响到基数树的结构的,也就是说在两个线程在访问
// 不同位置时互相是不会受到影响的。
//3、基数树对同一个位置的读写是分离的,线程1对一个位置进行读写的时候,线程2不可能也在对同一个位置进行读写
//写是在申请span和释放span的时候,是在没人用的时候做的;而读是在有人用这个span的时候做的,所以读写是分离的
// 4、另一方面就是NewSpan函数和ReleaseSpanToPageCache函数在调用之前本身就已经加锁了,所以这里就不用加锁了
//但是为什么用stl下的map要加锁呢?本质是红黑树在插入的时候会改变树的结构,一个线程在插入节点改变红黑树的结构,
//一个线程在遍历就会有线程安全的问题,而基数树插入的时候不会影响结构,而且基数树读取的时候并不是遍历,而是直接通过下标
//就访问到了对应的位置的
//通过页号查找该内存块对应的是哪一个span
void* ret = _idSpanMap.get(id);
if (ret != nullptr)
{
return (Span*)ret;
}
else
{
assert(false);
return nullptr;
}
}
//CentralCache把span还回来给PageCache
void PageCache::ReleaseSpanToPageCache(Span* span)
{
//如果span的页数大于128页,则说明这个span是从堆上直接申请的,
//直接释放给堆即可,不能挂到PageCache的哈希桶中,因为PageCache一个只有128个桶
if (span->_n > NPAGES - 1)
{
void* ptr = (void*)(span->_pageId << PAGE_SHIFT);
SystemFree(ptr);
_spanPool.Delete(span);
return;
}
while (1)
{
//找前一页的span,看是否能够和当前页合并,如果能,则循环向前合并,直到不能合并为止
PAGE_ID prevId = span->_pageId - 1;
void* ret = _idSpanMap.get(prevId);
//_idSpanMap中没找到前一页和对应span,说明前一页的内存没有被申请,结束合并
if (ret == nullptr)
{
break;
}
Span* prevSpan = (Span*)ret;
//如果前一页对应的span在CentralCache中正在被使用,结束合并
if (prevSpan->_isUse == true)
{
break;
}
//如果和前一页合并之后会超过哈希桶的最大的映射返回,结束合并
if (prevSpan->_n + span->_n > NPAGES - 1)
{
break;
}
//合并span和prevSpan
span->_pageId = prevSpan->_pageId;
span->_n = prevSpan->_n + span->_n;
//合并之后需要把prevSpan在对应的哈希桶中删除掉
_spanLists[prevSpan->_n].Erase(prevSpan);
//因为prevSpan已经被合并到了span中,所以prevSpan对应的内存可以delete掉了
_spanPool.Delete(prevSpan);
}
while (1)
{
//找span的下一个span的起始页号
PAGE_ID nextId = span->_pageId + span->_n;
void* ret = _idSpanMap.get(nextId);
if (ret == nullptr)
{
break;
}
Span* nextSpan = (Span*)ret;
if (nextSpan->_isUse == true)
{
break;
}
if (nextSpan->_n + span->_n > NPAGES - 1)//曾经写成NPAGES+1了
{
break;
}
//span的起始页号不变,页数相加
span->_n = span->_n + nextSpan->_n;
//合并之后需要把prevSpan在对应的哈希桶中删除掉
_spanLists[nextSpan->_n].Erase(nextSpan);
_spanPool.Delete(nextSpan);
}
//合并得到的新的span需要挂到对应页数的哈希桶中
_spanLists[span->_n].PushFront(span);
//在PageCache中的span要设置为false,好让后面相邻的span来合并
span->_isUse = false;
//为了方便后续的合并,需要把span的起始页号和尾页号和span建立映射关系
//_idSpanMap[span->_pageId] = span;
//_idSpanMap[span->_pageId + span->_n - 1] = span;
_idSpanMap.set(span->_pageId, span);
_idSpanMap.set(span->_pageId + span->_n - 1, span);
}
代码中用的是一层基数树:

9.3 为什么使用基数树在访问时不需要加锁?

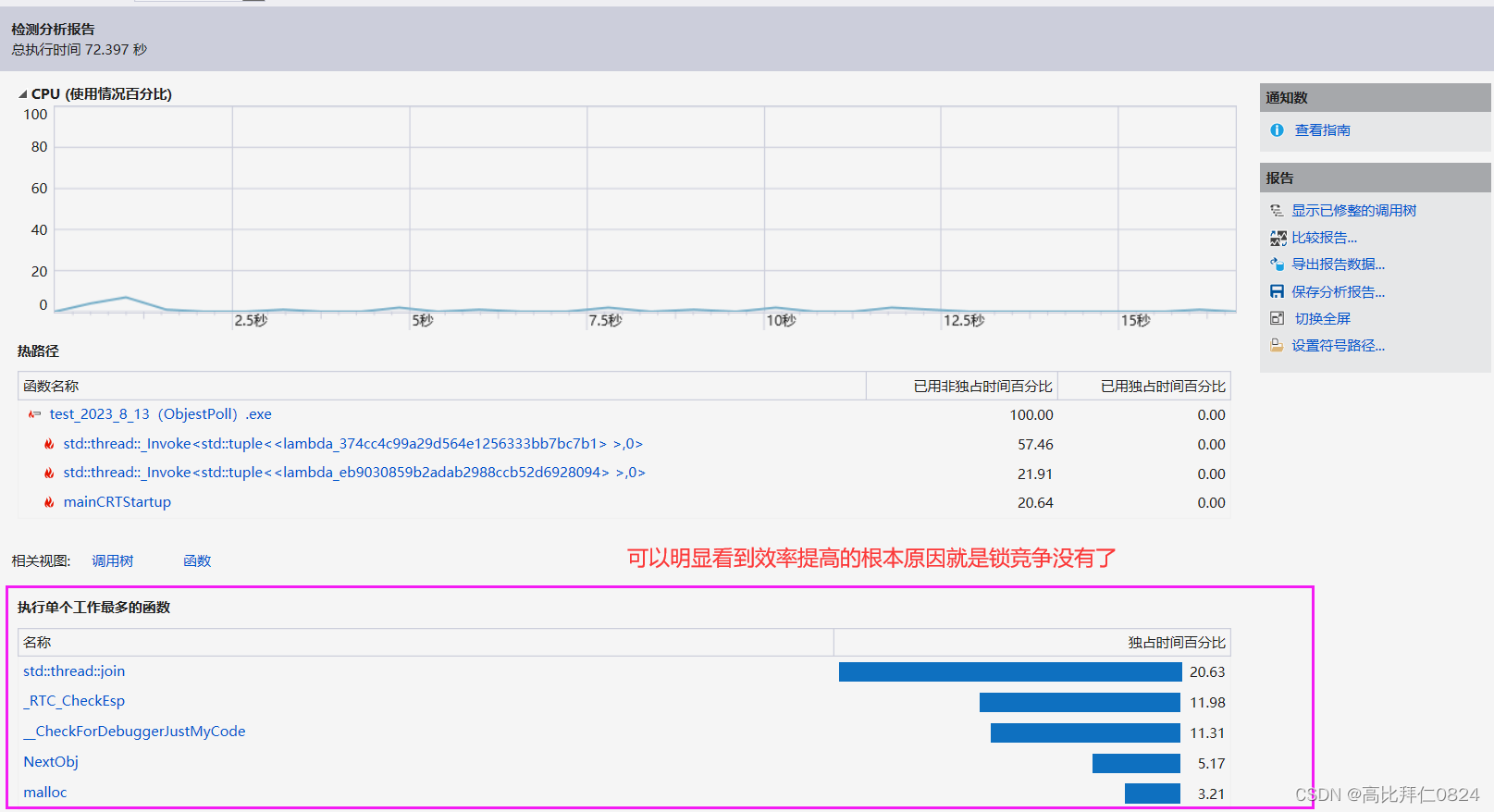
十、使用基数树前后性能对比
使用基数树优化前:我们的内存池比malloc还要稍微慢一些。

使用基数树优化后:我们的内存池的效率大概是malloc的10倍左右的样子,可见,基数树优化后的效率还是提高了不少的。