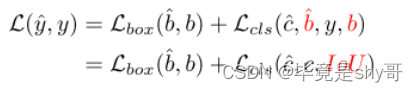Problem - D - Codeforces

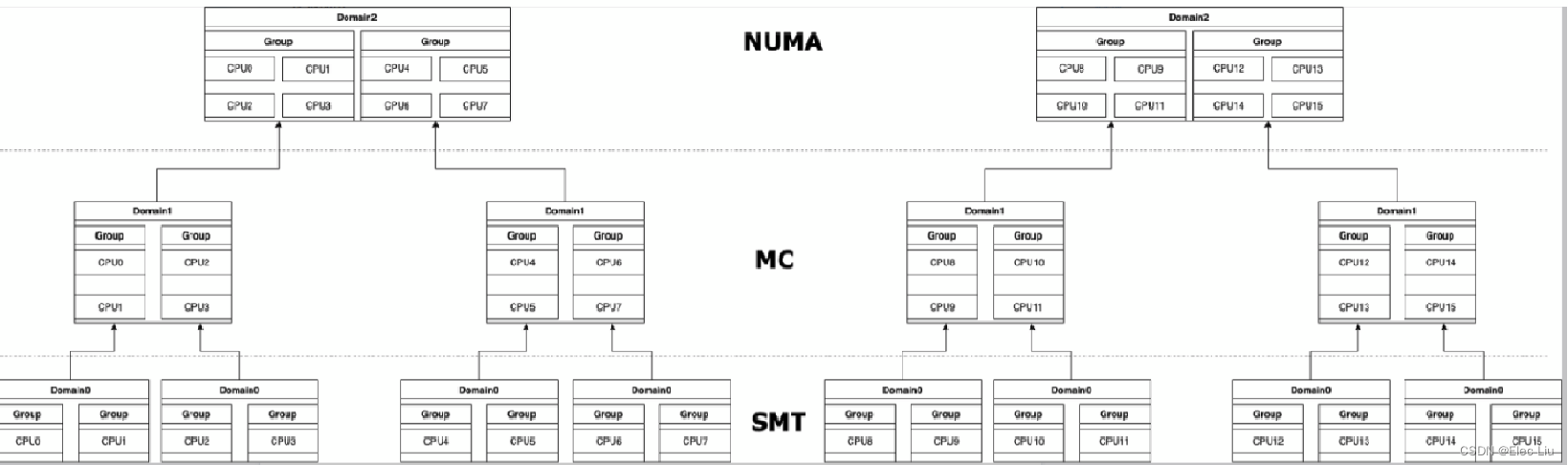
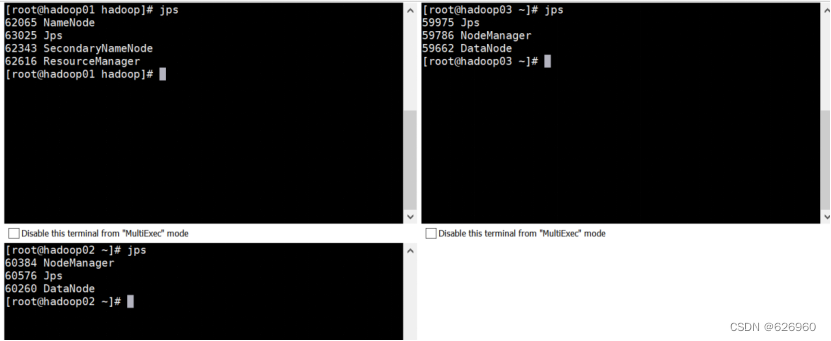
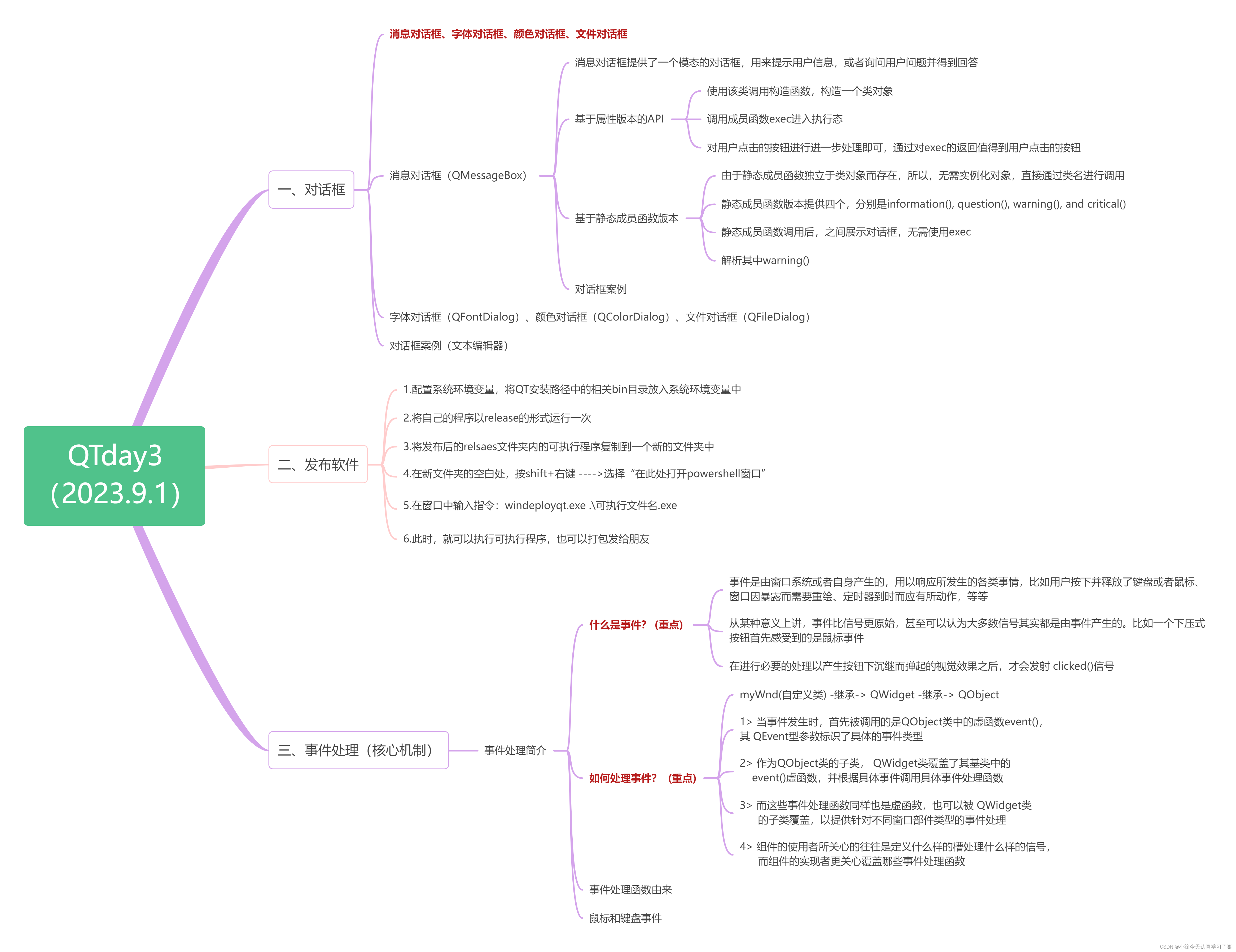
题意：

思路：

首先观察样例可知，我们可以把连续的非0序列看作一个连通块，次数能够最少是因为同一个连通块的可以一次性染色

又观察到，一个连通块，有2和没2也是不一样的

如果有2，那么连通块两端可以和0结合，如果没有2，可以选其中一端和0结合

贪心地从有2的连通块开始染色，再从普通连通块染色，然后剩下的的单独染即可

因为维护了左边第一个0和右边第一个0，注意要判一下边界

Code：

#include <bits/stdc++.h>

#define int long long

using i64 = long long;

constexpr int N = 2e5 + 10;
constexpr int M = 2e5 + 10;
constexpr int P = 2600;
constexpr i64 Inf = 1e18;
constexpr int mod = 1e9 + 7;
constexpr double eps = 1e-6;

int n;
int a[N];
int f[N], vis[N];
int pre[N], suf[N];

int find(int x) {
    return f[x] = (x == f[x]) ? x : find(f[x]);
}
void join(int u, int v) {
    int f1 = find(u), f2 = find(v);
    if (f1 != f2) {
        f[f1] = f2;
    }
}
void solve() {
    std::cin >> n;

    std::vector<int> V, V1;
    for (int i = 1; i <= n; i ++) {
        std::cin >> a[i];
        if (a[i] == 2) V.push_back(i);
        if (a[i] == 1) V1.push_back(i);
    }

    pre[0] = 0;
    suf[n + 1] = n + 1;
    for (int i = 1; i <= n; i ++) {
        if (a[i] == 0) pre[i] = i;
        else pre[i] = pre[i - 1];
    }

    for (int i = n; i >= 1; i --) {
        if (a[i] == 0) suf[i] = i;
        else suf[i] = suf[i + 1];
    }

    for (int i = 1; i <= n; i ++) {
        f[i] = i;
    }

    int l = 1, r = 1;
    while(1) {
        if (l > n || r > n) break;
        while(l <= n && a[l] == 0) l ++;
        r = l;
        while(r <= n && a[r] != 0) {
            r ++;
            if (a[r] != 0 && r - 1 >= 1) {
                join(r, r - 1);
            }
        }
        l = r;
    }

    for (auto x : V) {
        if (!vis[find(x)]) {
            vis[find(x)] = 1;
            if (pre[x] >= 1 && !vis[find(pre[x])]) {
                vis[find(pre[x])] = 1;
                join(x, pre[x]);
            }
            if (suf[x] <= n && !vis[find(suf[x])]) {
                vis[find(suf[x])] = 1;
                join(x, suf[x]);
            } 
        }
    }

    for (auto i : V1) {
        if (!vis[find(i)]) {
            vis[find(i)] = 1;
            bool ok = false;
            if (!vis[find(pre[i])] && pre[i] >= 1) {
                ok = true;
                vis[find(pre[i])] = 1;
                join(i, pre[i]);
            }
            if (!ok) {
                if (!vis[find(suf[i])] && suf[i] <= n) {
                    ok = true;
                    vis[find(suf[i])] = 1;
                    join(i, suf[i]);
                }
            }
        }
    }

    int ans = 0;
    for (int i = 1; i <= n; i ++) {
        if (find(i) == i) ans ++;
    }

    std::cout << ans << "\n";
}
signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    
    int t = 1;

    while (t--) {
        solve();
    }
    
    return 0;
}