文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州
▲ 本章节目的
⚪ 了解Spark的梯度下降法;
⚪ 了解Spark的梯度下降法家族(BGD,SGD,MBGD);
⚪ 掌握Spark的MLlib实现SGD;
一、梯度下降法概念
1. 概述
求解机器学习算法的模型参数,即无约束优化问题时,梯度下降法是最常采用的方法之一,另一种常用的方法是最小二乘法。这里对梯度下降法做简要介绍。
最小二乘法法适用于模型方程存在解析解的情况。如果说一个函数不存在解析解,是不能用最小二乘法的,此时,只能通过数值解(迭代式的)去逼近真实解。

上面的方程就不存在解析解,每个系数无法用变量表达式表达。
梯度下降法要比最小二乘法的适用性更强。
2. 什么是梯度
在微积分里面,对多元函数的参数求∂偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度。
比如函数f(x,y), 分别对x,y求偏导数,求得的梯度向量就是(∂f/∂x, ∂f/∂y)T,简称grad f(x,y)或者▽f(x,y)。
![]()
![]()
对于在点(x0,y0)的具体梯度向量就是(∂f/∂x0, ∂f/∂y0)T.或者▽f(x0,y0),如果是3个参数的向量梯度,就是(∂f/∂x, ∂f/∂y,∂f/∂z)T,以此类推。
3. 这个梯度向量求出来有什么意义
他的意义从几何意义上讲,就是函数变化最快的地方。
具体来说,对于函数f(x,y),在点(x0,y0),沿着梯度向量的方向就是(∂f/∂x0, ∂f/∂y0)T的方向是f(x,y)增加最快的地方。或者说,沿着梯度向量的方向,更加容易找到函数的最大值。
反过来说,沿着梯度向量相反的方向,也就是 -(∂f/∂x0, ∂f/∂y0)T的方向,梯度减少最快,也就是更加容易找到函数的最小值。
二、梯度下降法与梯度上升法
在机器学习算法中,在求最小化损失函数时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数,和模型参数值。
反过来,如果我们需要求解损失函数的最大值,这时就需要用梯度上升法来迭代了。
三、梯度下降法的直观解释
首先来看看梯度下降的一个直观的解释。比如我们在一座大山上的某处位置,由于我们不知道怎么下山,于是决定走一步算一步,也就是在每走到一个位置的时候,求解当前位置的梯度,沿着梯度的负方向,也就是当前最陡峭的位置向下走一步,然后继续求解当前位置梯度,向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步向谷底走下去。
从上面的解释可以看出,梯度下降不一定能够找到全局的最优解,有可能是一个局部最优解。当然,如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解。
四、梯度下降法的相关概念
1. 步长:步长决定了在梯度下降迭代的过程中,每一步沿梯度负方向前进的长度。用上面下山的例子,步长就是在当前这一步所在位置沿着最陡峭最易下山的位置走的那一步的长度。
一般步长的选择:0.1~0.05。步长过小,迭代次数可能过多,收敛速度慢。步长过大,可能会错过最优解,围绕最优解震荡而不收敛。
2. 特征:指的是样本中输入部分,比如样本(x0,y0),(x1,y1),则样本特征为x,样本输出为y。
3. 假设函数:在监督学习中,为了拟合输入样本,而使用的假设函数,比如一个线性函数:
![]()
4. 损失函数:为了评估模型拟合的好坏,通常用损失函数来度量拟合的程度。损失函数极小化,意味着拟合程度最好,对应的模型参数即为最优参数。在线性回归中,损失函数通常为样本输出和假设函数的差取平方:
![]()
为了后续的求导运算方便,一般会乘以1/2
![]()
五、梯度下降法原理
1. 原理概述
1. 先决条件:确认优化模型的假设函数和损失函数;
2. 算法相关参数初始化:主要是初始化参数,算法终止距离以及步长。在没有任何先验知识的时候,可以将所有的参数初始化为0,将步长初始化为1.在调优时再优化;
2. 算法过程
1. 随机选择一个θ(θ1,θ2,……)的初始位置,
2. 用步长乘以损失函数的梯度,得到当前位置下降的距离,并更新下降后的θ
3. 多次迭代第二步,直至收敛于损失函数的极值
4. 得到极值点对应的θ解
![]()
3. 损失函数梯度的推导
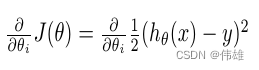
![]()
![]()
![]()
4. θi的更新表达式
![]()
上述θi的更新表达式是在只有一个样本的情况下,我们接下来推广到更一般的情况,比如有n个样本:
![]()
即当前点的梯度方向是由所有的样本决定的。
六、梯度下降法的算法参数
1. 算法的步长选择。在前面的算法描述中,提到取步长为1,但是实际上取值取决于数据样本,可以多取一些值,从大到小,分别运行算法,看看迭代效果,如果损失函数在变小,说明取值有效。
步长太大,会导致迭代过快,甚至有可能错过最优解。步长太小,迭代速度太慢,很长时间算法都不能结束。所以算法的步长需要多次运行后才能得到一个较为优的值。
2. 算法参数的初始值选择。初始值不同,获得的最小值也有可能不同,因此梯度下降求得的只是局部最小值;当然如果损失函数是凸函数则一定是最优解。由于有局部最优解的风险,需要多次用不同初始值运行算法,关键损失函数的最小值,选择损失函数最小化的初值。
3. 归一化。由于样本不同特征的取值范围不一样,可能导致迭代很慢,为了减少特征取值的影响,可以对特征数据归一化。
七、梯度下降法家族(BGD,SGD,MBGD)
1. 批量梯度下降法(Batch Gradient Descent)
批量梯度下降法,是梯度下降法最常用的形式,具体做法也就是在更新参数时使用所有的样本来进行更新。
2. 随机梯度下降法(Stochastic Gradient Descent)
随机梯度下降法,和批量梯度下降法原理类似,区别在与求梯度时没有用所有的n个样本的数据,而是仅仅选取一个样本j来求梯度。
3. BGD和SGD对比
批量梯度下降法和随机梯度下降法是两个极端,一个采用所有数据来梯度下降,一个用一个样本来梯度下降。自然各自的优缺点都非常突出。
1. 对于训练速度来说,随机梯度下降法由于每次仅仅采用一个样本来迭代,训练速度很快,而批量梯度下降法在样本量很大的时候,训练速度不能让人满意。
2. 对于准确度来说,随机梯度下降法由于仅仅用一个样本决定梯度方向,导致解很有可能不是最优。
3. 对于收敛速度来说,由于随机梯度下降法一次迭代一个样本,导致迭代方向变化很大,不能很快的收敛到局部最优解。批量梯度下降法 > 随机梯度下降法。
批量梯度下降法由于采用所有样本计算,所以收敛速度很快,即迭代很少次数就能够收敛到局部或全局最优解。
随机梯度是每次选取一个样本计算,所以收敛速度相比于批量来说就慢很多。
举个例子1:比如批量法10次迭代后收敛,随机法则可能需要100次迭代。
但在海量数据下,使用批量法就不适合了。
举个例子2:因为数据量巨大,批量法可能迭代1次就需要20分钟,而随机法迭代一次只需要1ms
所以总的耗时:批量法=10*20*60*1000ms 随机法=100*1ms。
4. MBGD小批量梯度下降法
结合了以上两种算法,应用没有随机梯度用的多。
对于迭代类型的算法,除了梯度下降法以外,还有牛顿法。
八、案例——MLlib实现SGD
1. 说明
首先需要数据准备工作。MLlib中,线性回归的基本数据是严格按照数据格式进行设置。
数据如下:
1,0 1
2,0 2
3,0 3
5,1 4
7,6 1
9,4 5
6,3 3
第一列是因变量,第二列和第三列是自变量
其次是对既定的MLlib回归算法中数据格式的要求,我们可以从回归算法的源码来分析,源码代码段如下:
def train(
input: RDD[LabeledPoint],
numIterations: Int,
stepSize: Double): LinearRegressionModel = {
train(input, numIterations, stepSize, 1.0)
}
从上面代码段可以看到,整理的训练数据集需要输入一个LabeledPoint格式的数据,因此在读取来自数据集中的数据时,需要将其转化为既定的格式。
从中可以看到,程序首先对读取的数据集进行分片处理,根据逗号将其分解为因变量与自变量,即线性回归中的y和x值。其后将其转换为LabeledPoint格式的数据,这里part(0)和part(1)分别代表数据分开的y和x值,并根据需要将x值转化成一个向量数组。
其次是训练模型的数据要求。numIterations是整体模型的迭代次数,理论上迭代的次数越多则模型的拟合程度越高,但是随之而来的是迭代需要的时间越长。而stepSize是随机梯度下降算法中的步进系数,代表每次迭代过程中模型的整体修正程度。
2. 代码示例
代码示例:
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.regression.{LabeledPoint,LinearRegressionWithSGD}
import org.apache.spark.{SparkConf,SparkContext}
object Demo13{
val conf=new SparkConf().setMaster("local").setAppName("LinearRegression")
val sc=new SparkContext(conf)
def main(args:Array[String]):Unit={
val data=sc.textFile("d://testSGD.txt")
//转换成SGD要求的格式
val parsedData=data.map{line=>
val parts=line.split(",")
LabeledPoint(parts(0).toDouble,Vectors.dense(parts(1).split("").map(_.toDouble)))
}.cache()
//建立模型
val model=LinearRegressionWithSGD.train(parsedData,100,0.1)
//根据测试集检验模型
val prediction=model.predict(parsedData.map((_.features)))
prediction.foreach(println)//查看检验的结果
println("预测数据:x1=0,x2=1时y的取值"+model.predict(Vectors.dense(0,1)))
}
}
打印的结果:
1.0042991995986885
2.008598399197377
3.012897598796066
5.012535240851979
6.976329854342036
9.00284976782234
5.99891292616774
测数据:x1=0,x2=1时 y的取值1.0042991995986885。