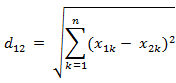背景：

最近大模型输入上文长度增长技术点的研究很火。为何要增长token长度,为何大家如此热衷于增长输入token的长度呢？其实你如果是大模型比价频繁的使用者，这个问题应该不难回答。增长了输入token的长度，那需要多次出入才能得到最终解，得到多个结果需要自己拼接得到最好答案的问题，可以变成一把梭哈直接输出结果。因为上下文长度不够导致对话时候忘记前面讲什么问题、因为背景知识不够需要向量知识库补上下文数据问题、因为允许输入上下文限制导致只能生成代码片段不能生成项目代码，上面这些畏难而退都会因为可输入上下文的增长得到一定程度缓解。
是否可能训练时候短输入推理时候长输入呢？如果解决外推性可以在一定扩展长度范围内可行。外推性是指大模型在训练时和预测时的输入长度不一致，导致模型的泛化能力下降的问题。例如，如果一个模型在训练时只使用了 512 个 token 的文本，那么在预测时如果输入超过 512 个 token，模型可能无法正确处理。这就限制了大模型在处理长文本或多轮对话等任务时的效果。

直觉角度如何解：

1.模型抽局部特征+全局特征融合，局部特征抽取能力强，增加长度无非就是增加特征，全局特征融合能力强可以把增长特征较好融合
2.模型全局视野很宽，在训练时候只用了部分视野；实际推理时候可以把全部视野全用上，来达到比训练时token长能力
3.模型有超宽的分辨率范围，可以根据长度来调整分辨率范围，输入token变长可以自动调整模型分辨率让模型达到最优的视野关注力
4.token有规律，长度的增加信息特征是有简单章法可循（必须随着长度线性增长），那么token增长只需要做一次信息转换就解决信息偏差问题
5.token之间关联性较弱可以近似无关联，那么我们就可以分布的求每部分的信息，然后把每部分特征concat就好了

从数学角度看问题：

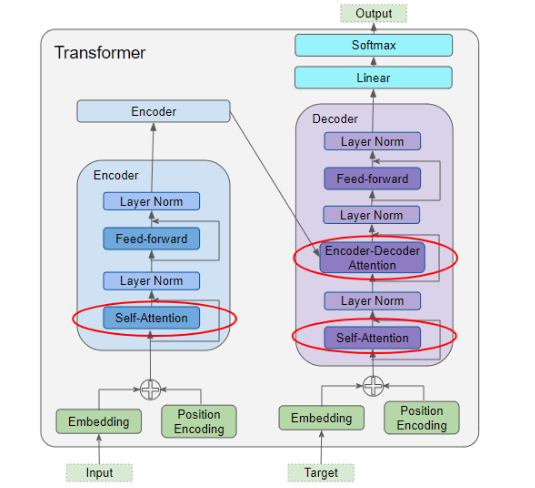
transformer原理简介

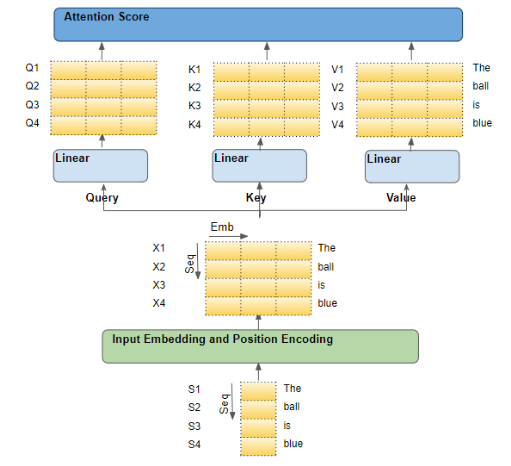
可以把transformer看成是对信息的特征抽取、匹配、赋权的一个过程。输入的embbeding信息经过query算子对信息压缩抽取特征把需要信息变成查询高纬语义（可理解为是对输入信息做了simihash或者lhs），输入embbeding信息经过key算子处理把信息做表征（相当于是把特征入库变成信息唯一key表示），赋权相当于是计算key和query之间特征相似权重。这其实就是一个信息检索过程建模，query算子、key算子、赋权算子全部是需要求解的参数，也就是说transformer相当于是对检索这个流程进行建模，而不是我们一般检索过程流程确定只是求解每个部件参数。所以transformer其实学习到的是如何对信息进行构建query、key表征、赋权；还有一个很巧妙的地方在于tranformer是self信息处理，这样就保证了学习过程可以无需人工标注一堆数据。但是为什么self自信息学习可以让transformer学习到信息query、表征、赋权这一套信息流程，能够外推到任何的信息处理流程。这里面其实有做一个假设：1.信息的近场效应 2.建模的是信息抽取过程，query、key、赋权算子是会经历任何数据，并且算子是有记忆型；所以学习是self自信息但是适用任何没见过信息和非对称输入信息处理。
上面表述估计还是不够清晰,但抓住重点就是transformer之所以能够行知有效，根本在于这个架构看似简单但其实是对信息处理过程建模。模型学习的是通用信息处理过程的流程步骤，把信息抽取的各模块参数、流程一并的建模了；求解过程就是对整个系统的调优求解。所以trnasformer看似简单但是威力巨大。

位置编码说起

但是信息往往是一个序列，也就是说在一段信息之间是有时空关系的。前一段的信息会对后一段的信息有影响，越靠近自己的信息可能对自己影响越大，离得越远的信息对自己影响越小。那么该如何用数学方法来表示这种特性呢，可以分两块来看：
1.如何在序列上表示重要性值,这个其实学过信号处理的同学应该都知道怎么做，无非就是三角函数、傅立叶函数生成波形就好
2.如何随着距离远近做重要性衰减，这学过信号处理的同学也很清楚怎么做，就是搞一个衰减载波函数和波函数相乘就行
序列上表示信号示例：

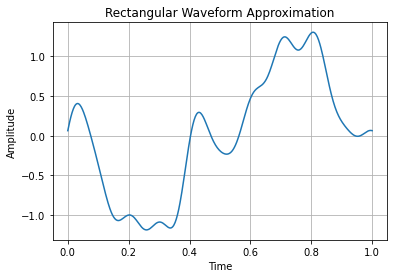
import matplotlib.pyplot as plt
import numpy as np

frequency = 1  # Frequency of the rectangular waveform
amplitude = 1  # Amplitude of the rectangular waveform
duty_cycle = 0.5  # Duty cycle of the rectangular waveform (50% for a symmetric waveform)

t = np.linspace(0, 1, 500)  # Time array
waveform =  amplitude *(np.sin(2 * np.pi * frequency * (-t)) + 
                        1/3 * np.sin(6 * np.pi * frequency * t) +
                        1/5 * np.sin(10 * np.pi * frequency * t)+
                        1/7 * np.sin(11 * np.pi * frequency * t)+
                        1/9 * np.sin(15 * np.pi * frequency * t)+
                        1/13 * np.sin(20 * np.pi * frequency * t))

plt.plot(t, waveform)
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.title('Rectangular Waveform Approximation')
plt.grid(True)
plt.show()

信号衰减函数示例：

import numpy as np
import matplotlib.pyplot as plt

# 生成时间序列
t = np.linspace(0, 10, 1000)

# 生成信号震荡衰减函数（例如，正弦函数衰减）
frequency = 3  # 频率
amplitude = 0.3 # 振幅
decay_rate = 0.6  # 衰减率
signal = amplitude  *(np.sin(2 * np.pi * frequency*t *np.log( decay_rate*t))+frequency)* np.exp( -decay_rate *t)

# 绘制图形
plt.figure(figsize=(10, 6))
plt.plot(t, signal, label='signal')
plt.xlabel('time')
plt.ylabel('amplitude')
plt.title('signal')
plt.legend()
plt.grid(True)
plt.show()

现在有了表示信息序列值的方法，接下来的事就是如何把这个信息和序列表示关联起来，让信息的表征具备序列特性而不是和序列无关的。最直接想到的方法就是把信息的向量表示矩阵和序列算子点乘就行了。然而transformer的实现时候有点违反直觉，他们选了位置embbeding和信息embbeding用concat方式来融合。位置embbeding他们选择了用三角函数Sinusoidal位置编码来实现。

KaTeX parse error: {equation} can be used only in display mode.
其中pk,2i,pk,2i+1分别是位置k的编码向量的第2i,2i+1个分量，d是位置向量的维度。
为什么transformer这么设计也能够起到考量信号序列差异的作用的，我们可以参考苏神这篇文章Transformer升级之路：1、Sinusoidal位置编码追根溯源 - 科学空间|Scientific Spaces来看。
把序列差异建模为以下数学描述：
输入：xm,xn分别表示第m,n个输入，不失一般性，设f是标量函数。像Transformer这样的纯Attention模型，它是全对称的，即对于任意的m,n都有
KaTeX parse error: {equation} can be used only in display mode.
这就是我们说Transformer无法识别位置的原因——全对称性，简单来说就是函数天然满足恒等式f(x,y)=f(y,x)，以至于我们无法从结果上区分输入是[x,y]还是[y,x]。
要打破这种对称性，比如在每个位置上都加上一个不同的编码向量：
KaTeX parse error: {equation} can be used only in display mode.
只要每个位置的编码向量不同，那么这种全对称性就被打破了，即可以用f̃ 代替f来处理有序的输入。
只考虑m,n这两个位置上的位置编码，将它视为扰动项，泰勒展开到二阶：
KaTeX parse error: {equation} can be used only in display mode.
可以看到，第1项跟位置无关，第2到5项都只依赖于单一位置，所以它们是纯粹的绝对位置信息，第6项是第一个同时包含pm,pn的交互项，我们将它记为${\mathbf{p}}_m^{\top }\mathcal{H}{\mathbf{p}}_n$，希望它能表达一定的相对位置信息。
假设$\mathcal{H}=\mathbf{I}$是单位矩阵，此时${\mathbf{p}}_m^{\top }\mathcal{H}{\mathbf{p}}_n={\mathbf{p}}_m^{\top }{\mathbf{p}}_n=⟨{\mathbf{p}}_m,{\mathbf{p}}_n⟩$是两个位置编码的内积，我们希望在这个简单的例子中该项表达的是相对位置信息，即存在某个函数g使得
KaTeX parse error: {equation} can be used only in display mode.
这里的pm,pn是d维向量，这里我们从最简单d=2入手。
对于2维向量，我们借助复数来推导，即将向量[x,y]视为复数x+yi，根据复数乘法的运算法则，得到：
KaTeX parse error: {equation} can be used only in display mode.
为了满足式(5)(5)，我们可以假设存在复数qm−n使得
KaTeX parse error: {equation} can be used only in display mode.
这样两边取实部就得到了式(5)(5)。为了求解这个方程，我们可以使用复数的指数形式，即设
${\mathbf{p}}_m=r_m{e}^{\text{i}{\varphi }_m},{\mathbf{p}}_n^{\ast }=r_n{e}^{-\text{i}{\varphi }_n},{\mathbf{q}}_{m-n}=R_{m-n}{e}^{\text{i}{\Phi }_{m-n}}$带入上式的到：
KaTeX parse error: {equation} can be used only in display mode.
接下来就是求解上面的行列式，求出${\varphi }_m$得到Pm的位置embbeding表示。
对于第一个方程，代入n=m得r2m=R0，即rm是一个常数，简单起见这里设为1就好；对于第二个方程，代入n=0得${\varphi }_m-{\varphi }_0={\Phi }_m$简单起见设ϕ0=0，那么ϕm=Φm，即${\varphi }_m-{\varphi }_n={\varphi }_{m-n}$代入n=m−1得ϕm−ϕm−1=ϕ1那么{ϕm}只是一个等差数列，通解为mθ，因此我们就得到二维情形下位置编码的解为，
KaTeX parse error: {equation} can be used only in display mode.
内积满足线性叠加性，所以更高维的偶数维位置编码，我们可以表示为多个二维位置编码的组合：
KaTeX parse error: {equation} can be used only in display mode.
到这边似乎已经把transformer实现为什么是(1）式的谜团解决了，然而我们稍微动动脑子可能就会想到用sin、cos周期性的三角函数来表示位置特征序列不同位置重要性表示是可以解决，但是距离不同远近值衰减问题似乎是没有解决的；当然你可以讲现在位置embbding表示只是给了一个基底表示，实际上的序列值是多少、远近衰减性还是需要经过模型学习后和模型参数共同作用体现的。理是这个理，但是我们有没办法在位置embbding时候给一个好的起始条件让模型更容易学习表示呢，transofmers应该是给出解法的，这就是${\theta }_i=10000^{-2i/d}$。
利用高频振荡积分的渐近趋零性特性。将上面内积改为以下形式
KaTeX parse error: {equation} can be used only in display mode.
这样问题就变成了积分${\int }_0^1{e}^{\text{i}(m-n){\theta }_t}dt$的渐近估计问题，这样位置embbeding随着距离远近衰减的特性就具备了。

Hybird Window-Full Attention（HFWA）

讲到这你一定会问我这些和增长token该如何做有什么一毛钱关系呢。看起来似乎确实没什么关系，你要解决的是token变长的问题，我却一直在家过位置编码的事情。但你再想想看增长token模型效果会降低的主要原因是什么？主要不就是因为位置相关性，如果是位置无关，那么理论讲模型只要把增长的信息处理下加到后面特征融合层模型效果下降不会太多。所以这也是为什么在讲token增强强先介绍transformer是如何来处理位置embbding的。

1、预测的时候用到了没训练过的位置编码（不管绝对还是相对）；

2、预测的时候注意力机制所处理的token数量远超训练时的数量。更多的token会导致注意力更加分散（或者说注意力的熵变大），从而导致的训练和预测不一致问题

HWFA的思路就是典型的“模型抽局部特征+全局特征融合”，所以你可以看到他的具体实现方法如下：

1、前面L−1层使用Window为w的“Window Attention+RoPE”，满足约束(w−1)(L−1)+1=αN
，这里N是训练长度，为了兼顾训练效果和外推效果，建议在α≤3/4的前提下选择尽量大的w；
2、第L层使用带logn，因子的Full Attention，但是不使用RoPE。

如果用一句话来总结HWFA的做法就是：够不着对方？拔出你那10米长的弹簧刀。啥意思呢就是模型在训练时候，训练的：局部特征抽取能力很强，并且也能很好的把局部特征整合来做信息处理；训练的时候每个局部特征抽取器都得到充分训练并且做了overlap让模型训练token变得更短；但是在实际推理的时候长token信息拖过来，模型各个局部特征抽取能力火力全开，所以可以在不做训练就拓展token长度。

这边有几个关键点：
1.windows窗口方式抽取特征
2.必须要训练模型对windows抽取特征全局特征融合能力
3.相对位置的编码方式很重要，作者用RoPE（绝对位置做改进实现相对位置编码）

NTK-RoPE

这方法实现思路是，模型的感受野不变通过内插或者外插位置让增长token塞进感受野，有点类似照相机镜头不变通过广角模型（调整焦距）实现增长token能力。然后如果只是用位置向量内插或者外差，那其实模型是需要做微调的，类比相机的话镜头不变但是你必须要调整焦距方式来让照相机可以排出好东西。NTK-RoPE用了一个很巧妙的方式来实现不需要微调就能做到token增长；它的做法是：增长token做位置内存让容量变大，为了避免微调他做了一个进制转化工作。比如把10进制编程16进制，这样就可以在不扩位置编码长度情况下让模型可以处理更长token信息。
更妙的地方在于NTK-RoPE对RoPE没做什么太大改动就能得到就好效果，主要就在认知视角的差异带来token长度扩展。认识视角可以看下面：
位置n的旋转位置编码（RoPE），本质上就是数字n的β进制编码！
10进制的数字n，我们想要求它的β进制表示的（从右往左数）第m位数字，方法是
KaTeX parse error: {equation} can be used only in display mode.
RoPE，它的构造基础是Sinusoidal位置编码，可以改写为
KaTeX parse error: {equation} can be used only in display mode.
$\beta =10000^{2/d}$
模运算，它的最重要特性是周期性，式(13)的cos,sincos,sin是不是刚好也是周期函数？所以，除掉取整函数这个无关紧要的差异外，RoPE（或者说Sinusoidal位置编码）其实就是数字n的β进制编码！
进制转换，就是要扩大k倍表示范围，那么原本的β进制至少要扩大成β(k2/d)进制（式(2)虽然是d维向量，但cos,sincos,sin是成对出现的，所以相当于d/2位β进制表示，因此要开d/2次方而不是d次方），或者等价地原来的底数10000换成10000k这基本上就是NTK-aware Scaled RoPE。跟前面讨论的一样，由于位置编码更依赖于序信息，而进制转换基本不改变序的比较规则，所以NTK-aware Scaled RoPE在不微调的情况下，也能在更长Context上取得不错的效果。
直接外推会将外推压力集中在“高位（m较大）”上，而位置内插则会将“低位（m较小）”的表示变得更加稠密，不利于区分相对距离。而NTK-aware Scaled RoPE其实就是进制转换，它将外推压力平摊到每一位上，并且保持相邻间隔不变，这些特性对明显更倾向于依赖相对位置的LLM来说是非常友好和关键的，所以它可以不微调也能实现一定的效果。
RoPE本质上是一种相对位置编码，相对位置是Toeplitz矩阵的一个特例，它长这个样（由于本文主要关心语言模型，所以右上角部分就没写出来了）
KaTeX parse error: {equation} can be used only in display mode.
上式可以发现，相对位置编码的位置分布是不均衡的！0的出现次数最多、1次之、2再次之，以此类推，即n越大出现次数越少。这就意味着，作为一种β进制编码的RoPE，它的“高位”很可能是训练不充分的，换言之高位的泛化能力很可能不如低位。刚才我们说了，NTK-RoPE将外推压力平摊到每一位上，如果这里的猜测合理的话，那么“平摊”就不是最优的，应该是低位要分摊更多，高位分摊更少，这就苏神在NTK-RoPE之上提出改进思路混合进制。

HFWA+ReRoPE

这个方法对应直觉感知方法：“模型有超宽的分辨率范围，可以根据长度来调整分辨率范围，输入token变长可以自动调整模型分辨率让模型达到最优的视野关注力”。
从语言模型的局域性来考察这些方法。所谓局域性，是指语言模型在推断下一个token时，明显更依赖于邻近的token。直接外推保持了局域性（0附近位置编码不变），效果差是因为引入了超出训练长度的位置编码；位置内插虽然没有外推位置编码，但扰乱了局域性（0附近位置编码被压缩为1/k1），所以不微调效果也不好；而NTK-aware Scaled RoPE通过“高频外推、低频内插”隐含了两者优点，保证了局域性，又没有明显外推位置编码，所以不微调也有不错的效果。
有没有能更直接地结合外推和内插的方法呢？有，我们可以设定一个窗口大小w，在窗口内我们使用大小为1的位置间隔，在窗口外我们使用大小为1/k的位置间隔，整个相对位置矩阵如下
KaTeX parse error: {equation} can be used only in display mode.
在RoPE中实现这样的分块运算会明显增加计算量，这也是该思路会被笔者搁置的主要原因。
怎么理解增加计算量呢？我们知道RoPE是“通过绝对位置实现相对位置”，这样只能得到线性的相对位置，而矩阵是非线性的（或者说分段线性的），要实现它只能算两次Attention矩阵，然后组合起来。具体来说，首先用标准的RoPE计算一次Attention矩阵（Softmax之前）。
ReRoPE是用在Full RoPE Attention上的，就是在推理阶段截断一下相对位置矩阵：
$\left(\begin{array}{ccccccccc}0& & & & & & & & \\ 1& 0& & & & & & & \\ 2& 1& 0& & & & & & \\ \ddots & 2& 1& 0& & & & & \\ \ddots & \ddots & 2& 1& 0& & & & \\ \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & & & \\ L-2& \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & & \\ L-1& L-2& \ddots & \ddots & \ddots & 2& 1& 0& \end{array}\right)\to \left(\begin{array}{ccccccccc}0& & & & & & & & \\ 1& 0& & & & & & & \\ \ddots & 1& 0& & & & & & \\ w-1& \ddots & 1& 0& & & & & \\ w& w-1& \ddots & 1& 0& & & & \\ \ddots & w& \ddots & \ddots & 1& 0& & & \\ \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & & \\ w& \ddots & \ddots & w& w-1& \ddots & 1& 0& \end{array}\right)$
ReRoPE只用在Full RoPE Attention上，HWFA则大部分都是Window RoPE Attention，所以“HWFA+ReRoPE”的方案就呼之欲出了：训练阶段将HWFA原本的Full NoPE Attention换成Full RoPE Attention，然后推理阶段则改为Full ReRoPE Attention。这样一来推理阶段切换ReRoPE带来的额外成本就会变得非常少，而且其他层换为Window Attention带来的收益更加显著。
“HWFA+ReRoPE”还可以弥补原本HWFA的效果损失。此前，为了保证长度外推能力，HWFA的Full Attention要去掉位置编码（即NoPE），同时Window Attention的感受野w̃ 要满足(w̃ −1)(L−1)+1=αN（其中L是层数，N是训练长度，0<α≤10），这些约束限制了模型的表达能力，导致了训练效果变差。而引入ReRoPE之后，Window Attention的感受野可以适当取大一些，Full Attention也可以用RoPE，还可以将它放到中间层而不单是最后一层，甚至也可以多于1层Full Attention。这些变化都可以弥补效果损失，并且得益于ReRoPE，长度外推能力并不会有所下降.
这部分详细可以参考苏神文章：
Transformer升级之路：14、当HWFA遇见ReRoPE - 科学空间|Scientific Spaces

截断基实现token增长

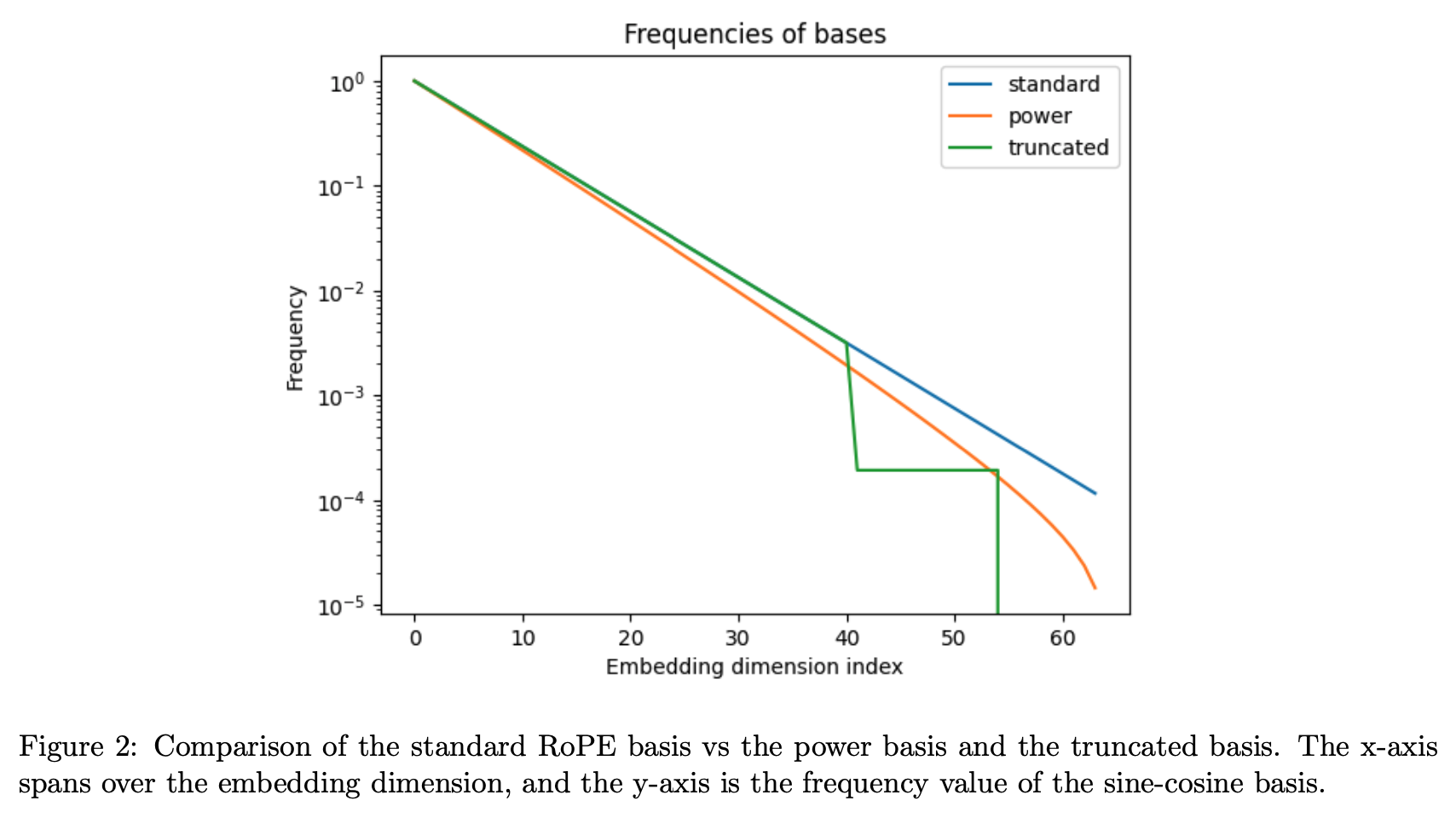
总体来说,截断基是一种新的位置编码方法,目标是通过处理基的频率成分来帮助模型在不看到完整周期性的情况下也能够外推位置。这是一个有潜力的方向,可以与线性缩放等其他方法结合使用。与原始的RoPE基相比,截断基抑制了高频成分,保留了低频成分的周期性,以期望模型可以学习低频位置之间的平滑函数,从而实现更好的上下文长度外推。
原始的RoPE编码依赖所有频率成分来表示距离,高频成分表示短距离,低频成分表示长距离。
截断基保留了低频成分来表示长距离,但屏蔽了高频成分。
在模型见过的上下文长度范围内,由于正弦余弦函数的周期性,模型已经看到了低频成分的全部取值。
这样模型只需要学习低频部分比较简单的周期函数,不需要学习高频部分复杂的周期函数。
这有利于模型外推到更长的未见过的上下文长度。
现有的上下文长度外推技术
线性缩放/位置插值： 在这里，位置向量被一个缩放因子除以。因此，如果原始模型是在位置范围 [0, 1, …, 2048] 上训练的，那么新模型将看到 [0, 1, …, 2048]，其中 x 是缩放因子。

xPos： 我们想要研究是否可以将基本模型的 RoPE 编码方案训练的检查点微调为 xPos [7] 方案。除了要解决整个注意力模块以处理 xPos 独特的键和查询转换的编程障碍外，这种适应方式的主要问题是 xPos 对浮点精度的敏感性。该方法依赖于通过具有大的（绝对）指数的数值来缩放键；这些指数在与查询的点积中稍后取消。然而，对于长上下文，大的值实际上可能会超过 float16 支持的大小。为了解决这个问题，我们选择以 float32 执行核心注意力操作，代价是训练减慢了 2 倍。

随机位置编码: 在这里，我们在范围 [ε, 2] 内均匀地随机化位置值之间的距离，其中 0 < ε ≪ 1，而不是使用典型的 [0, 1, …, n]，其固定间隔为 1。这种方法背后的 intuitions 是，在微调时向模型展示许多不同的位置内部距离，模型将能够在评估时推广到任何细粒度位置的选择，从而通过选择较小的分割来实现上下文长度的有效增加。这与 Ruoss 等人[19]的描述有些相似。我们设置一个上限为 2，以便模型最终将看到一个位置为 n（因为 E[X] ≈ 1，其中 X ∼ U(ε,2)）。我们还设置了一个正的、非零的下限 ε，以避免由于有限数值精度而导致的位置别名问题。
新提出的上下文长度外推技术
Power Scaling： 在原始 RoPE 中，使用的基础如下所示：
Θ = { θ = 1000 0 − 2 ( i − 1 ) ∣ i ∈ { 1 , 2 , . . . , d } } Θ = \{θ = 10000^{-2(i-1)} | i \in \{1,2,..., d\}\} Θ={θ=10000−2(i−1)∣i∈{1,2,...,d}}
其中 d 是嵌入维度。相反，我们使用以下基础：
Θ ∗ = θ i ∗ = θ i 1 − d ∣ i ∈ { 1 , 2 , . . . , 2 } Θ^* = θ_i^* = θ_i^{1-d} | i \in \{1,2,...,2\} Θ∗=θi∗​=θi1−d​∣i∈{1,2,...,2}
其中 k 是一个参数。通过应用这个转换，高频（短距离）元素受到的影响较小，而低频（长距离）元素的频率降低 - 见图表 2。通过这样做，我们希望模型在低频率上执行的外推会较少，因为在训练时它没有看到周期函数的完整范围，从而更好地外推。然而，一个潜在的问题是，模型依赖于跨频率的特定关系，线性变换保留了这些关系，而非线性变换则破坏了这些关系。
Truncated Basis： 从上面方程，我们使用以下基础：

${\theta }_i=\{\begin{array}{ll}\theta & \text{for }\theta \ge b,\\ \rho & \text{for }a<\theta <b,\\ 0& \text{for }\theta \le a.\end{array}$

这里 ρ 是一个相对较小的固定值，a 和 b 是选择的截断值。这里的思想是，我们希望保留基础的高频分量，但将低频元素设置为一个常数值 - 在本例中为 0。通过这样做，通过明智选择的截断 a，模型将在微调时体验到在周期性正弦和余弦函数的情况下基础的所有值，并因此在评估时更好地外推到更大的上下文长度。然而，模型仍然需要能够区分跨越其训练的整个上下文的距离，因此我们还包括固定频率 ρ。总之，我们希望通过这种基础，模型可以避免在整个 RoPE 基础上学习复杂系数的问题，而是通过学习更长距离上的平滑函数来进行外推。
通过这些技术，研究旨在让模型能够更好地在更长的上下文长度下进行外推，从而提高其性能。

小结：

本文对为什么要增长输入token长度做了简要介绍；然后从直觉的角度提出了在训练模型输入长度不变的情况下，可能的几种拓展输入长度的方法；然后回顾了transformers位置编码如何实现；记者回顾进来一些针对训练时输入长度不变，使用时长度变长的解决思路。
直觉的5种解法：
1.模型抽局部特征+全局特征融合，局部特征抽取能力强，增加长度无非就是增加特征，全局特征融合能力强可以把增长特征较好融合
2.模型全局视野很宽，在训练时候只用了部分视野；实际推理时候可以把全部视野全用上，来达到比训练时token长能力
3.模型有超宽的分辨率范围，可以根据长度来调整分辨率范围，输入token变长可以自动调整模型分辨率让模型达到最优的视野关注力
4.token有规律，长度的增加信息特征是有简单章法可循（必须随着长度线性增长），那么token增长只需要做一次信息转换就解决信息偏差问题
5.token之间关联性较弱可以近似无关联，那么我们就可以分布的求每部分的信息，然后把每部分特征concat就好了
进来论文解决方案：HFWA、NTK-RoPE、HFWA+ReRoPE、截断基法。