文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州
▲ 本章节目的
⚪ 掌握Spark的距离度量和相似度度量;
⚪ 掌握Spark的欧氏距离;
⚪ 掌握Spark的曼哈顿距离;
⚪ 掌握Spark的切比雪夫距离;
⚪ 掌握Spark的最小二乘法;
一、距离度量和相似度度量
1. 概念介绍
在数据分析和数据挖掘的过程中,我们经常需要知道个体间差异的大小,进而评价个体的相似性和类别。而如何来度量数据之间的差异则成为关键,分类算法或聚类算法的本质都是基于某种度量(距离度量和相似度度量)来实现的。
2. 距离度量
距离度量(Distance)用于衡量个体在空间上存在的距离,距离越远说明个体间的差异越大。
例如:欧几里得距离(Euclidean Distance)。常见的距离测量方法有如下几个:
1.欧氏距离
2.明可夫斯基距离
3.曼哈顿距离
4.切比雪夫距离
5.马氏距离
3. 相似度度量
1.向量空间余弦相似度(Cosine Similarity)
2.皮尔森相关系数(Pearson Correlation Coefficient)
二、欧氏距离
1. 欧氏距离(Euclidean Distance)
在二维和三维空间中的欧氏距离的就是两点之间的距离。
二维空间的欧氏距离:

二维平面上两点a(x1,y1)与b(x2,y2)间的欧氏距离:
![]()
三维空间两点a(x1,y1,z1)与b(x2,y2,z2)间的欧氏距离:
![]()
两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的欧氏距离:
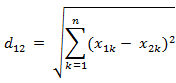
也可以用表示成向量运算的形式&#