在Python编程中,有列表、元组和字典三类变量可以使用,方便数据的存储与处理,而bash中仅有字符串变量、数组、函数可用,方法运用上受到限制,这与bash基于C语言,注重语法结构的严谨有关。而Python等高级语言更侧重于数据的组合与复用,方便处理,也与现代内存增大,价格低廉有关。
本文在介绍python使用的同时,重点讨论用bash编程求水仙花数。
水仙花数指一个三位数:每位数的3次方之和等于这个数。
例如:153是一个水仙花数:153=1^3+5^3+3^3
我们本案例目标:打印输出所有的水仙花数,从小数开始,升序。每行一个。
一、python语言实现
用python语言实现输出水仙花数的功能,十分方便。
首先,设置一个循环变量,一个3位数的整数,从100取值开始,一一验证,每位数的3次方相加与此数相比较,相等为水仙花数(记录、打印),不相等时,变量取值自动加1,再进行验证,如此循环,直到999为止。如此就可以查找并打印出所有的水仙花数。
for循环:
for i in range(100,1000)
python循环取值:开始100,结束1000-1(1000不取值)
对于每一个数,要计算其每位数的3次方之和,有多种方法:
1.先转$i为字符型数据,再对每一位切片,求出其整数之3次方
2.由$i对10求余,求模,得到每一位数,求出其整数之3次方
定义一个变量sum记录每一个数的各位数之3次方之和
1.由求余数计算立方和
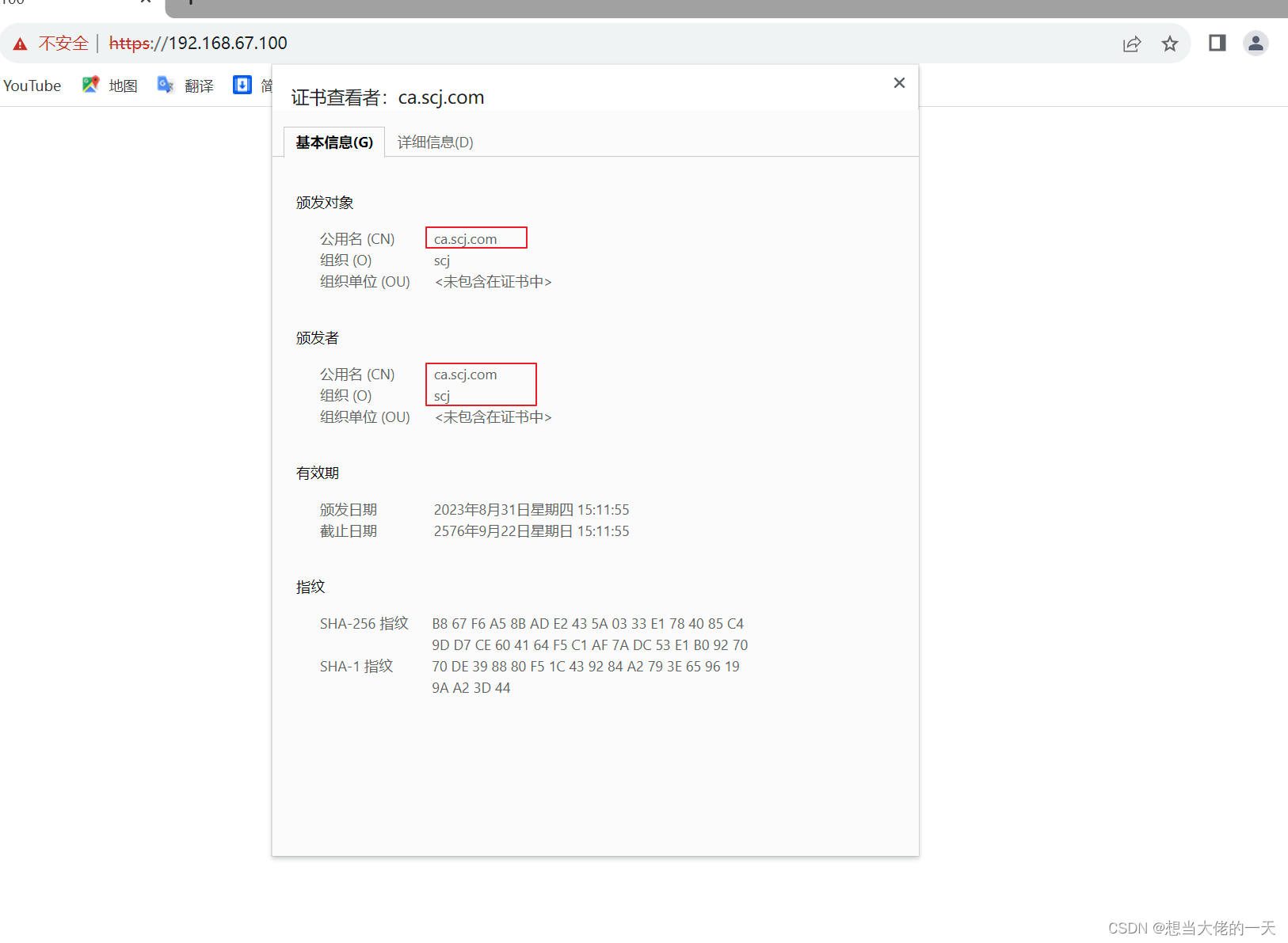
for i in range(100,1000):
sum = int(i%10)**3+int(i/10%10)**3+int(i/100%10)**3
if sum == i:
print(i)
2.由字符切片获得各位数
a.用pow()函数求3次方
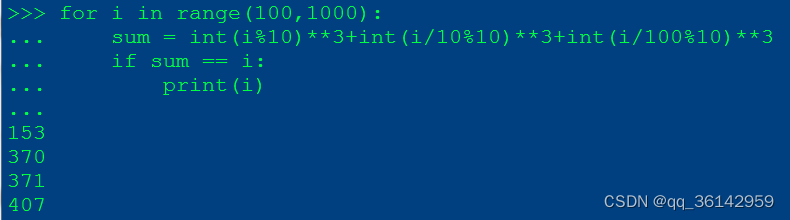
由切片可以获得字符串的各个元素,再转为整型数值,用pow()函数求3次方
for i in range(100,1000):
num = str(i)
hundred = int(num[0]) # 百位数
ten = int(num[1]) # 十位数
one = int(num[2]) # 个位数
if (pow(one,3) + pow(ten,3) + pow(hundred,3)) == i:
print(i)
b.用m**n计算m的n次方
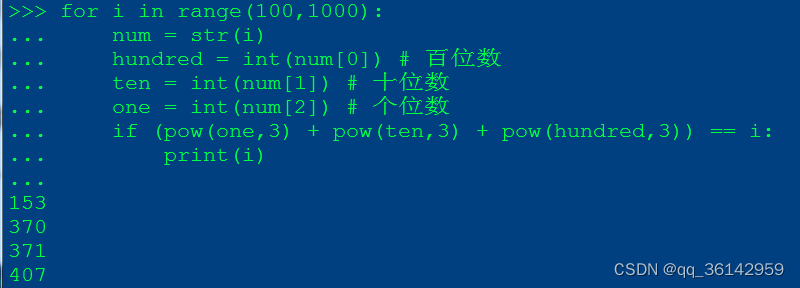
由切片可以获得字符串的各个元素,再转为整型数值,用m**n计算m的n次方
for i in range(100,1000):
num = str(i)
hundred = int(num[0]) # 百位数
ten = int(num[1]) # 十位数
one = int(num[2]) # 个位数
if int(num[0])**3 + int(num[1])**3 + int(num[2])**3 == i:
print(i)
3.由函数达得目标
用定义函数来进行测试。
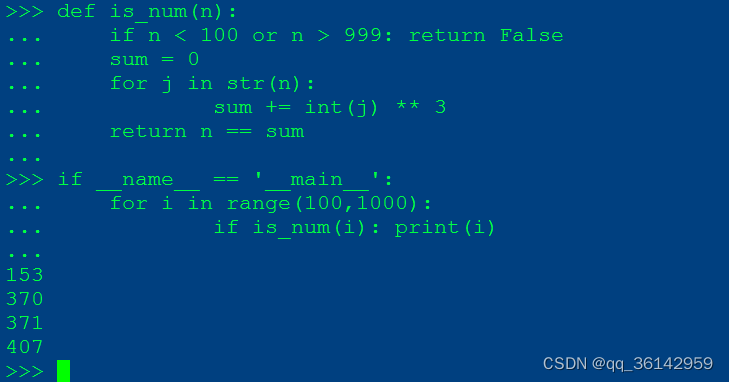
def is_num(n):
if n < 100 or n > 999: return False
sum = 0
for j in str(n):
sum += int(j) ** 3
return n == sum
if __name__ == '__main__':
for i in range(100,1000):
if is_num(i): print(i)
二、bash语言实现
Linux下用bash语言实现输出水仙花数的功能,方法和代码基本上与python相同。
除循环结构写法不太一样,对变量的处理也有稍微差别。思路与方法相同,就可以快速改写,完成目标。
1.多层for循环嵌套
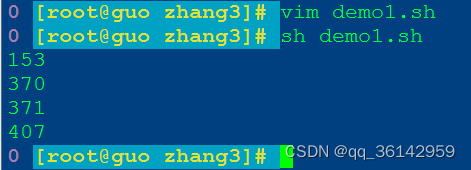
#!/bin/bash
# 求水仙花数
for((i=1;i<10;i++))
do
for((j=0;j<10;j++))
do
for((k=0;k<10;k++))
do
a=$((i**3+j**3+k**3))
b=$((i*100+j*10+k))
if [ $a -eq $b ];then
echo "$a"
fi
done
done
done

把一个三位数,取得每一位数字,这里用了最直观的想法:
取每一位数字,再计算3次方,相加就可以了。
更有效率的方法是:不断地除10取余。
2.while循环求数字的各位数
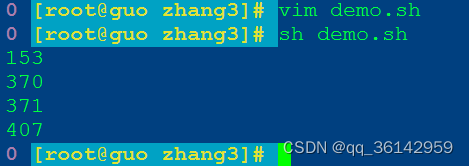
#!/bin/bash
for ((i=100;i<=999;i++))
do
sum=0
n=$i
while [ $n -gt 0 ]
do
m=$((n%10)) # 通过对10求余数,第一次得到个位数
sum=$((sum+m*m*m)) # 每次求出位数的3次方,进行累加
n=$((n/10)) # 个位数处理完后,再把原数对10取整
# 据此,进行第二次循环,第三次循环
done
if [ $sum -eq $i ];then
echo $i
fi
done
题外话
bash代码求月季花数:
取一个四位数,如果它的每个位上的数字的4次方和与自身相等,则可以称之为四季花数。
与3位的水仙花数相同,计算每位数的4次方之和,再验证是否等于这个四位数。
我们修改一下水仙花数求解代码,在命令行执行。写成一行代码,方便快速执行。
for ((i=1000;i<=9999;i++)); do sum=0; n=$i; while [ $n -gt 0 ];do k=$((n%10)); sum=$((sum+k*k*k*k)); n=$((n/10)); done; if [ $sum -eq $i ]; then echo "四季花数是 $i"; fi; done

扩展设想
其实这类问题还可以扩展为更一般的问题:
有一个N位数,如果它的每一位数字的N次方之和等于自身,则称它为N阶的花朵数。
请求出所有的10阶花朵数。
这个问题就要考虑效率了!感兴趣的可以深入探讨。