pytorch中 nn.Conv2d的简单用法

news2024/10/6 2:22:21

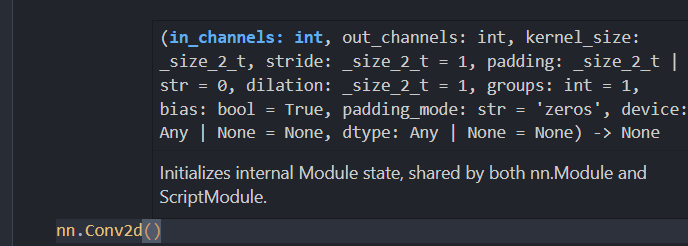
torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True,padding_mode='zeros')

参数介绍：

in_channels：卷积层输入通道数
out_channels：卷积层输出通道数
kernel_size：卷积层的卷积核大小
padding：填充长度
stride：卷积核移动的步长
dilation：是否采用空洞卷积
groups：是否采用分组卷积
bias：是否添加偏置参数
padding_mode：padding的模式

如果输入大小为：数量N即批处理大小（batch size），输入通道数C_in，输入高度H_in，输入宽度C_in。输出大小为：数量N，输出通道数C_out，输出高度H_out，输出宽度C_out。
$\quad (N, C_{in},H_{in},W_{in}) \\ output: \quad (N,C_{out}, H_{out}, W_{out})$
之间的转换为：
$(N_i,C_{out}) = bias(C_{out}) + \sum_{k=0}^{C_{in}-1}weight(C_{out},k) * (N{i},k)$

$H_{out} = [ \frac {H_{in} + 2 * padding[0] - dilation[0] *(kernal_size[0] - 1) - 1}{stride[0]} + 1]$

$W_{out} = [ \frac {W_{in} + 2 * padding[1] - dilation[1] * (kernel_size[1] - 1) - 1} {stride[1]} + 1]$

对于二维简化的：
$W_{in},H_{in} \quad 输入的宽、高 \\ W_{out},H_{out} \quad 输出的宽，高 \\ F \quad 卷积核的大小 \\ S \quad 步长 \\ P \quad 边界填充$
那么输出的宽、高为：
$W_{out} = \frac {W_{in} - F_{W} + 2P} S + 1 \\ H_{out} = \frac {H_{in} - F_{H} + 2P} S + 1$
在pytorch中的使用

直接使用（不常见）

import torch 
import torch.nn as nn 
# https://www.bilibili.com/video/BV1644y1h7LN/?spm_id_from=333.337.search-card.all.click&vd_source=13dfbe5ed2deada83969fafa995ccff6

# 输入通道数
in_channels = 1
# 输出通道数 
out_channels = 1
# 批处理大小 
batch_size = 1
# 卷积核大小 (3,3)
kernel_size = 3
# 输入规格
input_size = [batch_size, in_channels, 4, 4]

# nn.Conv2d使用，其他默认值
conv_layer = torch.nn.Conv2d(in_channels, out_channels, kernel_size)
# 随机输入特征图
input_feature_map = torch.randn(input_size)
# 打印输入特征图形状
print(input_feature_map.shape)
# 求出输出特征图
output_feature_map = conv_layer(input_feature_map)
# 打印出卷积核的规格
print(conv_layer.weight.shape)
# weight == out_channel * in_channel * height * weight
# 打印输出特征图大小
print(output_feature_map.shape)

输出：

torch.Size([1, 1, 4, 4])
torch.Size([1, 1, 3, 3])
torch.Size([1, 1, 2, 2])

封装为类的形式

import torch 
from torch import nn

# 定义一个同样操作的卷积类
class Foo(nn.Module):
    def __init__(self, in_channel, out_channel):
        super(Foo,self).__init__()
        self.layer = nn.Sequential(
            nn.Conv2d(in_channels=in_channel, out_channels=out_channel, kernel_size=3)
        )
    def forward(self, x):
        return self.layer(x)

# 实例化一个
conv2 = Foo(1,1)
# 输出特征图， input_feature_map_2 和 input_feature_map是相同的值
output_feature_map_2 = conv2(input_feature_map_2)
print(output_feature_map_2)

输出：

tensor([[[[ 0.5144,  0.0672],
          [ 0.2169, -0.0591]]]], grad_fn=<ConvolutionBackward0>)

可以观察到，这两个操作相同但是结果值却不相同。这是因为虽然两者实现了相同的卷积操作，但由于它们的初始化和权重值的不同，因此输出结果可能不完全一致。 另外，对于卷积操作的结果，输出的张量形状可能会有所不同，但数值内容应该是相似的。如果希望确保两种方式得到的输出结果完全一致，可以尝试使用相同的初始化参数，并确保权重值相同。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/957348.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！