---

前言

吴恩达 week5

一、归一化输入

1、均值方差归一化

均值方差归一化。
要注意：我们要对训练数据集和测试数据集使用相同的u与方差。
对于测试数据集，我们不能确定测试的数据有什么，必然无法求出其均值方差。
对于测试数据集我们要使用训练数据集的均值和方差。
这样才能使我们的数据在同一分布上。

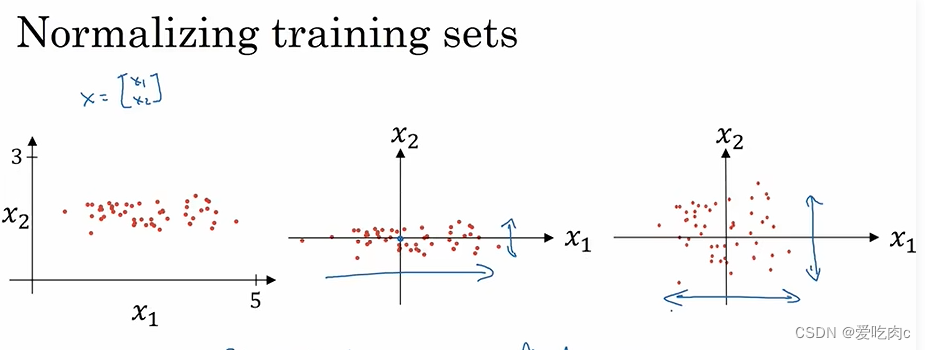
2、why normalize input?

如果我们的数据分布在不同的规模上，比如当我们使用梯度下降取优化J时，
左图：
我们的学习率要设置的小一些，
且也是来回跌宕直到最低点。
右图：
我们的学习率就可以设置的相对大一些。
且不管从哪里开始都可以。也可以避免左右来回跌宕的情况（学习率不是特别大的情况下）。

所以归一化输入也可以提高我们算法的效率

二、梯度消失，爆炸

1.梯度

如果w设置的不合理，可能会导致深度网络中的梯度爆炸或者消失的问题。
若梯度爆炸，则我们无法更好的训练我们的模型。
若梯度消失，则我们每次会走的步数很小，训练的时间太久。

2.深度网络学习初始化

为了防止梯度消失或爆炸，我们就需要更加细致的初始化我们的参数。
如z=w1*x1+…+b
若x太大，则我们就希望w小些。
要求选择Relu作为激活函数，w权值采样于(0,2/n[L-1])分布下，n[L-1]为输入样本个数。
在python中实现：即方差在（0,2/n[L-1])分布下，
np.random.randn(layers_dims[l], layers_dims[l - 1])
2/ np.sqrt(layers_dims[l - 1])
选择tanh作为激活函数，w权值采样于(0,1/n[L-1])分布下，n[L-1]为输入样本个数。
/ np.sqrt(layers_dims[l - 1])
另一种：
2/n[L-1]+n[L]

三、梯度检验

对于反向传播时的梯度，我们使用的是求导的具体值。
为了检验梯度的准确性，我们可以采用数值上近似的方式。
利用求导公式。

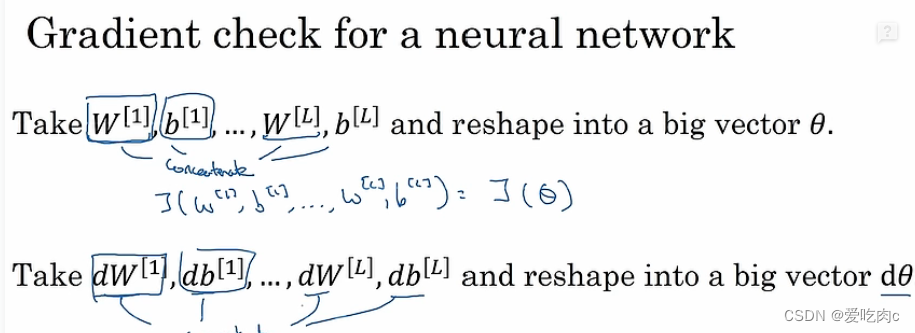
梯度检验

①在写好反向传播公式的时候，你没有办法保证执行反向传播的所有细节全部都是正确的，因此要进行梯度检验，保证反向传播可以正确实施。
②双边误差更准确。即数学中的求导公式

如何确定我们求导的误差没有错误呢？
利用图中的3，对我们求出来的近似值与真实的求导数值进行一个计算
若小于10的-7次方，则我们的反向求导没错。
若在10-5，我们需要检查一下我们写的梯度的近似的代码有没有错误。
若大于10-3 则我们的代码编写有错。

①不要在训练数据时，使用梯度检验，因为梯度检验太耗时，我们应该只在debug时使用。
②如果我们算出来的梯度与实际的梯度差距很大，则我们可以根据我们计算出来的梯度dtheta[i]，看它包含哪个dW，db,以此来确定我们找错的范围。
③不要忘记正则化，更好的计算，更多的使用L2
④在梯度检验时，要关闭dropout，因为dropout的损失函数不确定，无法梯度检验,梯度检验是在J的基础上求的。
⑤在求反向梯度时，我们可能在w,b很小时求得的数据是对的，但是当迭代几次，参数变大之后，梯度可能就不准确了，因此我们可以在初始时检验一次，在迭代几次之后再检验一次。