2023-08-31每日一题

一、题目编号

1761. 一个图中连通三元组的最小度数

二、题目链接

点击跳转到题目位置

三、题目描述

给你一个无向图，整数 n 表示图中节点的数目，edges 数组表示图中的边，其中 edges[i] = [ui, vi] ，表示 ui 和 vi 之间有一条无向边。

一个 连通三元组 指的是三个节点组成的集合且这三个点之间两两有边。

连通三元组的度数 是所有满足此条件的边的数目：一个顶点在这个三元组内，而另一个顶点不在这个三元组内。

请你返回所有连通三元组中度数的 最小值 ，如果图中没有连通三元组，那么返回 -1 。

示例 1：
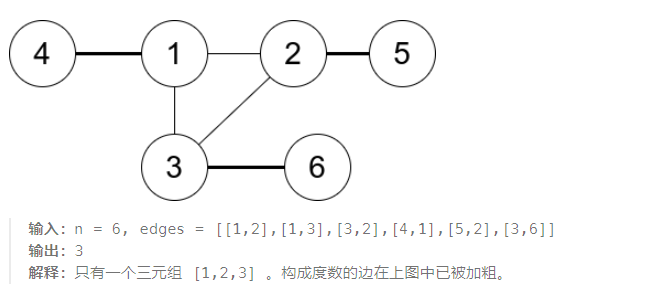
在这里插入图片描述
示例 2：

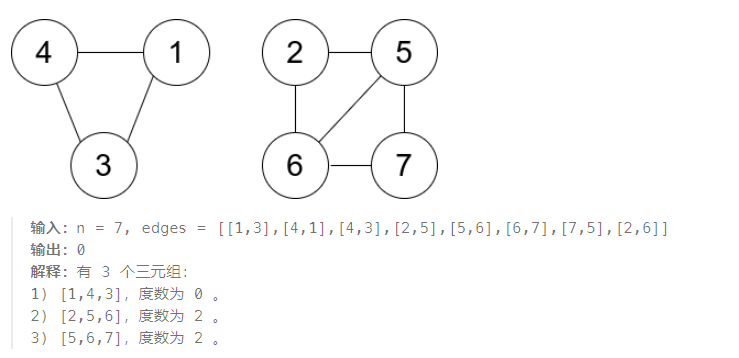
提示：

2 <= n <= 400
edges[i].length == 2
1 <= edges.length <= n * (n-1) / 2
1 <= u_i, v_i <= n
u_i != v_i
图中没有重复的边。

四、解题代码

class Solution {
public:
    int minTrioDegree(int n, vector<vector<int>>& edges) {
        vector<vector<int>> g(n, vector<int>(n));
        vector<int> degree(n);

        for (auto&& edge: edges) {
            int x = edge[0] - 1, y = edge[1] - 1;
            g[x][y] = g[y][x] = 1;
            ++degree[x];
            ++degree[y];
        }
        
        int ans = INT_MAX;
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {
                if (g[i][j] == 1) {
                    for (int k = j + 1; k < n; ++k) {
                        if (g[i][k] == 1 && g[j][k] == 1) {
                            ans = min(ans, degree[i] + degree[j] + degree[k] - 6);
                        }
                    }
                }
            }
        }
        return ans == INT_MAX ? -1 : ans;
    }
};