前两篇暴力递归转动态规划的文章中,都是通过从上到下的一种思路来解决的问题,这篇文章会通过数组从左向右遍历的方式,来将暴力递归转成动态规划。
题目
有两个等长的数组 w[] 和 v[],w[i] 和 v[i] 分别表示 i 号物品的重量和价值,给定一个正整数 bag,表示背包的承重,所装货物不能超过背包的承重,返回你能装下最多的价值是多少?
暴力递归
暴力递归的重点就在于尝试,所尝即所得,首先将暴力递归的方法试出来后,根据暴力递归的方法转成动态规划。
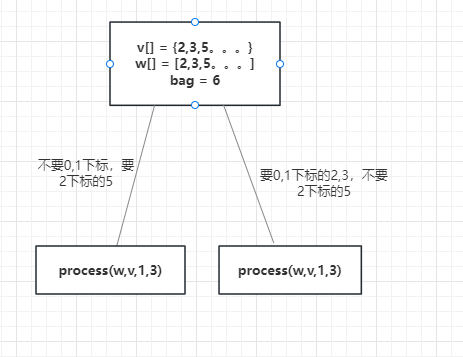
方法的整体思想是这样的,不去管之前货物的拿取情况,从第 index 号货物开始,只关注index 和之后的货物,如果要当前货物, 这用背包重量 - 当前货物重量,并获取当前货物价值,如果不要当前货物,则直接 index 向下走。
代码
主方法调用process,根据前面分析,如果process方法能够根据所传参数返回最大价值,则暴力递归方法就完成了,
public static int maxValue(int[] w, int[] v, int bag) {
//边界判断,如果v w满足以下条件,说明是无用参数,返回0
if (w == null || v == null || w.length != v.length || w.length == 0 || v.length == 0) {
return 0;
}
return process(w, v, bag, 0);
}
接下来完善process方法。
其中,关于bag的边界条件判断中,有一些小坑,比如说注释中部分:
- bag 为什么只能小于 0 ? 因为,如果bag在获取当前货物后,重量刚好为0,下一个货物的weight = 0,但是value巨大,要不要获取? 应该是可以获取的。所以bag < 0。
- bag < 0后,为什么返回 -1 而不是 0 ? 因为,如果我当前货物是最后一个,下一个会走index = v.length,会返回0,但如果此时我超重了,bag < 0 的时候也返回0的话,递归返回给上游的信息是不是还要用当前货物的价值 + 这个0,但此时的货物是不应该装背包的,所以要return -1,并且先调用next看要当前货物的返回值来进行判断。
//不考虑之前的,从index出发,看是否要当前货物
private static int process(int[] w, int[] v, int bag, int index) {
/* if (bag <= 0){
return 0;
}
if (bag < 0){
return 0;
}
int p2 = v[index] + process(w, v, bag - w[index], index + 1);
*/
if (bag < 0) {
return -1;
}
//当前位置来到了数组长度位置,说明没货物了,return 0。
if (index == v.length) {
return 0;
}
//如果不要当前货物,则背包重量无变化,去下一个货物
int p1 = process(w, v, bag, index + 1);
//如果要当前货物,则背包重量 - 货物重量,并且 + 当前货物价值。
int p2 = 0;
//此处需要先判断,当前货物要完后,背包是否超重,所以先获取next的返回值
int next = process(w, v, bag - w[index], index + 1);
if (next != -1) {
p2 = v[index] + next;
}
return Math.max(p1, p2);
}
此时,暴力递归的方法已经完成,来看如果转成动态规划。之前说过,暴力递归转动态规划很重要的一条就是根据可变参数看子过程有没有重复解。这时候举一个实际的例子列出调用过程就能看出来。
代码中,我们的可变参数是bag的剩余和重量和index,从例子中可以看出,有重复解,OK,那我们开始根据暴力递归的代码改动态规划。
动态规划
根据上面的分析,已经找到了可变参数(index【行】以及背包剩余容量【列】)。根据可变参数确定dp缓存表大小,并创建dp缓存表。
并且根据暴力递归代码可以分析出:
- index是可达到数组长度位置。
- 背包剩余容量也是从满的开始,所以数组长度位置也是可到达的。
根据暴力递归base case以及调用关系可以分析出。
- 当 index == v.length return 0,所以dp表最后一行的值都是0。
- 不管是否取当前货物,每次调用process方法都是取index + 1,所以整个依赖过程是前面行依赖后面行,
获取dp表后怎么填充?根据暴力递归改写代码即可!!!所求的值,就是从0开始的背包最大价值,所以获取dp[0][bag]位置数即可。
//根据可变参数,确定dp表范围
//N:可到达N ,所以是0 ~ N +1
//bag: 可到达bag -1 ~ bag + 1
public static int maxValue2(int[] w, int[] v, int bag) {
if (w == null || v == null || w.length != v.length || w.length == 0 || v.length == 0) {
return 0;
}
int N = v.length;
//数组初始化都是0,所以不用对dp表最后的行进行循环赋值操作
int[][] dp = new int[N + 1][bag + 1];
//因为是后面行依赖前面行,所以从最后行开始向前遍历
for (int index = N - 1 ; index >= 0; index--) {
//填充bag剩余容量rest
for (int rest = 0; rest <= bag; rest++) {
int p1 = dp[index +1][rest];
int p2 = 0;
int next = rest - w[index] < 0 ? -1 : dp[index + 1][rest - w[index]];
if (next != -1){
p2 = v[index] + next;
}
dp[index][rest] = Math.max(p1,p2);
}
}
return dp[0][bag];
}