【LeetCode算法系列题解】第6~10题

- LeetCode 6. N 字形变换（中等）
- LeetCode 7. 整数反转（中等）
- LeetCode 8. 字符串转换整数-atoi（中等）
- LeetCode 9. 回文数（简单）
- LeetCode 10. 正则表达式匹配（困难）

LeetCode 6. N 字形变换（中等）

【题目描述】

将一个给定字符串 s 根据给定的行数 numRows，以从上往下、从左到右进行 Z 字形排列。
比如输入字符串为 "PAYPALISHIRING" 行数为 3 时，排列如下：

P   A   H   N
A P L S I I G
Y   I   R

之后，你的输出需要从左往右逐行读取，产生出一个新的字符串，比如："PAHNAPLSIIGYIR"。
请你实现这个将字符串进行指定行数变换的函数：

string convert(string s, int numRows);

【示例1】

输入：s = "PAYPALISHIRING", numRows = 3
输出："PAHNAPLSIIGYIR"

【示例2】

输入：s = "PAYPALISHIRING", numRows = 4
输出："PINALSIGYAHRPI"
解释：
P     I    N
A   L S  I G
Y A   H R
P     I

【示例3】

输入：s = "A", numRows = 1
输出："A"

【提示】

$1\le s.length\le 1000$
$1\le numRows\le 1000$
s 由英文字母（小写和大写）、',' 和 '.' 组成

【分析】

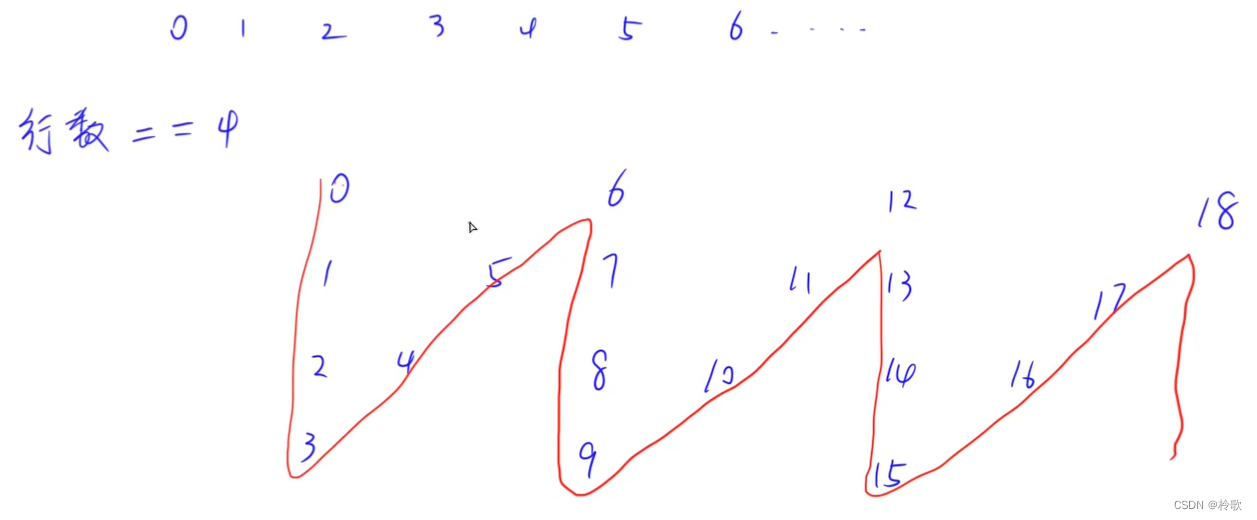
在这里插入图片描述

如上图所示，我们用数字来观察规律，设行数为 $n$ 。

首先看第一行，0到6一共间隔 $2 n - 2$ 个数，因为从0走到3有 $n - 1$ 个数，3走到6也有 $n - 1$ 个数，因此第一行为从0开始的公差为 $2 n - 2$ 的等差数列。同理最后一行为从 $n - 1$ 开始的公差为 $2 n - 2$ 的等差数列。

对于中间行，以第二行为例，由两个等差数列组成，一个是在直线上的数列：1、7、13，这是从1开始的公差为 $2 n - 2$ 的等差数列；还有一个是在斜线上的数列：5、11、17，这是从5（可以看成 $2 n - 2 - i$ ， $i$ 表示这一行的第一个数）开始的公差为 $2 n - 2$ 的等差数列。因此中间行就是先输出第一个等差数列的第一项，然后输出第二个等差数列的第一项，再输出第一个等差数列的第二项，以此类推。

【代码】

class Solution {
public:
    string convert(string s, int n) {
        if (n == 1) return s;  // 特判
        string res;
        for (int i = 0; i < n; i++)
        {
            if (i == 0 || i == n - 1)  // 第一行或最后一行
                for (int j = i; j < s.size(); j += 2 * n - 2)
                    res += s[j];
            else
                // j表示第一个等差数列，k表示第二个等差数列
                for (int j = i, k = 2 * n - 2 - i; j < s.size() || k < s.size(); j += 2 * n - 2, k += 2 * n - 2)
                {
                    if (j < s.size()) res += s[j];
                    if (k < s.size()) res += s[k];
                }
        }
        return res;
    }
};

LeetCode 7. 整数反转（中等）

【题目描述】

给你一个 32 位的有符号整数 x ，返回将 x 中的数字部分反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 $2^{31}, 2^{31} - 1]$ ，就返回 0。
假设环境不允许存储 64 位整数（有符号或无符号）。

【示例1】

输入：x = 123
输出：321

【示例2】

输入：x = -123
输出：-321

【示例3】

输入：x = 120
输出：21

【示例4】

输入：x = 0
输出：0

【提示】

$-2^{31}\le x\le 2^{31} - 1$

【分析】

首先有个小 Tips：C++中负数取模的结果也为负数，如 $-1234\% 10=-4$ 。

直接用 $x\% 10$ 求出 $x$ 的个位数 $a$ ，然后 $res = res * 10 + a$ ，根据负数取模的特性易知该方式同样适用于负数。

注意我们当做无法使用 long long 类型，因此做溢出判断的时候需要对判断公式做一个变换。

【代码】

class Solution {
public:
    int reverse(int x) {
        int res = 0;
        while (x)
        {
            // res * 10 + x % 10 > MAX -> res > (MAX - x % 10) / 10
            if (res > 0 && res > (INT_MAX - x % 10) / 10) return 0;
            if (res < 0 && res < (INT_MIN - x % 10) / 10) return 0;
            res = res * 10 + x % 10;  // x不管正负都通用
            x /= 10;
        }
        return res;
    }
};

LeetCode 8. 字符串转换整数-atoi（中等）

【题目描述】

请你来实现一个 myAtoi(string s) 函数，使其能将字符串转换成一个 32 位有符号整数（类似 C/C++ 中的 atoi 函数）。
函数 myAtoi(string s) 的算法如下：

读入字符串并丢弃无用的前导空格。
检查下一个字符（假设还未到字符串末尾）为正还是负号，读取该字符（如果有）。确定最终结果是负数还是正数。如果两者都不存在，则假定结果为正。
读入下一个字符，直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。
将前面步骤读入的这些数字转换为整数（即，“123” -> 123，“0032” -> 32）。如果没有读入数字，则整数为 0。必要时更改符号（从步骤 2 开始）。
如果整数数超过 32 位有符号整数范围 $2^{31}, 2^{31} - 1]$ ，需要截断这个整数，使其保持在这个范围内。具体来说，小于 $2^{31}$ 的整数应该被固定为 $2^{31}$ ，大于 $2^{31}-1$ 的整数应该被固定为 $2^{31}-1$ 。
返回整数作为最终结果。

注意：

本题中的空白字符只包括空格字符 ' '。
除前导空格或数字后的其余字符串外，请勿忽略任何其他字符。

【示例1】

输入：s = "42"
输出：42

【示例2】

输入：s = "   -42"
输出：-42

【示例3】

输入：s = "4193 with words"
输出：4193

【提示】

$0\le s.length\le 200$
s 由英文字母（大写和小写）、数字（0-9）、' '、'+'、'-' 和 '.' 组成

【分析】

模拟处理字符串即可，判断溢出的方式与上一题相似，唯一的一个坑点是负数的最小值的绝对值是比正数的最大值多1的，因此当恰好等于最小值时 $res$ 存不下对应的正数，因此需要直接返回最小值。

【代码】

class Solution {
public:
    int myAtoi(string s) {
        int idx = 0;
        while (idx < s.size() && s[idx] == ' ') idx++;  // 过滤前导空格
        int op = 1;  // 标记正负，没有正负号时默认为正
        if (s[idx] == '-') op *= -1, idx++;
        else if (s[idx] == '+') idx++;
        int res = 0;
        while (idx < s.size() && s[idx] >= '0' && s[idx] <= '9')
        {
            int x = s[idx] - '0';
            // res * 10 + x > MAX -> res > (MAX - x) / 10
            if (op > 0 && res > (INT_MAX - x) / 10) return INT_MAX;
            // -res * 10 - x < MIN -> -res < (MIN + x) / 10
            if (op < 0 && -res < (INT_MIN + x) / 10) return INT_MIN;
            if (-res * 10 - x == INT_MIN) return INT_MIN;  // 特判刚好等于最小值
            res = res * 10 + x;
            idx++;
        }
        return res * op;
    }
};

LeetCode 9. 回文数（简单）

【题目描述】

给你一个整数 x，如果 x 是一个回文整数，返回 true；否则，返回 false。
回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。
例如，121 是回文，而 123 不是。

【示例1】

输入：x = 121
输出：true

【示例2】

输入：x = -121
输出：false
解释：从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。

【示例3】

输入：x = 10
输出：false
解释：从右向左读, 为 01 。因此它不是一个回文数。

【提示】

$-2^{31}\le x\le 2^{31} - 1$

【分析】

简单题，可以转换成字符串来做，也可以使用数值方法来做，用之前的方法逐步将 $x$ 的个位取出来构建出新的数，然后判断两数是否相等即可。

【代码】

【字符串解法】

class Solution {
public:
    bool isPalindrome(int x) {
        if (x < 0) return false;  // 负数一定不是回文数
        string s = to_string(x);
        return s == string(s.rbegin(), s.rend());
    }
};

【数值解法】

class Solution {
public:
    bool isPalindrome(int x) {
        if (x < 0) return false;  // 负数一定不是回文数
        long long res = 0;  // 1234567899之类的数翻转后会溢出int
        int tmp = x;
        while (tmp) res = res * 10 + tmp % 10, tmp /= 10;
        return res == x;
    }
};

LeetCode 10. 正则表达式匹配（困难）

【题目描述】

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配，是要涵盖整个字符串 s 的，而不是部分字符串。

【示例1】

输入：s = "aa", p = "a"
输出：false
解释："a" 无法匹配 "aa" 整个字符串。

【示例2】

输入：s = "aa", p = "a*"
输出：true
解释：因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

【示例3】

输入：s = "ab", p = ".*"
输出：true
解释：".*" 表示可匹配零个或多个（'*'）任意字符（'.'）

【提示】

$1\le s.length\le 20$
$1\le p.length\le 20$
s 只包含从 a-z 的小写字母
p 只包含从 a-z 的小写字母，以及字符 . 和 *
保证每次出现字符 * 时，前面都匹配到有效的字符

【分析】

这题很难想到是 DP 问题，因此难度不小。我们一步步分析状态表示和状态计算：

状态表示 $f [i] [j]$ ：
- 集合：所有 $s[1\sim i]$ 和 $p[1\sim j]$ （下标从1开始）的匹配方案。
- 属性：bool 类型，表示是否存在一个合法方案。
状态计算：
- $p[j]\ne *$ ，那么直接看 $s [i]$ 和 $p [j]$ 是否匹配即可，若 s[i] == p[j] 或者 p[j] == '.'，且满足 $s$ 的前 $i - 1$ 个字符和 $j$ 的前 $j - 1$ 个字符也匹配，那么 $s [i]$ 和 $p [j]$ 匹配，即可以写出以下状态转移方程：
  f[i][j] = f[i - 1][j - 1] && (s[i] == p[j] || p[j] == '.')
- $p [j] = *$ ，那么我们需要枚举一下 * 表示多少个字符，如果表示0个字符，则 $s$ 的前 $i$ 个字符和 $j$ 的前 $j - 2$ 个字符匹配；如果表示1个字符，则 $s$ 的前 $i - 1$ 个字符和 $j$ 的前 $j - 2$ 个字符匹配，且 s[i] == p[j - 1]；如果表示2个字符，则 $s$ 的前 $i - 2$ 个字符和 $j$ 的前 $j - 2$ 个字符匹配，且 s[i - 1] == p[j - 1] && s[i] == p[j - 1]。因此可以写出以下状态转移方程（没有将 p[j - 1] == '.' 写进去，别忘了这种情况也算匹配）：
  f[i][j] = f[i][j - 2] || (f[i - 1][j - 2] && s[i] == p[j - 1]) || (f[i - 2][j - 2] && s[i - 1] == p[j - 1] && s[i] == p[j - 1]) ...
  现在我们进行优化，写出 f[i - 1][j] 的状态转移方程如下：
  f[i - 1][j] = f[i - 1][j - 2] || (f[i - 2][j - 2] && s[i - 1] == p[j - 1]) ...
  因此可以写出优化后的状态转移方程（将 p[j - 1] == '.' 考虑进去）：
  f[i][j] = f[i][j - 2] || f[i - 1][j] && (s[i] == p[j - 1] || p[j - 1] == '*')

【代码】

class Solution {
public:
    bool isMatch(string s, string p) {
        int n = s.size(), m = p.size();
        s = ' ' + s, p = ' ' + p;  // 在首部加一个空格，因为我们要从第一位开始
        vector<vector<bool>> f(n + 1, vector<bool>(m + 1));
        f[0][0] = true;
        for (int i = 0; i <= n; i++)
            for (int j = 1; j <= m; j++)  // p为空肯定无法匹配，而s为空不一定
            {
                if (i && p[j] != '*')  // 注意i不能为0，因为需要使用f[i - 1]
                    f[i][j] = f[i - 1][j - 1] && (s[i] == p[j] || p[j] == '.');
                else if (p[j] == '*')
                    // 同样注意i不能为0
                    f[i][j] = f[i][j - 2] || i && f[i - 1][j] && (s[i] == p[j - 1] || p[j - 1] == '.');
            }
        return f[n][m];
    }
};