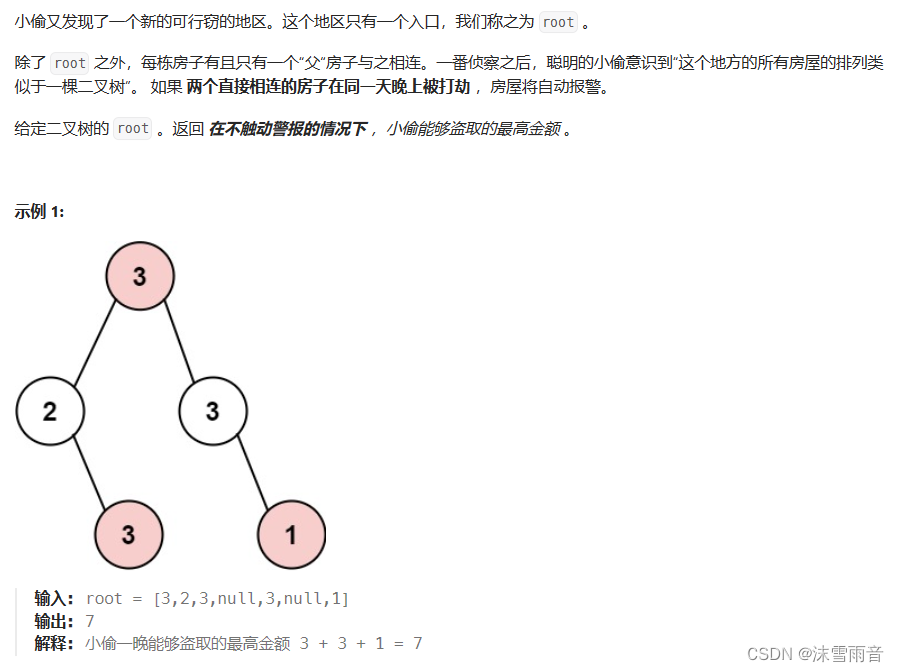
引入思考:
1.微信分销系统中有一个返利,大家应该都知道,比如B是A的下线,C是B的下线,那么在分钱返利的时候A可以分B,C的钱,这时候我们是不是就要分别找B,C的最后上级。这个问题我们一般怎么来解决呢?
2.斐波那契数列: 1 1 2 3 5 8 13 21 有什么特点? 从第三个数开始 就等于前面两个数相加; 数论思想:利用数学公式或者定理或者规律求解问题; f(n) = f(n-1) + f(n-2)
什么是递归?
1.递归的定义: 递归是一个非常重要的算法思想,应用也是相当的广泛,包括我们后面学的数据结构尤其是树形结构里面跟递归是密不可分的。所以大家是一定要学懂它的,其实递归说起来很简单,生活中也是经常可以碰到这个场景。
比如我们在某窗口排队人太多了,我不知道我排在第几个,那么我就问我前面的人排第几个, 因为知道他排第几我就知道我是第几了。但前面的人也不知道自己排第几那怎么办呢?他也可以继续往前面问,直到问到第一个人,然后从第一个人一直传到我这里 我就很清楚的知道我是第几了。以上这个场景就是一个典型的递归。
我们在这个过程中大家有没有发现一个规律那么就是会有一个问的过程,问到第一个后有一个回来的过程吧。这就是递(问)加归(回)。那么这个过程我们是不是可以用一个数学公式来求解呢?那这个数学公式又是什么? f(n)=f(n-1)+1
f(n):表示我的位置
f(n-1):表示我前面的那个人;
自己调用自己;
时间空间复杂度为O(n)
最简单的递归实现
递归,回溯; 递归的关键相信大家已经知道了就是要求出这个递归公式,找到终止条件。现在我们可以回到课堂前跟大家讲的那个斐波那契数列数列: 1 1 2 3 5 8 13
这个的数列我们称之为斐波那契数列
他的求解公式:f(n)=f(n-1)+f(n-2)
终止条件:n<=2 f(n)=1
public class Fibonacci {
// 1 1 2 3 5 8 13
// f(n)=f(n-1)+f(n-2)
public static int fab(int n) { // 分析一段代码好坏,有两个指标,时间复杂度和空间复杂度 都是:O(2^n)
if (n <= 2)
return 1; // 递归的终止条件
return fab(n - 1) + fab(n - 2); // 继续递归的过程
}
}
如下图:每次递归是都是2^n次方,所以时间空间复杂度都是O(2^n)

如何优化递归?
(1)使用非递归。所有的递归代码理论上是一定可以转换成非递归的。简单点就是for循环
(2)加入缓存:把我们中间的运算结果保存起来,这样就可以把递归降至为o(n)
(3)尾递归:什么是尾递归?尾递归就是调用函数一定出现在末尾,没有任何其他的操作了。
因为我们编译器在编译代码时,如果发现函数末尾已经没有操作了,这时候就不会创建新的栈,而且覆盖到前面去。 倒着算,不需要在回溯了,因为我们每次会把中间结果带下去。
package algorithm.rec;
public class Fibonacci {
private static int data[]; // 初始换全部是0
// 1 1 2 3 5 8 13
// f(n)=f(n-1)+f(n-2)
public static int fab(int n) { // 分析一段代码好坏,有两个指标,时间复杂度和空间复杂度 都是:O(2^n)
if (n <= 2)
return 1; // 递归的终止条件
return fab(n - 1) + fab(n - 2); // 继续递归的过程
}
public static int fac(int n) { // 求N的阶乘 用普通递归怎么写 5=5*4*3*2*1=> f(n) =
if (n <= 1)
return 1;
return n * fac(n - 1);
}
public static int noFab(int n) { // 不用递归 O(n)
// 循环
if (n <= 2)
return 1;
int a = 1;
int b = 1;
int c = 0;
for (int i = 3; i <= n; i++) {
c = a + b;
a = b;
b = c;
}
return c;
}
public static int fab2(int n) { // 用数组来做缓存 将为了O(n),空间也降至为O(n)
if (n <= 2)
return 1; // 递归的终止条件
if (data[n] > 0) {
return data[n];
}
int res = fab2(n - 1) + fab2(n - 2); // 继续递归的过程
data[n] = res;
return res;
}
public static int tailfab(int pre,int res,int n) { // 分析一段代码好坏,有两个指标,时间复杂度和空间复杂度 都是: O(n)
if (n <= 2)
return res; // 递归的终止条件
return tailfab(res, pre + res, n - 1); //JDK源码
//参数:
/**
* n 是肯定有的
* res 上一次运算出来结果
* pre 上上一次运算出来的结果
*/
}
public static int tailFac(int n, int res) { // 尾递归 传结果,res就是我们每次保存的结果
System.out.println(n + ":" + res); // 这个地方打印出来的值是怎么样的?
if (n <= 1)
return res;
return tailFac(n - 1, n * res); //倒着算
}
public static void main(String[] args) {
for (int i = 1; i <= 45; i++) {
long start = System.currentTimeMillis();
System.out.println(i + ":" + tailfab(1,1,i) + " 所花费的时间为"
+ (System.currentTimeMillis() - start) + "ms");
}
//tailFac(5, 1);
/*
* for (int i = 1; i <= 45; i++) { long start =
* System.currentTimeMillis(); System.out.println(i + ":" + fab(i) +
* " 所花费的时间为" + (System.currentTimeMillis() - start) + "ms"); }
*/
/*for (int i = 1; i <= 45; i++) {
long start = System.currentTimeMillis();
System.out.println(i + ":" + noFab(i) + " 所花费的时间为"
+ (System.currentTimeMillis() - start) + "ms");
}
System.out.println("==================================");
System.out.println("加了缓存的情况");
for (int i = 1; i <= 45; i++) {
data = new int[46];
long start = System.currentTimeMillis();
System.out.println(i + ":" + fab2(i) + " 所花费的时间为"
+ (System.currentTimeMillis() - start) + "ms");
}*/
}
}