算法随想录刷题60Day

---

目录

前言

打家劫舍1 (数组)

打家劫舍2（环形数组）

打家劫舍3（二叉树）

---

前言

今天主要讨论不相邻选择类问题，会在不同数据结构题型的下探讨该类问题的解法。

---

打家劫舍1 (数组)

本题只需要讨论当前数组的值取与不取之间的比较。

 	int rob(vector<int>& nums)
	{
		int size = nums.size();
		vector<int> dp(size + 1, 0);
		dp[1] = nums[0];
		for (int i = 2; i <= size; ++i)
		{
			dp[i] = max(dp[i - 1], dp[i - 2] + nums[i - 1]);
		}
		return dp[size];
	}

打家劫舍2（环形数组）

相较于上题，本题需要额外考虑首位两个值取与不取的情况。

	int rob2(vector<int>& nums) 
	{
		int size = nums.size();
		if (size == 1)return nums[0];
		int result;
		vector<int> dp(size + 1, 0);
		dp[1] = nums[0];
		for (int i = 2; i < size; ++i)
			dp[i] = max(dp[i - 1], dp[i - 2] + nums[i - 1]);
		result = dp[size - 1];
		dp[1] = 0;
		for (int i = 2; i <= size; ++i)
			dp[i] = max(dp[i - 1], dp[i - 2] + nums[i - 1]);
		return max(result, dp[size]);
	}

打家劫舍3（二叉树）

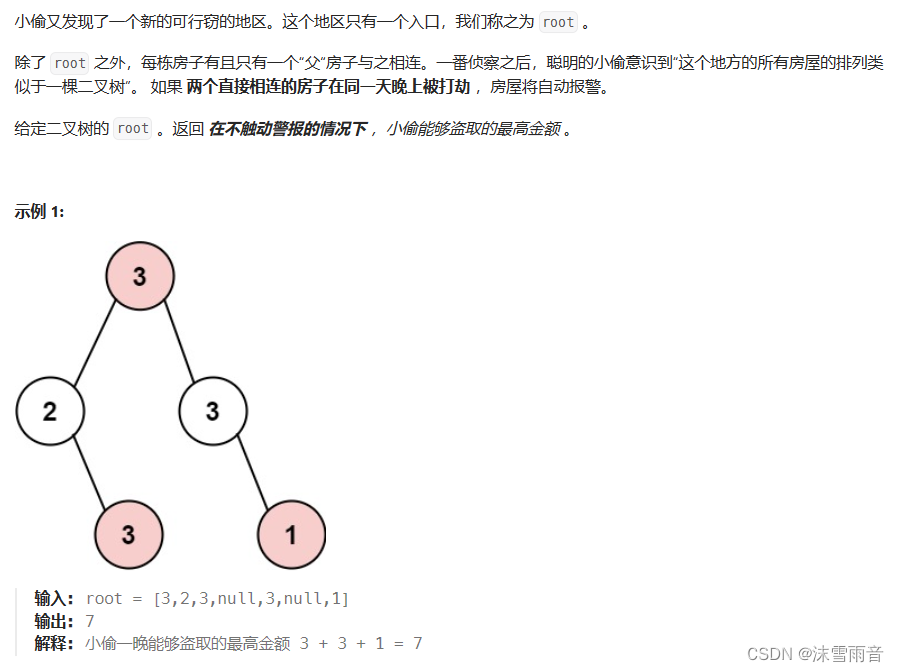
	vector<int> traversal(TreeNode* root)
	{
		if (!root)return {0, 0};
		if (!root->left && !root->right)
			return vector<int> {0, root->val};
		vector<int> left = traversal(root->left);
		vector<int> right = traversal(root->right);
		int val1 = max(left[0], left[1]) + max(right[0], right[1]);
		int val2 = root->val + left[0] + right[0];
		return {val1, val2};
	}
	int rob(TreeNode* root) 
	{
		vector<int> result = traversal(root);
		return max(result[0], result[1]);
	}