排序
下面的代码会用到宏定义,因为再C中没有swap交换函数,所以对于swap的宏定义代码如下:
#define swap(a, b) {\ __typeof(a) __a = a; a = b; b = __a;\ }
稳定排序:
1.插入排序:
插入排序会将数组,分位两个部分,一般分为前后两部分,而前半部分为已排序区,后半部分为未排序区;插入排序的操作就是把,未排序区中的元素插入到已排序区中的去,并且满足排序区的单调性;如图下面的操作,实现一个单调递增序列:
数组的原本样子,现在使位置0是已排序区,先去从位置1开始去插入;
将12插入到23前面,使位置0,1形成单调递增;
进行插入,对位置2插入,发现不用插入,直接对下一个位置进行插入:
位置4也不用进行插入保持原位置,对位置5进行插入:
最后完成排序;
时间复杂度:
代码实现:
void insert_sort(int *arr, int n) {//arr排序数组,n数组长度 for (int i = 1; i < n; i++) {//位置0开始定为已排序区 for (int j = i; j >= 1 && arr[j] < arr[j - 1]; j--) {//将位置i进行插入到前面的以排序区 swap(arr[j], arr[j - 1]);//交换位置 } } return ; }2.冒泡排序:
冒泡排序,为什么会叫冒泡排序,假如实现单调递增序列,那么每一次都会将未排序中的最大的元素放到未排序区中的最后去,把数组立起来数组的最后的位置在上,那么是不是每次未排序的最大元素会像冒泡一样往上升,所以叫冒泡排序;
如图数组最开始状态:
第一次冒泡:
第一次完冒泡后,最大的元素已经放到了数组最后位置,也相当于放到了已排序区中了;然后这样一直循环直到排完序;
时间复杂度:
代码实现:
做了一个小小的优化;
void bubble_sort(int *arr, int n) { int time = 1;//用来标记这次循环是否发生了冒泡交换 for (int i = 1; i < n && time; i++) {//如果没有发生交换说明数组已经排好了序 time = 0; for (int j = 0; j < n - i; j++) { if (arr[j] >= arr[j + 1]) { swap(arr[j], arr[j + 1]); time++; } } } return ; }3.归并排序:
将一个数组从中间分开,然后通过递归一直将子数组进行分开,直到数组只有两个元素,然后通过回溯的过程中进行排序,然后一直回溯到整个数组并拢,完成排序;
如图,将数组这样二分下去:
然后从下往上进行排序,单调递增:
合并,排序:
合并,在排序:
最终完成排序;
时间复杂度:
代码实现:
这个过程比较容易理解,就是代码实现有那么一点复杂,来看代码:
void merge_sort(int *arr, int l, int r) {//数组的头位置,r数组的末尾在 if (r - l <= 1) {//当分到只有2个元素和1个元素时,递归出口 if (r - l == 1 && arr[l] > arr[r]) {//两个元素,进行排序 swap(arr[l], arr[r]); } return ; } int mid = (l + r) >> 1; //开始分列 merge_sort(arr, l, mid);//递归左边数组 merge_sort(arr, mid + 1, r);//递归右边数组 int *temp = (int *)malloc(sizeof(int) * (r - l + 1));//创建一个空间,来存子数组的元素 int p1 = l, p2 = mid + 1, k = 0;//p1数组分裂开的前部分的起始坐标,p2数组分裂开后半部分的起始坐标 while (p1 <= mid || p2 <= r) { if (p2 > r || (p1 <= mid && arr[p1] < arr[p2])) temp[k++] = arr[p1++]; else temp[k++] = arr[p2++]; } memcpy(arr + l, temp, sizeof(int) * (r - l + 1));//将排好序的子数组拷贝给原数组 free(temp); return ; }4.基数排序:
这里假设数组都是两位数,先对数组进行元素的个位进行排序,然后在对数组的十位进行排序,这样就能对数组拍好序;如果位数不相同,取位数最大的数进行位数排序假如最大的位数是3位,那么就进行3次位数排序,如果位数10位那就进行10次位数排序;
如图数组最初:
进行个位排序,上面的表格就是对于个位数的统计,对于排序时会起到作用:

在进行10位排序:
最终完成排序:
时间复杂度:
代码实现:
void number_sort(int *arr, int n, int exp) { int count[10] = {0}; for (int i = 0; i < n; i++) { count[arr[i] / exp % 10] += 1;//对每位数的数的个数统计 } for (int i = 1; i < 10; i++) { count[i] += count[i - 1];//位数排序,从小到大,现在的操作就是使count变为下标 } int *sum = (int *)malloc(sizeof(int) * n); for (int i = n - 1; i >= 0; i--) {//假如个位已近排序后,那么个位大的在后,而根据十位排序也是从高位排到低位,所以需要倒过来存 sum[count[arr[i] / exp % 10] - 1] = arr[i];//下标从0开始,所以需要-1; count[arr[i] / exp % 10]--;//对应的位数已经排序一个,所以数量-1; } memcpy(arr, sum, sizeof(int) * n); free(sum); return ; } void radix_sort(int *arr, int n) { int max = INT_MIN; for (int i = 0; i < n; i++) {//获取最大数的数 max = max > arr[i] ? max : arr[i]; } for (int i = 1; max / i > 0; i *= 10) {//从个位一直到大于最大数的位数 number_sort(arr, n, i); } return ; }非稳定排序:
1.选择排序:
将数组分为两个区域一个已排序区和一个未排序区,每次将未排序区中的最值放在已排序区中;
如图将54放放到最后,也就是已排序区中;
这样一直在未排序区中选择,直到排序完成:
时间复杂度:
代码实现:
void select_sort(int *arr, int n) {//这里实现的是将最小的元素放在最前面,现在前面就是已排序区 for (int i = 0; i < n - 1; i++) { int ind = i;//ind先记录当前准备排序的位置 for (int j = i + 1; j < n; j++) { if (arr[ind] > arr[j]) ind = j;//ind记录未排序区中最小值的值的位置 } swap(arr[ind], arr[i]);//将未排序的区的最小值放在准备排序的位置 } return ; }2.快速排序:
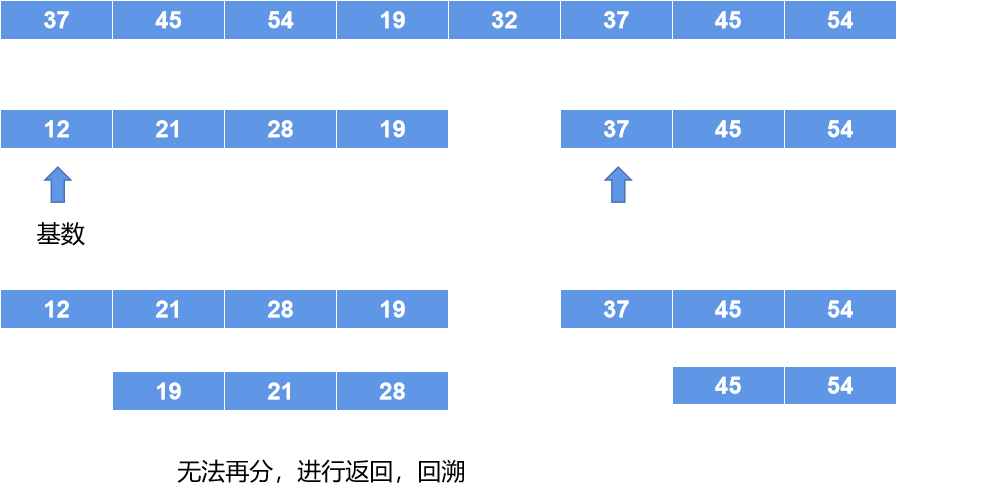
选择数组头步位置,作为基数,用一个变量记录下来,然后将这个基数作为中间值,将数组分为两个部分,前半部分小于这个基数,后半部分大于基数,然后在对两个部分进行上面的操作,直接这两个部分不能再分;这里不一定是二分开的,有可能这个基数是最大值,那么就没有前半部分;
如图数组初始状态:
将32作为基数,把数组分为两部分分:
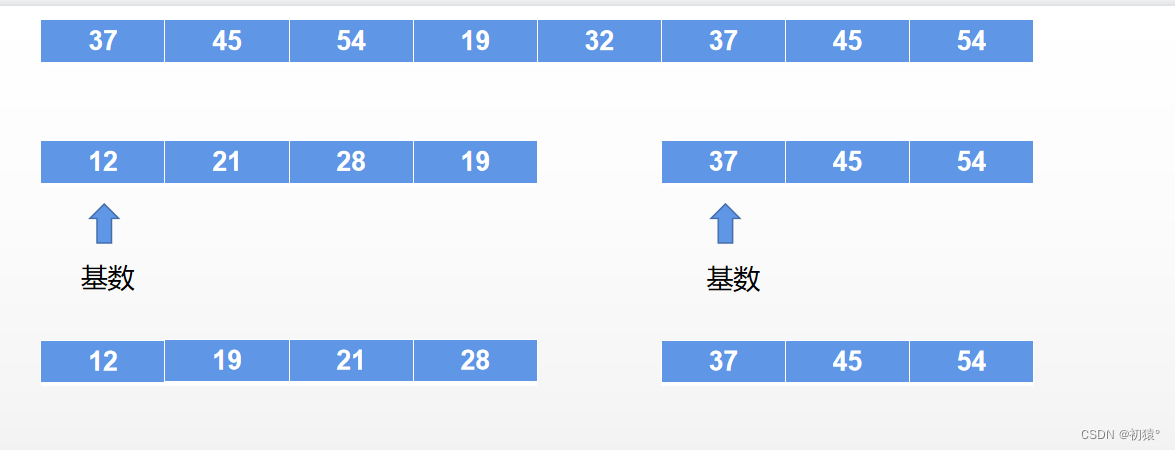
然后再对左边部分进行快排,右边部分进行快排
这里只是刚好,不用变化,然后继续上面的操作,直到最后排完序:
完成排序。
时间复杂度:
最坏:
代码实现:
//l最初为0,r最初为n-1 void quick_sort(int *arr, int l, int r) { if (r < l) return ; int x = l, y = r, num = arr[l]; while (x < y) { while (x < y && arr[y] >= num) y--;//如果大于基数的部分,该位置数大于基数就不用交换 if (x < y) arr[x++] = arr[y];//如果x<y,说明y位置的值是小于基数的,就放到前面去,第一次的时候x的位置就是基数的位置,所以覆盖的是基数的位置 while (x < y && arr[x] <= num) x++;//如果小于基数的部分,该位置数小于等于基数就不用交换 if (x < y) arr[y--] = arr[x];//x<y,说明x位置的值是小于基数的,现在y位置是之前小于基数的位置,直接覆盖 } arr[x] = num;//将基数放到分割位置 quick_sort(arr, l, x - 1);//小于基数的部分 quick_sort(arr, x + 1, r);//大于基数的部分 return ; }3.希尔排序
希尔排序其实就是对于选择排序的一个优化的算法,而最最坏的情况就是降为一个普通的选择排序。
选择一个移动的长度,最开始选择数组长度的1/2,然后一直除2,直到步长等于1,进行一次插入排序;这个步长的作用就是,从一个位置往前移动多少步进行对该位置的值进行比较,如果不满住单调性就进行交换,然后交换如果还能往前目前的步长长度,继续往前比较;
如图,直接上图片理解:
现在的步长选作4,那么就从位置4进行开始排序:
他俩进行比较,然后数组是单调递增,就就需要交换,然后比较位置向后移动:
然后第一次步长结束后,那么步长在除以2:
然后再次进行比较
继续往后
这里发生了交换,而且现在的位置还能往前走步长,所以也需要比较:
比较后,不用发生交换,继续刚刚的位置往后:
这里发生了交换,又需要往前走:
直到不能发生交换,然后现在走到了最后的位置,进行步数除以2,等于1,进行一次选择排序:
这里发生了交换,那就需要再往前走步长那么长进行比较:
最后遍历,没有发生交换,并且步长为除2等于0了,完成排序;
时间复杂度:
最坏:
代码实现:
void shell_sort(int *arr, int n) { int step; for (step = n / 2; step > 0; step >>= 1) {//步长循环 for (int i = step; i < n; i++) {//从步长长度开始往后循环 for (int j = i; j >= step && arr[j] < arr[j - step]; j -= step) { //如果不满足单调性,发生交换,并且如果现在的位置长度大于等于步长继续往前移动进行比较 swap(arr[j], arr[j - step]); } } } return ; }4.堆排序:
堆,堆排序在前面这个链接的文章里,因为单独将堆排序有那么一点难理解需要结合对堆的理解才容易一些;
算法——排序
news2026/2/15 5:29:24
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/954400.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
RS485/RS422 收发器(SIT3485和SIT3485E)
SIT3485 是一款 3.3V 供电、半双工、低功耗,功能完全满足 TIA/EIA-485 标准要求的 RS-485 收发器。 SIT3485 包括一个驱动器和一个接收器,两者均可独立使能与关闭。当两者均禁用时,驱动 器与接收器均输出高阻态。 SIT3485 具有 1…
手把手教你打造自己的AI聊天机器人程序(讯飞星火API)
案例背景
最近发现科大的讯飞星火大模型可以申请API试用了,我一直想用chatgpt的API,一是因为收费买不起,二是因为网络不方便.....
现在有了科大讯飞这个国内免费的,当然要试试。
目前讯飞星火可以申请试用他们的模型API&#x…
影视文化交流:如何通过Netflix了解和欣赏全球不同的影视文化
Netflix成立于1997年,是一家美国的在线流媒体平台。自推出以来,Netflix迅速发展壮大,目前已经成为全球领先的影视内容提供商之一。截至2022年底,Netflix在全球范围内拥有超过2.07亿的付费订阅用户,遍布190多个国家和地区。通过其便捷的平台和丰富的内容库,Netflix为全球观众带来…
Python怎么解决版本兼容性的问题? - 易智编译EaseEditing
Python的版本兼容性问题是在不同Python版本之间代码能否正常运行的问题。由于Python的语言和库在不同版本之间可能存在细微的差异,因此编写能够在多个Python版本上运行的代码是很重要的。
以下是一些解决Python版本兼容性问题的方法:
使用合适的语法&a…
R语言入门——line和lines的区别
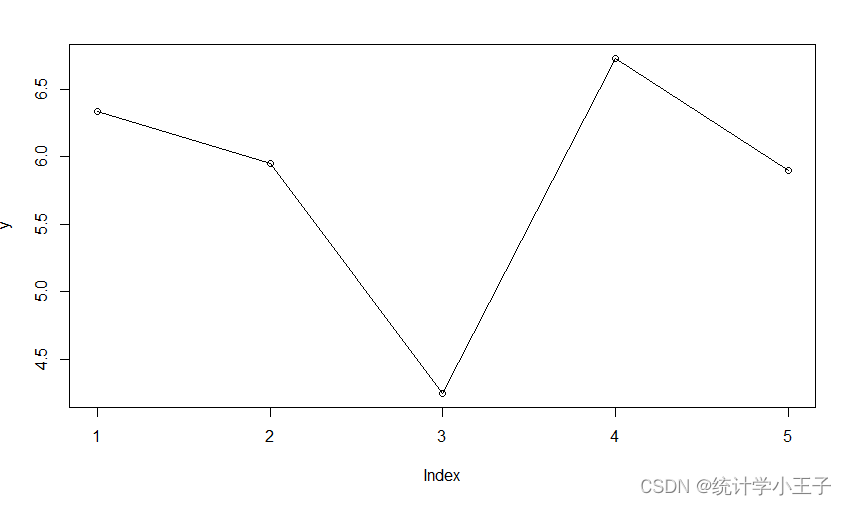
目录 0 引言一、 line()二、 lines() 0 引言
首先,从直观上看,lines比line多了一个s,但它们还是有很大的区别的,下面将具体解释这个两个函数的区别。
一、 line()
从R语言的帮助文档中找到,line()的使用,…
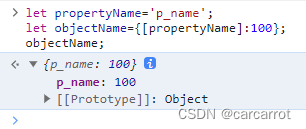
JS小知识点:在定义对象的时候,用变量值作为对象属性名
有没有一种情况,在定义一个对象时,对象的属性名由一个变量的值来决定的?而且是一步到位,简单实现的?
我们知道对象有时被称为关联数组,访问对象属性值的时候可以使用括号表示法(比如 objectNam…
揭秘ChatGPT,如何打造自己的自定义指令 | 京东云技术团队
一、ChatGPT-0720更新
又在深夜,正要打开ChatGPT官网测试下pdf对话功能,发现ChatGPT又有更新。本次更新总结有2点:
1.对于Plus用户,GPT-4的使用限额从25条/3h提升至50条(整整提升1倍~ $20的订阅费又更超值了…
成集云 | 飞书审批同步金蝶云星空 | 解决方案
源系统成集云目标系统 方案介绍
飞书员工报销审批通过后,审批单据内容和审批状态实时同步金蝶云星空
飞书是字节跳动于2016年自研的新一代一站式协作平台,将即时沟通、日历、云文档、云盘和工作台深度整合,通过开放兼容的平台,…
小白学Go基础01-Go 语言的介绍
Go 语言对传统的面向对象开发进行了重新思考,并且提供了更高效的复用代码的手段。Go 语言还让用户能更高效地利用昂贵服务器上的所有核心,而且它编译大型项目的速度也很快。 用 Go 解决现代编程难题
Go 语言开发团队花了很长时间来解决当今软件开发人员…
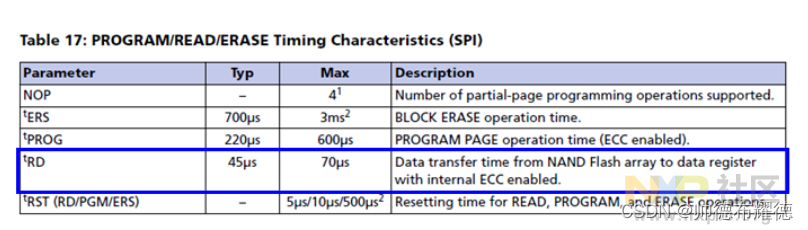
【重要】为什么串行NAND Flash不支持XiP?
并行/串行NOR Flash都支持XIP,但是串行NAND Flash不支持。 今天给大家介绍的是串行NAND Flash的两大特性导致其在i.MXRT FlexSPI下无法XiP。 在嵌入式世界里,当我们提起XiP设备(支持代码原地执行的存储器),首先想到的应…
从传统到智能化:汽车内部通信的安全挑战与SecOC解决方案
01/需求背景
Demand background
在传统的汽车电子结构中,车内的电控单元(ECU)数量和复杂性受到限制,通信带宽也受到限制。因此,人们普遍认为车内各个ECU之间的通信是可靠的。只要ECU节点接收到相应的消息,…
[ROS]虚拟机ubuntu18.04系统里面运行usb_cam
首先安装usb_cam
sudo apt-get install ros-melodic-usb-cam
运行:
roscore
roslaunch usb_cam usb_cam-test.launch
如果一运行报错,首先确认是否存在/dev/video0
可以使用ls /dev/video*查看,如果没有就是没有连接摄像头,…
ChatGPT总结(持续更新)
目录
体验渠道
weTab
CSDN-AI助手
其他插件
ChatGPT简介
ChatGPT主要用途
ChatGPT发展历程
GPT-4架构的特点和优势
ChatGPT的工作原理
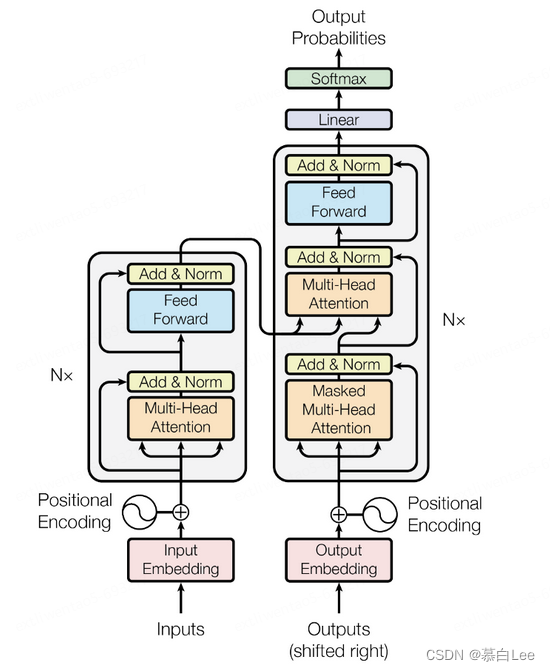
神经网络和自然语言处理技术
Transformer模型
模型训练优化技巧
ChatGPT对程序员的帮助
与ChatGPT交互和提问技巧
ChatGPT未来…
中国移动携手移远通信等合作伙伴发布 RedCap“1+5+5”创新示范之城
日前,《关于推进5G轻量化(RedCap)技术演进和应用创新发展的通知(征求意见稿)》正式公布,将进一步推进5G RedCap 技术演进、产品研发及产业化,大力推动5G应用规模化发展。
为加快推动RedCap规模…
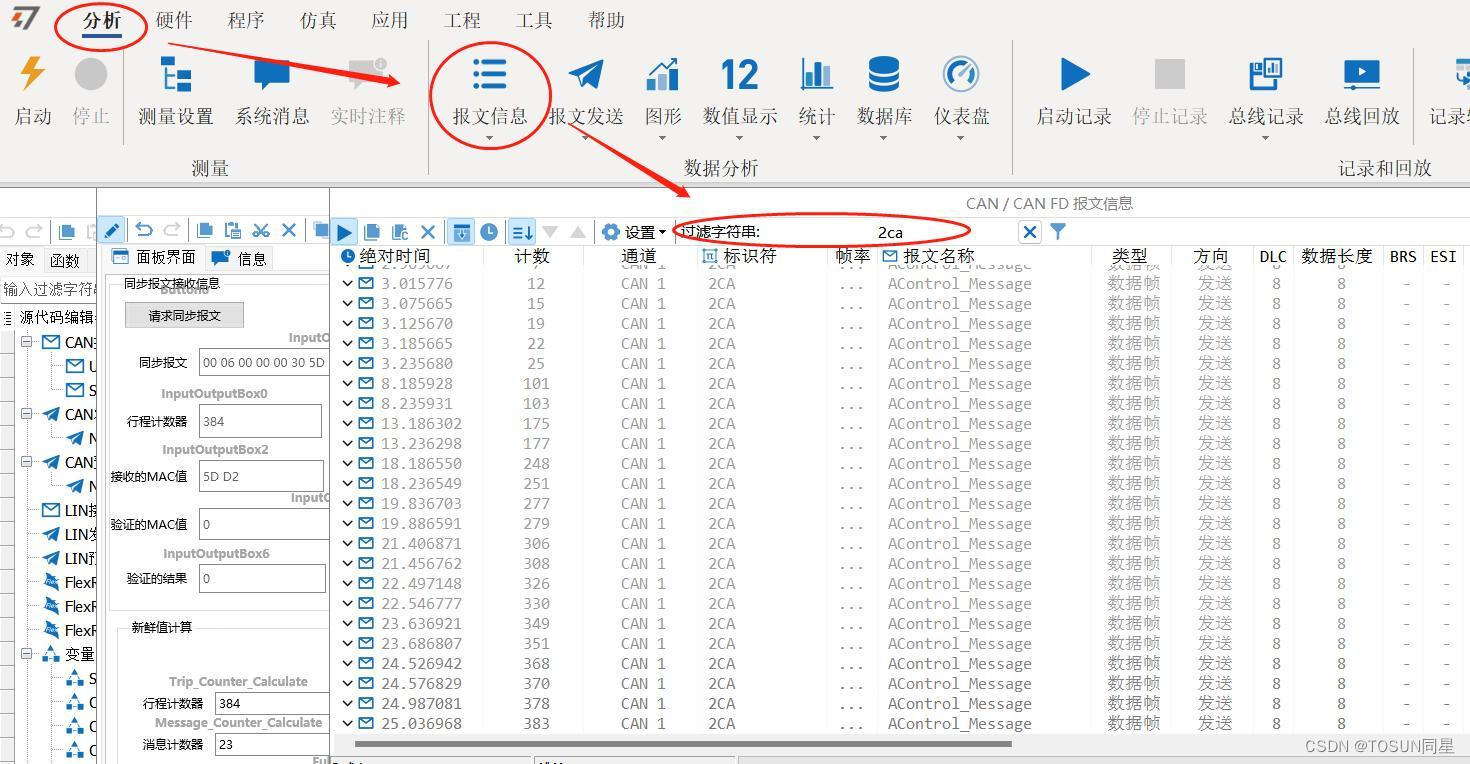
TSMaster小功能分享—Python小程序如何导入外部库
今天给大家介绍TSMaster功能之Python小程序如何导入外部库。通过在 TSMaster 默认的解析器路径下导入外部库来介绍,以便我们去使用 Python 外部库。TSMaster 默认 Python 解析器下安装外部库。 步骤一
在 TSMaster 工具->系统信息->python 环境设置中选择打开…
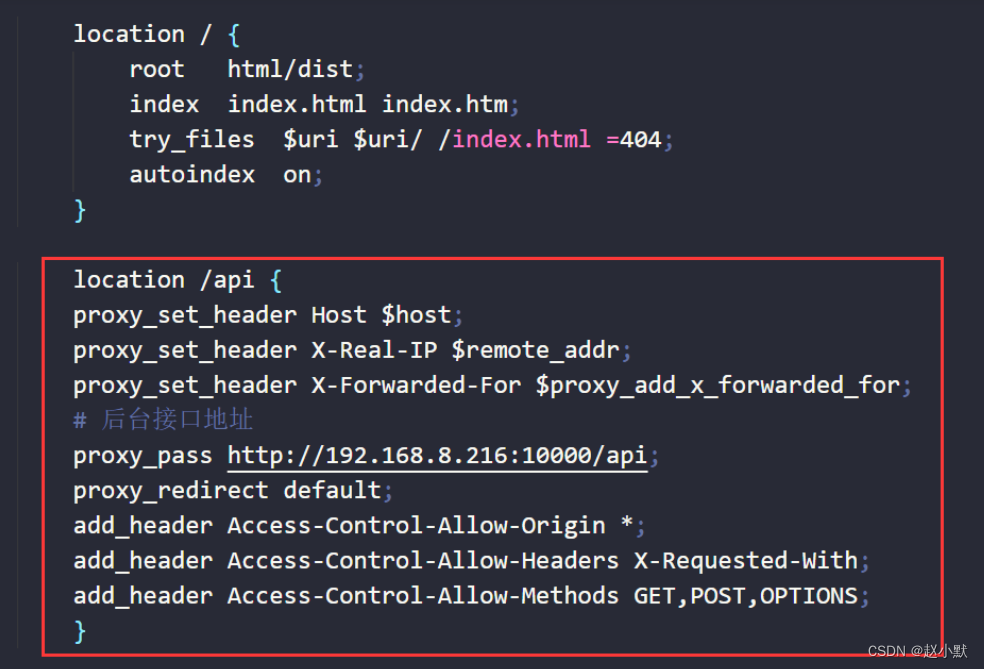
Windows安装Nginx及部署vue前端项目操作
先在nginx官网下载windows下安装的包,并解压,到ngnix目录下 双击nginx.exe,会有黑窗闪过。 用cmd命令窗口,cd 到nginx解压目录,./nginx启动。 在浏览器中访问http://localhost:80,出现以下界面说明启动成功(由于笔者电脑80端口被…
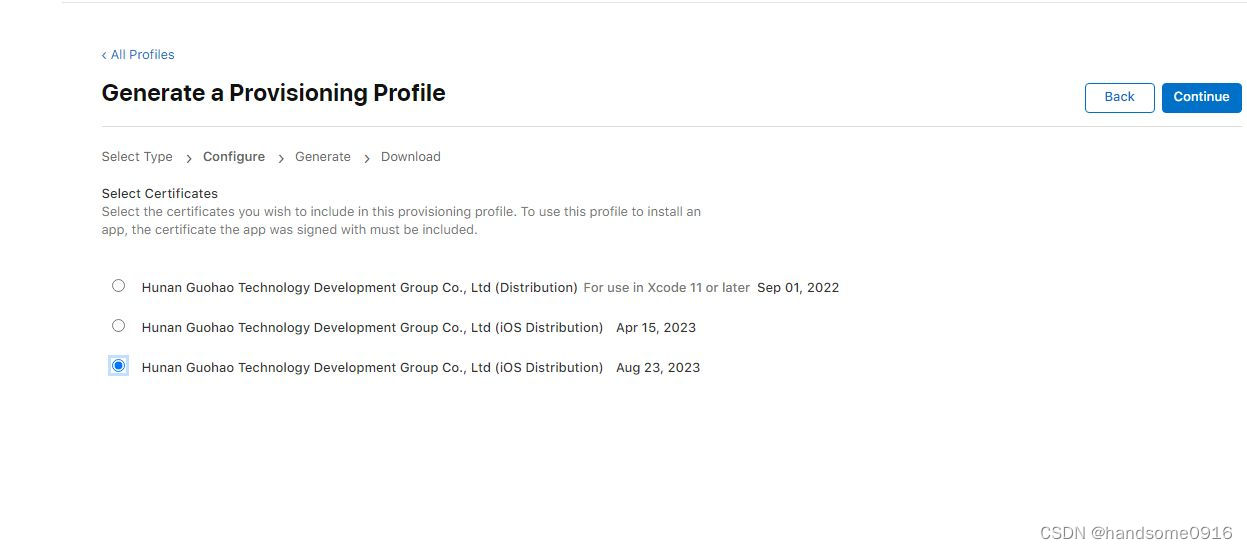
windows生成ios证书的方法
使用hbuilderx的uniapp框架开发ios应用,在测试阶段和发布阶段,需要ios证书进行打包,云打包的界面提供了生成ios证书的教程,但是教程令人很失望,它只能使用mac电脑来生成ios证书。假如没有mac电脑,就无法安照…
RK3562 VS RK3566 性能解析
RK3562是深圳触觉智能最新推出的一款高性能核心板及其开发套件,采用四核A53Mali G52架构,主频2GHz,内置1T NPU算力以及13M ISP,拥有丰富的外围接口。其次在解码方面,支持H.264 1080P60fps、H.265 4K30fps;编…





































![[ROS]虚拟机ubuntu18.04系统里面运行usb_cam](https://img-blog.csdnimg.cn/0075c472f40a49ffa79dd9e0852de06a.jpeg)