1.算法描述

智能控制的思想最早来自傅京孙教授[，他通过人机控制器和机器人方面的研究，首先把人工智能的自觉推理方法用于学习控制系统，将智能控制概括为自动控制和人工智能的结合。他认为低层次控制中用常规的基本控制器，而高层次的智能决策应该具有拟人化功能。J．M．Mendel教授进一步在空间飞行器的学习控制中应用了人工智能技术，并提出了人工智能的概念。1976年，Leondes和Mendel首次正式使用了人工智能控制一词。从70年代开始傅京孙、Glorioso和Saridi等人从控制理论的角度总结了人工智能技术与自适应、自学习和自组织控制的关系，正式提出建立智能控制理论的构想。1985年8月在美国纽约PRI、IEEE召开的智能控制专题讨论会，标志着智能控制作为一个新的学科分支正式被控制界公认。从1987年开始，每年都举行一次智能控制国际研讨会，形成了智能控制的研究热潮。80年代以来微机的高速发展为实用的智能控制器的研制及智能控制系统的开发提供了技术基础。人工智能技术中关于知识表达、推理技术以及专家系统的设计与建造方面的技术进展也为智能控制系统的研究和开发准备了新的条件和途径，出现了专家控制系统并在工业过程控制、航空航天技术和军事决策等方面实际应用，取得了引人注目的应用成果。

近年来，随着对智能控制方法的深入研究，在板形板厚控制方面已开发出各种智能控制器。在利用轧机出口侧的测厚仪进行厚度反馈的AGC系统中，由于测厚仪与辊缝有一段较大的距离，因而检测的厚度偏差具有时滞性，无法消除一些呈周期性频繁变化的因素对轧件出口厚度的影响。而且，由于取样和控制周期长，从而增加了带头、带尾不合格部分的长度，使成材率降低。为此，后续开发的AGC系统力图对出口辊缝的带钢厚度进行检测和控制。目前比较成熟的有辊缝控制法、厚度计法及秒流量法。文献[19]设计了一种新型的基于遗传算法的多变量模糊控制器，通过结合模糊预测和遗传算法来优化控制规律，利用遗传算法来辨识系统参数。文中提出的辨识方法是成功的，但是在模糊模型的辨识中也存在着以下问题：(1)模糊模型结构的辨识方法不是简单易行；(2)如何进一步改进遗传学习算法，以便加快学习的收敛速度。文献[21]针对被控对象轧制过程中参数，AGC系统采用了PID在线辨识自校正控制技术，取得了很好的控制效果。该方法有很强的针对性，没有很好的解决非线性、强耦合问题。文献]采用人工神经网络技术与预测控制及控制相结合的方法，提出了一种基于结构化多层前向神经网络的次优控制器设计方案，通过对板厚板形综合系统的仿真研究表明，系统不需解耦即可获得满意的控制精度和稳定的鲁棒性。近年来国内在这方面也有很多成果，文献[14]将模糊技术与神经网络技术相结合，提出了一种模糊神经网络解耦控制方法进行板形板厚控制也有不错的效果。

结构为：

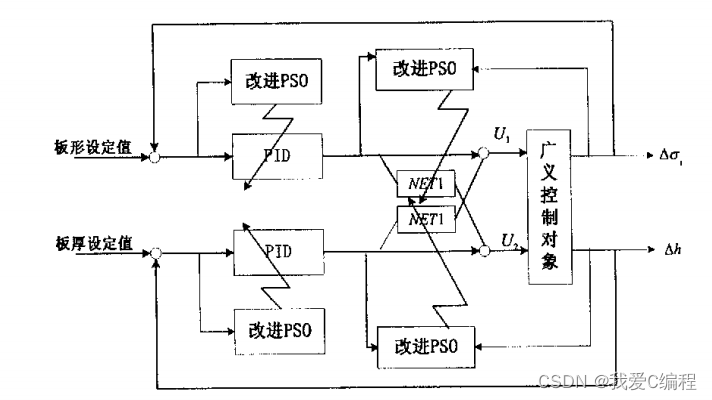
PSO算法是Keimedy和Eberhart于1995年提出来的。由于该算法实现简单，搜索能力强。目前已经得到了广泛的应用。其中几个有代表性的例子：

1．利用PSO算法代替误差反向传播算法来训练神经网络。研究表明PSO算法是一种很有潜力的神经网络学习算法。PSO算法速度比较快而且可以得到比较好的结果，还没有遗传算法碰到的问题[28]。PSO算法被用于选择BP神经元网络的权值[24,27]。文献[24]使用BP神经网络的输入层、隐含层和输出层分别有5个、3个和1个神经元，实验结果证明了PSO算法跟BP算法相比的优越性。此外，用PSO算法训练进化神经网络的另一个成功例子是用于分析人的颤抖。对人的颤抖的诊断，包括帕金森(Parkinson)病和原发性振颤(Essential Tremor)，是一个非常有挑战性的领域[26]。

2．PSO算法用于计算机数字控制研磨优化[29]。因为多点金属切割的过程基本原理还未被很好的理解，同时也由于这一过程的高度非线性特性。而使用PSO优化进行的网络权值进化提供了一种准确可靠的方法。完成终端研磨操作所需时间显著减少，这导致总体成本降低，同时得到更好的研磨质量。这一概念正被扩展到其他的机器制造过程以及复杂过程参数集的预测和优化。

3．PSO算法也被成功的应用于电力系统领域[30]。日本学者Fukuyama等人使用PSO算法对一个电力系统的动态稳定性参数进行优化。这里主要涉及到带有约束条件的、使用不同版本的PSO算法相结合用来决定对连续和离散控制变量的控制策略的问题。此外，余欣梅等人用PSO算法解决电容器优化配置问题很好的获得了电容器优化配置问题的全局最优解。

2.仿真效果预览

matlab2022a仿真结果如下：

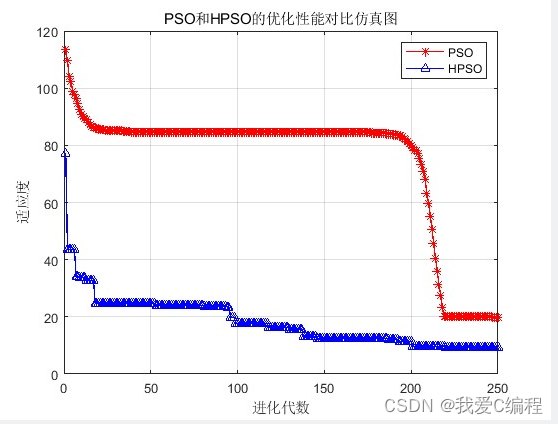
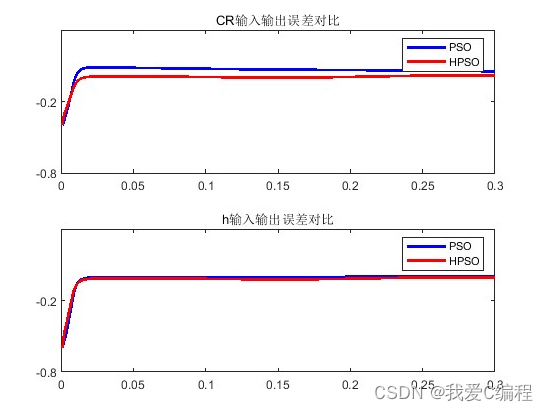
3.MATLAB核心程序


if sel == 1
   %输入的CR和h
   %分别仅输入CR和h，使其达到解耦的结果
   [yy,Zbest] = func_train_onlineHPSO(iteration,Sizes,CR,h);
   figure(1)
   plot(yy,'LineWidth',2);grid on;
   xlabel('进化代数');
   ylabel('适应度');
   individual=Zbest;
   save trainHPSO.mat Zbest yy
else
   load trainHPSO.mat
   figure(1)
   plot(yy,'LineWidth',2);grid on;
   xlabel('进化代数');
   ylabel('适应度');
   individual=Zbest; 
end


 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%以下为RBF%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
w11=reshape(individual(1:6),3,2);
w12=reshape(individual(7:12),3,2);
w13=reshape(individual(13:18),3,2);

w21=individual(19:27);
w22=individual(28:36);
w23=individual(37:45);

rate1=0.006;rate2=0.001; %学习率
k=0.3;K=3;
y_1=zeros(3,1);y_2=y_1;y_3=y_2;   %输出值
u_1=zeros(3,1);u_2=u_1;u_3=u_2;   %控制率
h1i=zeros(3,1);h1i_1=h1i;  %第一个控制量
h2i=zeros(3,1);h2i_1=h2i;  %第二个控制量
h3i=zeros(3,1);h3i_1=h3i;  %第三个空置量
x1i=zeros(3,1);x2i=x1i;x3i=x2i;x1i_1=x1i;x2i_1=x2i;x3i_1=x3i;   %隐含层输出 

%权值初始化
k0=0.03;

%值限定
ynmax=1;ynmin=-1;  %系统输出值限定
xpmax=1;xpmin=-1;  %P节点输出限定
qimax=1;qimin=-1;  %I节点输出限定
qdmax=1;qdmin=-1;  %D节点输出限定
uhmax=1;uhmin=-1;  %输出结果限定

for k=1:1:6000
    k
    %系统输出
    y1(k) = (0.4*y_1(1)+u_1(1)/(1+u_1(1)^2)+0.2*u_1(1)^3+0.5*u_1(2))+0.3*y_1(2);
    y2(k) = (0.4*y_1(2)+u_1(2)/(1+u_1(2)^2)+0.2*u_1(2)^3+0.5*u_1(1))+0.3*y_1(1);
    y3(k) = 0;
    
    
    %控制目标
    if selt == 1%加扰测试
        r1(k)  = CR + 0.005*sin(2*pi*k/200);
        r2(k)  = h  + 0.015*sin(2*pi*k/200);
        r3(k)  = 0; 
        r1s(k) = CR;
        r2s(k) = h;
        r3s(k) = 0;         
    else        %跟踪测试
        r1(k)  = sign(0.001*sin(2*pi*k/2000));
        r2(k)  = sign(0.003*sin(2*pi*k/2000));
        r3(k)  = 0;      
        r1s(k) = CR;
        r2s(k) = h;
        r3s(k) = 0;    
    end
    
    
    %系统输出限制
    yn=[y1(k),y2(k),y3(k)];
    yn(find(yn>ynmax))=ynmax;
    yn(find(yn<ynmin))=ynmin;
    
    %输入层输出
    x1o=[r1(k);yn(1)];
    
    x2o=[r2(k);yn(2)];
    
    x3o=[r3(k);yn(3)];
    
    %隐含层 
    x1i=w11*x1o;
    x2i=w12*x2o;
    x3i=w13*x3o;

    %比例神经元P计算
    xp=[x1i(1),x2i(1),x3i(1)];
    xp(find(xp>xpmax))=xpmax;
    xp(find(xp<xpmin))=xpmin;
    qp=xp;
    h1i(1)=qp(1);
    h2i(1)=qp(2);
    h3i(1)=qp(3);

    %积分神经元I计算
    xi=[x1i(2),x2i(2),x3i(2)];
    qi=[0,0,0];
    qi_1=[h1i(2),h2i(2),h3i(2)];
    
    qi=qi_1+xi;
    qi(find(qi>qimax))=qimax;
    qi(find(qi<qimin))=qimin;
    h1i(2)=qi(1);
    h2i(2)=qi(2);
    h3i(2)=qi(3);

    %微分神经元D计算
    xd=[x1i(3),x2i(3),x3i(3)];
    qd=[0 0 0];
    xd_1=[x1i_1(3),x2i_1(3),x3i_1(3)];
    qd=xd-xd_1;
    qd(find(qd>qdmax))=qdmax;
    qd(find(qd<qdmin))=qdmin;
    h1i(3)=qd(1);
    h2i(3)=qd(2);
    h3i(3)=qd(3);

    %输出层计算
    wo=[w21;w22;w23];
    qo=[h1i',h2i',h3i'];
    qo=qo';
    uh=wo*qo;
    uh(find(uh>uhmax))=uhmax;
    uh(find(uh<uhmin))=uhmin;
    u1(k)=uh(1);
    u2(k)=uh(2);
    u3(k)=uh(3);  

    
    %计算误差
    error=[r1(k)-y1(k);r2(k)-y2(k);0];  
    error1(k)=error(1);error2(k)=error(2);error3(k)=0;
    J(k)=0.5*(error(1)^2+error(2)^2);   %调整大小
    ypc=[y1(k)-y_1(1);y2(k)-y_1(2);y3(k)-y_1(3)];
    uhc=[u_1(1)-u_2(1);u_1(2)-u_2(2);u_1(3)-u_2(3)];
    
    %隐含层和输出层权值调整

    %调整w21
    Sig1=sign(ypc./(uhc(1)+0.00001));
    dw21=sum(error.*Sig1)*qo';  
    w21=w21+rate2*dw21;
    
    %调整w22
    Sig2=sign(ypc./(uh(2)+0.00001));
    dw22=sum(error.*Sig2)*qo';
    w22=w22+rate2*dw22;
    
    %调整w23
    Sig3=sign(ypc./(uh(3)+0.00001));
    dw23=sum(error.*Sig3)*qo';
    w23=w23+rate2*dw23;

    %输入层和隐含层权值调整
    delta2=zeros(3,3);
    wshi=[w21;w22;w23];
    for t=1:1:3
        delta2(1:3,t)=error(1:3).*sign(ypc(1:3)./(uhc(t)+0.00000001));
    end
    for j=1:1:3
        sgn(j)=sign((h1i(j)-h1i_1(j))/(x1i(j)-x1i_1(j)+0.00001));
    end
 
     s1=sgn'*[r1(k),y1(k)];
     wshi2_1=wshi(1:3,1:3);
     alter=zeros(3,1);
     dws1=zeros(3,2);
     for j=1:1:3
         for p=1:1:3
             alter(j)=alter(j)+delta2(p,:)*wshi2_1(:,j);
         end
     end
     
     for p=1:1:3
         dws1(p,:)=alter(p)*s1(p,:);
     end
     w11=w11+rate1*dws1;

     %调整w12
    for j=1:1:3
        sgn(j)=sign((h2i(j)-h2i_1(j))/(x2i(j)-x2i_1(j)+0.0000001));
    end
    s2=sgn'*[r2(k),y2(k)];
    wshi2_2=wshi(:,4:6);
    alter2=zeros(3,1);
    dws2=zeros(3,2);
    for j=1:1:3
        for p=1:1:3
            alter2(j)=alter2(j)+delta2(p,:)*wshi2_2(:,j);
        end
    end
    for p=1:1:3
        dws2(p,:)=alter2(p)*s2(p,:);
    end
    w12=w12+rate1*dws2;
    
    %调整w13
    for j=1:1:3
        sgn(j)=sign((h3i(j)-h3i_1(j))/(x3i(j)-x3i_1(j)+0.0000001));
    end
    s3=sgn'*[r3(k),y3(k)];
    wshi2_3=wshi(:,7:9);
    alter3=zeros(3,1);
    dws3=zeros(3,2);
    for j=1:1:3
        for p=1:1:3
            alter3(j)=(alter3(j)+delta2(p,:)*wshi2_3(:,j));
        end
    end
    for p=1:1:3
        dws3(p,:)=alter2(p)*s3(p,:);
    end
    w13=w13+rate1*dws3;

    %参数更新
    u_3=u_2;u_2=u_1;u_1=uh;
    y_2=y_1;y_1=yn;
    h1i_1=h1i;h2i_1=h2i;h3i_1=h3i;
    x1i_1=x1i;x2i_1=x2i;x3i_1=x3i;
    
    ErrCr(k) = y1(k) - r1s(k);
    Errh(k)  = y2(k) - r2s(k);
end