题目:
给定一个矩阵m,从左上角开始每次只能向右或者向下走,最后到达右下角的位置,路径上所有的数字累加起来就是路径和,返回所有路径中最小的路径和。
示例:
给定的m如下:
1 3 5 9
8 1 3 4
5 0 6 1
8 8 4 0
红色1 3 1 0 6 1 0为最短路径,和为12。
分析:

最后求得的矩阵 dp 如下:
1 4 9 18
9 5 18 12
14 5 11 12
22 13 15 12
代码实现:
public static int minPathSum1(int[][] m) {
//如果矩阵为空 或者行数为0 列数为0
if (m == null || m.length == 0 || m[0] == null || m[0].length == 0) {
return 0;
}
int row = m.length;//行数
int col = m[0].length; //列数
int[][] dp = new int[row][col];//初始化dp矩阵
dp[0][0] = m[0][0];
//for循环得到dp矩阵第一列的值
for (int i = 1; i < row; i++) {
dp[i][0] = dp[i -1][0] + m[i][0];
}
//for循环得到dp矩阵第一行的值
for (int j = 1; j < col; j++) {
dp[0][j] = dp[0][j-1] + m[0][j];
}
//for循环得到其他位置的最短路径和
for (int i = 1; i < row; i++) {
for (int j = 1; j < col; j++) {
dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + m[i][j];
}
}
return dp[row-1][col-1];
}进行空间压缩:
使用一个arr数组,不断滚动,最开始是[0,0,0,0],然后变成dp矩阵第一行、dp矩阵第二行、最后变成dp矩阵的最后一行。

 代码实现:
代码实现:
public static int minPathSum2(int[][] m) {
if (m == null || m.length == 0 || m[0] == null || m[0].length == 0) {
return 0;
}
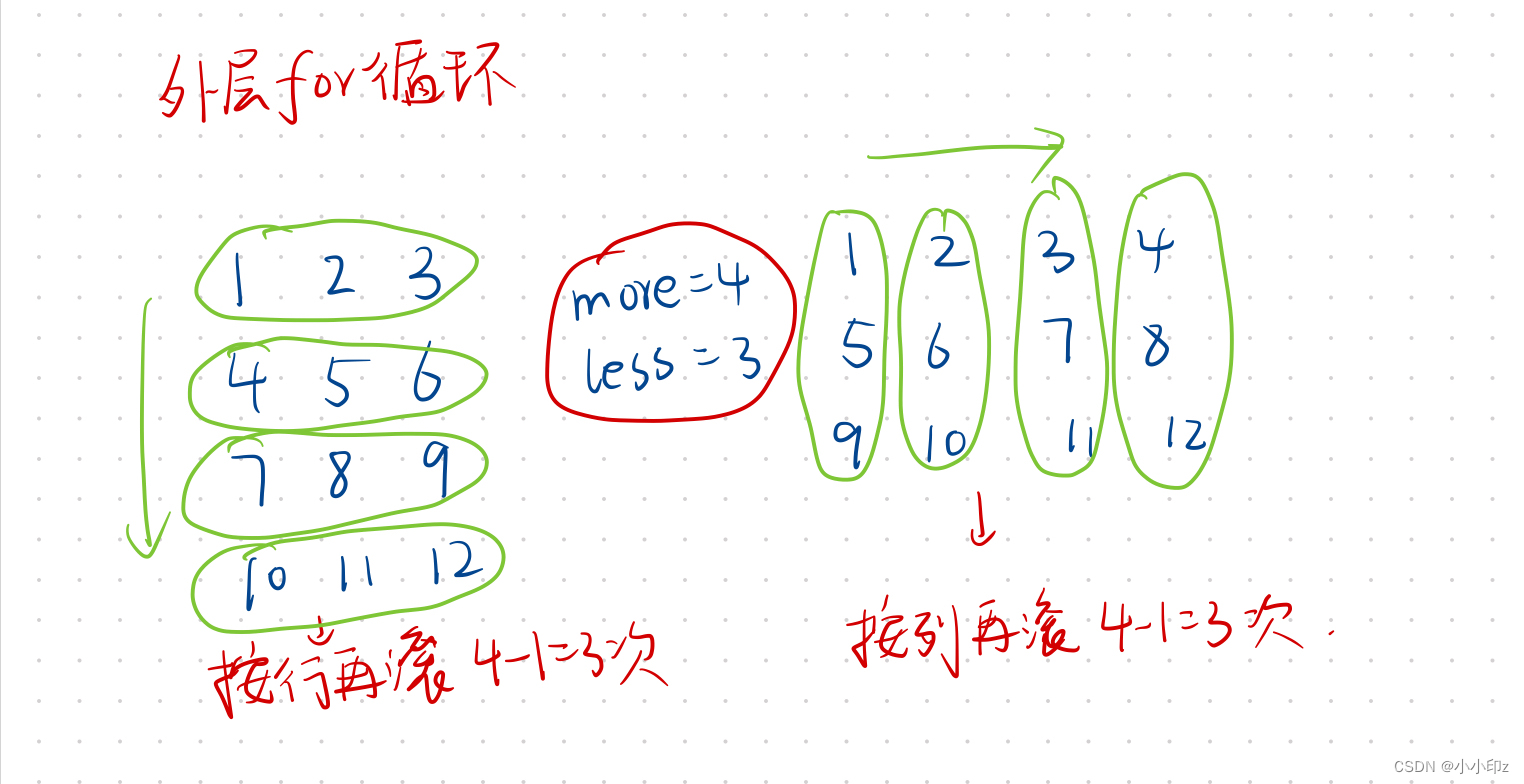
//得到行数和列数 more是大的数 less是小的数
int more = Math.max(m.length, m[0].length);
int less = Math.min(m.length, m[0].length);
//行数是不是大于或等于列数
// 比如4行3列,那么more=4,m.length=4,4==4,返回true,说明行数大于等于列数
// 比如3行4列,那么more=4,m.length=3,4!=3,返回false,说明行数不大于等于列数
boolean rowmore = more == m.length;
int[] arr = new int[less];
arr[0] = m[0][0];
//根据rowmore的值来决定按dp矩阵的行往下滚还是按列往下滚
for (int i = 1; i < less; i++) {
arr[i] = arr[i-1] + (rowmore ? m[0][i] : m[i][0]);
}
//开始往下滚
for (int i = 1; i < more; i++) {
//arr[0] = arr[0](上一个arr[0]) + m[i][0]; 按行滚
//或者 arr[0] = arr[0](上一个arr[0]) + m[0][i]; 按列滚
arr[0] = arr[0] + (rowmore ? m[i][0] : m[0][i]);
//开始求 arr[1],arr[2]...
for (int j = 1; j < less; j++) {
arr[j] = Math.min(arr[j-1],arr[j]) + (rowmore ? m[i][j] : m[j][i]);
}
}
return arr[less-1];
}对于第一个for循环:

对于第二个for循环(外层和内层)