BellmanFord算法与SPFA算法
展开

Bellman-Ford
Bellman-Ford 算法是一种用于计算带权有向图中单源最短路径(SSSP:Single-Source Shortest Path)的算法。该算法由 Richard Bellman 和 Lester Ford 分别发表于 1958 年和 1956 年,而实际上 Edward F. Moore 也在 1957 年发布了相同的算法,因此,此算法也常被称为 Bellman-Ford-Moore 算法。
Bellman-Ford 算法和 Dijkstra 算法同为解决单源最短路径的算法。对于带权有向图 G = (V, E),Dijkstra 算法要求图 G 中边的权值均为非负,而 Bellman-Ford 算法能适应一般的情况(即存在负权边的情况)。一个实现的很好的 Dijkstra 算法比 Bellman-Ford 算法的运行时间要低。
基本概念
负权边:权值为负数的边,称为负权边。
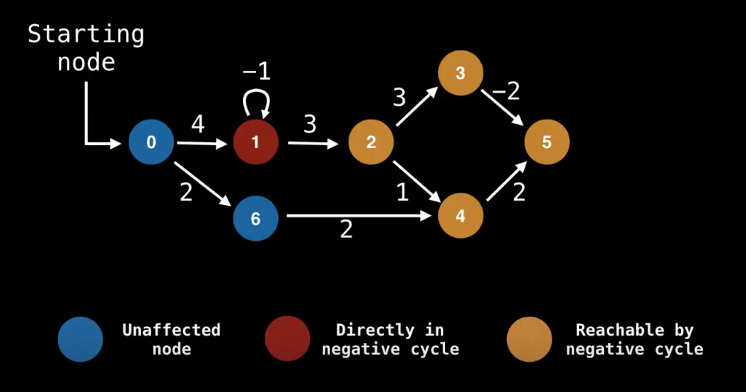
负环:环路中所有边的权值之和为负数,则称该环路为负环。
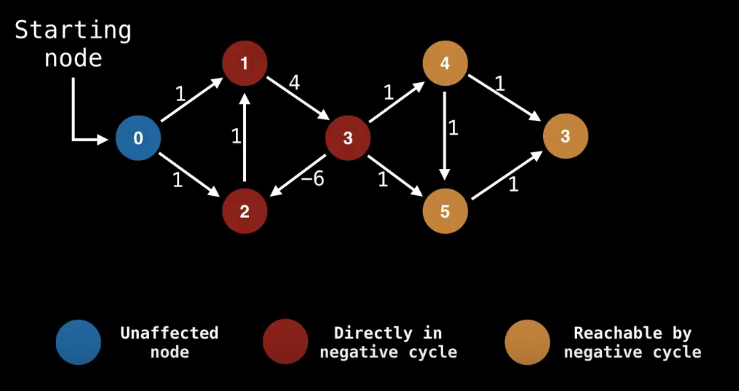
注意:带负环的图无法求最短路,因为可以沿着负环不停的循环,最短距离为负无穷大。
算法步骤
Bellman-Ford 算法采用动态规划(Dynamic Programming)进行设计,实现的时间复杂度为 O(V*E)O(V∗E),其中 VV 为顶点数量,EE 为边的数量。Dijkstra 算法采用贪心算法(Greedy Algorithm)范式进行设计,普通实现的时间复杂度为 O(V^2)O(V2),若基于堆优化的最小优先队列实现版本则时间复杂度为 O(E + VlogV)O(E+VlogV)。
Bellman-Ford 算法描述:
- 创建源顶点 v 到图中所有顶点的距离的集合 dis[]dis[],为图中的所有顶点指定一个距离值,初始均为 ∞∞,源顶点距离为 00;
- 计算最短路径,执行 V - 1V−1 次遍历(松弛边);
- 对于图中的每条边:如果起点 uu 的距离 dd 加上边的权值 ww 小于终点 vv 的距离 dd,则更新终点 vv的距离值 dd;
- 检测图中是否有负权边形成了环,遍历图中的所有边,如果 dis[e.u]+e.w < dis[e.v]dis[e.u]+e.w<dis[e.v],则说明存在环;
模板题
Dijkstra求最短路 I - TopsCoding
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
int n, m, k;
struct Edge{
int u,v,w;
}e[N];
int dis[N];
void bf(int s)
{
memset(dis, 0x3f, sizeof dis);
dis[s] = 0;
for(int i = 1; i < n; i++)
for(int j = 1; j <= m; j++)
{
if(e[j].v == e[j].u) continue; // 有自环不受影响,本条语句可以注释
dis[e[j].v] = min(dis[e[j].v], dis[e[j].u] + e[j].w);
}
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= m; i++)
cin >> e[i].u>>e[i].v>>e[i].w;
bf(1);
if(dis[n] < 0x3f3f3f3f/2) cout << dis[n];
else cout << -1;
return 0;
}
Copy
思考
-
为什么要循环 n-1n−1 次? 【回答】:因为最短路径肯定是个简单路径,不可能包含回路的。而图有 nn 个点,又不能有回路 所以最短路径最多 n-1n−1 边,又因为每次循环,至少松弛了一条边 所以最多 n-1n−1 次就行了。
-
为什么Dijkstra无法处理负边,而Bellman-Ford可以处理负边?【回答】:Dijkstra本质上是一种贪心策略,当有负边存在时,局部最优无法带来全局最优,贪心失效。
Bellman-Ford本质上是一种枚举策略,在求解s →0的最短路径时,会计算所有s → b的不包含环路的路径,从中挑出权值和最小的路径。
有边数限制的最短路
问题:有边数限制的最短路 - TopsCoding
碰到限制了最短路径上边的数量时就只能用 bellman-ford 了,此时直接把上面代码中的 nn 重循环改成 kk 次循环即可
#include<bits/stdc++.h>
using namespace std;
const int N=510, M=10010;
struct Edge{
int a;
int b;
int w;
}e[M]; //把每个边保存下来即可
int dis[N];
int back[N]; // 备份数组放置串联
int n,m,k; // k代表最短路径最多包涵k条边,k=n-1意味着裸最短路
int bellman_ford(int s){
memset(dis, 0x3f, sizeof dis);
dis[s]=0;
for(int i=1;i<=k;i++){ // k次循环
memcpy(back,dis,sizeof dis); // 备份上一次更新后的距离数组
for(int j=1;j<=m;j++){ //遍历所有边
int a=e[j].a,b=e[j].b,w=e[j].w;
dis[b]=min(dis[b],back[a]+w); //使用backup原因:避免给a更新后立马更新b,这样就串联更新了
}
}
if(dis[n]>0x3f3f3f3f/2) return -1; // 因为存在负权边,所以无法到达的节点的 dis[] 可能比 0x3f3f3f3f 要小
else return dis[n];
}
int main(){
cin >> n >> m >> k;
for(int i=1;i<=m;i++){
cin >> e[i].a >> e[i].b >> e[i].w;
}
int res=bellman_ford(1);
if(res==-1) puts("impossible");
else cout<<res;
return 0;
}
Copy
值得注意的是:
1) 需要把 disdis 数组进行一个备份,这样防止每次更新的时候出现串联;
2) 由于存在负权边,所以无法到达的节点的 dis[]dis[] 可能比 0x3f3f3f3f0x3f3f3f3f要小,因此无法到达的判断条件要改成 dist[n]>0x3f3f3f3f/2;
3) 上面所谓的 nn 次遍历的实际含义是当前的最短路径最多有 n-1n−1 条边,这也就解释了为啥要 ii 遍历到 nn 的时候退出循环了,因为只有 nn 个点,最短路径无环最多就存在 n-1n−1 条边。
4) 这里无需对重边和自环做单独的处理:a. 重边:由于遍历了所有的边,总会遍历到较短的那一条; b. 自环: 有自环就有自环啊,反正又不会死循环;
5) bellman-ford 算法可以存在负权回路,因为它求得的最短路是有限制的,是限制了边数的,这样不会永久的走下去,会得到一个解
6) SPFA算法各方面优于该算法,但是在碰到限制了最短路径上边的长度时就只能用 bellman-ford了,此时直接把 nn 重循环改成 kk 次循环即可。
拓展
视频讲解:Bellman Ford 单源最短路径算法【英文中字】_bilibili
SPFA
基本原理
Bellman Ford + 队列优化 = SPFA
SPFA 算法的英文全称是 Shortest Path Faster Algorithm,从名字上我们就看得出来这个算法的最大特点就是快。它比 Bellman-ford 要快上许多倍,它的复杂度是,这里的 k是一个小于等于2的常数。
SPFA 的核心原理和 Bellman-ford 算法是一样的,也是对点的松弛。只不过它优化了复杂度,优化的原理很简单, 只有被松弛过的点才有可能去松弛其他的点。优化的方法也很简单,用一个队列维护了可能存在新的松弛的点,这样我们每次从这些点出发去寻找其他可以松弛的点加入队列。
SPFA 的代码也很短,实现起来难度很低,单单从代码上来看和普通的宽搜区别并不大。
算法步骤
- 建立一个表格记录起始点到所有点的最短路径(该表格的初始值要赋为极大值,该点到他本身的路径赋为0)。
- 建立一个队列,初始时队列里只有起始点。
- 执行松弛操作,用队列里有的点作为起始点去刷新到所有点的最短路,如果刷新成功且被刷新点不在队列中则把该点加入到队列最后。重复执行直到队列为空。
值得注意的是
- Bellmanford算法里最后return-1的判断条件写的是dist[n]>0x3f3f3f3f/2;而spfa算法写的是dist[n]==0x3f3f3f3f;其原因在于Bellmanford算法会遍历所有的边,因此不管是不是和源点连通的边它都会得到更新;但是SPFA算法不一样,它相当于采用了BFS,因此遍历到的结点都是与源点连通的,因此如果你要求的n和源点不连通,它不会得到更新,还是保持的0x3f3f3f3f。
- 由于 SPFA 算法是由 Bellman-ford 算法优化而来,在最坏的情况下时间复杂度和它一样即时间复杂度为 O(nm)O(nm),假如题目时间复杂度允许可以直接用 SPFA 算法去解 Dijkstra 算法的题目。
- Bellman_ford算法可以存在负权回路,是因为其循环的次数是有限制的因此最终不会发生死循环;但是SPFA算法不可以,由于用了队列来存储,只要发生了更新就会不断的入队,因此假如有负权回路请你不要用 SPFA 否则会死循环。
- 求负环一般使用 SPFA 算法,方法是用一个 cntcnt 数组记录每个点到源点的边数,一个点被更新一次就 +1+1,一旦有点的边数达到了 nn 那就证明存在了负环。
模板题:spfa求最短路 - TopsCoding
参考代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
typedef pair<int,int> PII;//到源点的距离,下标号
int dis[N];//各点到源点的距离
bool st[N];
int n,m;
vector<PII> g[N];
int spfa(){
queue<int> q;
memset(dis,0x3f,sizeof dis);
dis[1]=0;
q.push(1);
st[1]=true;
while(!q.empty()){
int t=q.front();
q.pop();
st[t]=false; // 从队列中取出来之后该节点 st 被标记为 false,代表之后该节点如果发生更新可再次入队
for(int i=0;i<g[t].size();i++){
int j=g[t][i].second, w = g[t][i].first;
if(dis[j]>dis[t]+w){
dis[j]=dis[t]+w;
if(!st[j]){ // 当前已经加入队列的结点,无需再次加入队列,即便发生了更新也只用更新数值即可,重复添加降低效率
st[j]=true;
q.push(j);
}
}
}
}
if(dis[n]==0x3f3f3f3f) return -1;
else return dis[n];
}
int main(){
ios::sync_with_stdio(0);
cin >> n >> m;
while(m--){
int a,b,c;
cin >> a >> b >> c;
g[a].push_back(make_pair(c, b));
}
int res=spfa();
if(res==-1) puts("impossible");
else cout << res;
return 0;
}
Copy
备注:关于 SPFA 为什么会被卡的解释,参考这里和这里2和这里3?
判断负环
求负环的常用方法,基于 SPFA,一般都用方法 2:
方法 1:统计每个点入队的次数,如果某个点入队 nn 次,则说明存在负环
方法 2:统计当前每个点的最短路中所包含的边数,如果某点的最短路所包含的边数大于等于 nn,则也说明存在环(鸽巢原理)


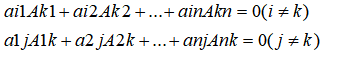



![[附源码]Python计算机毕业设计Django葡萄酒销售管理系统论文](https://img-blog.csdnimg.cn/79a2af6c50a94aca87912d83c1a4e317.png)

![[激光原理与应用-59]:激光器 - 光学 - 脉冲激光器的参数解析(能量、脉冲、周期、功率)](https://img-blog.csdnimg.cn/2eaa508d1ca64cd5a2279dd8e1700f07.png)