矩阵的行列式,determinate(简称det),是基于矩阵所包含的行列数据计算得到的一个标量。是为求解线性方程组而引入的。
1 行列式的定义
1.1 二阶行列式
对于二阶线性方程组
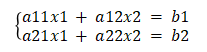
若b1b2都为0,则称齐次线性方程组,否则则称非齐次线性方程组
当如下情况时:
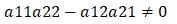
用消元法解得:
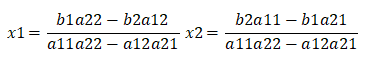
然后简化成如下公式:
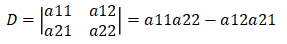
则解上面的二元线性方程组可得:
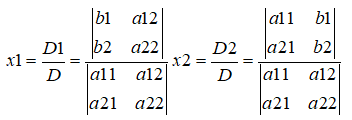
对于二阶和三阶行列式可用对角线法则。
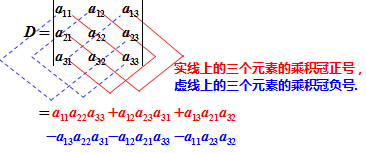
1.2 N阶行列式
从n个不同元素中任取m(m≤n)个元素,按照一定的顺序排列起来,叫做从n个不同元素中取出m个元素的一个排列。当m=n时所有的排列情况叫全排列。n阶排列共有n!个。
如1,2,3三个元素的全排列共6种,如下:
1,2,31,3,22,1,32,3,13,1,23,2,1
在一个排列中,如果一个较大的数排在了较小的数前面,就称这两个数构成一个逆序。一个排列逆序的总数称为该排列的逆序数。
用f(j1j2...jn)表示排列j1j2...jn的逆序数,例如f(31542)=5
3 之前有0个数比它大1 之前有1个数比它大5 之前有0个数比它大4 之前有1个数比它大2 之前有3个数比它大0+1+0+1+3=5
通过对二阶三阶行列式分析,可得二阶三阶和n阶的公式,如下:
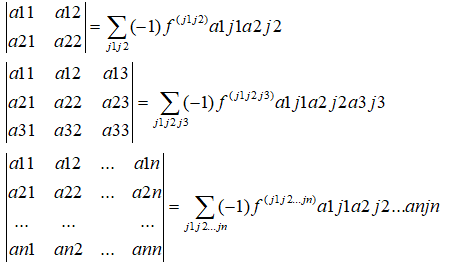
如下的例子计算:

2 行列式的性质
用定义计算行列式的值是很困难的,一般都利用行列式的性质简化行列式为上(下)三角形行列式后再计算。
规定如下行列式变换符号:
-
行列式i行(列)与j行(列)交换,记为ri↔rj(ci↔cj)
-
行列式的第i行(列)乘以常数c,记为cri(cci)
-
行列式的第j行(列)的k倍加到第i行(列),记为ri+krj(ci+kcj)
性质1:行列式行列互换,其值不变
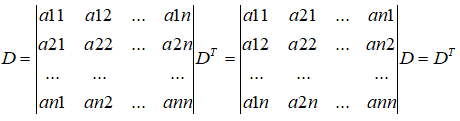
性质2:把行列式的任一行(列)所有元素乘以一个数k,等于用数k乘以这个行列式
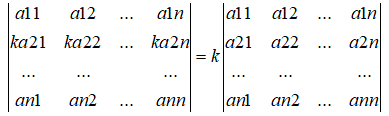
性质3:如果行列式的某一行(列)的每个元素都为0,则改行列式值为0
性质4:如果行列式的某一行(列)的每个元素都是两个元素的和,则等于两个行列式的和
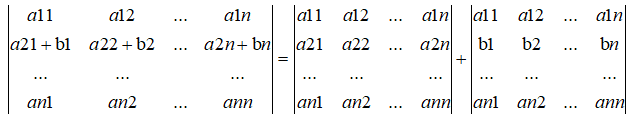
性质5:交换一个行列式的某两行(列),行列式的值异号
性质6:交换一个行列式的有两行(列)完全相同或成比例,则该行列式的值为零
性质7:把行列式的某一行(列)的倍数加到另一行(列)上,行列式的值不变
下图是一个简化例子:

3 代数余子式
在n阶行列式D中,划去元素aij所在的行与列,剩下的元素按原来的顺序构成n-1阶行列式,称为元素aij的余子式,为Mij。有记Aij=(-1)^(i+j)Mij,Aij称为元素aij的代数余子式。
代数余子式主要是用来将高阶行列式化为低阶行列式。
如下图的代数余子式:
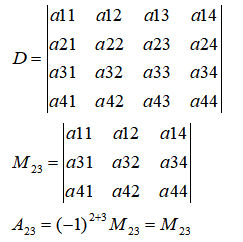
性质1:如第i行除了aij不为0其他都为0,则行列式的值如下:
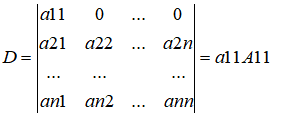
性质2:n阶行列式D等于它的任意一行(列)的各元素与其对应的代数余子式乘积之和,如下:
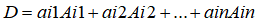
性质3:n阶行列式D某一行(列)的各元素与另一行(列)对应的元素的代数余子式乘积之和等于0,如下:
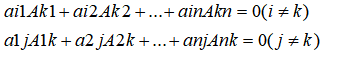



![[附源码]Python计算机毕业设计Django葡萄酒销售管理系统论文](https://img-blog.csdnimg.cn/79a2af6c50a94aca87912d83c1a4e317.png)

![[激光原理与应用-59]:激光器 - 光学 - 脉冲激光器的参数解析(能量、脉冲、周期、功率)](https://img-blog.csdnimg.cn/2eaa508d1ca64cd5a2279dd8e1700f07.png)