目录
分布
连续型变量的分布
正态分布
正态分布的推导
正态分布密度曲线
dnorm
正态分布的概率计算
正态分布累积曲线
总体分位数和尾概率
正态分布案例之一
R语言正态分布函数
正态分布相应的概率计算
正态分布的检验
shapiro.test()函数
Kolmogorov-Smirnov连续分布检验
KS的第二案例应用
总结
1.dnorm()函数
2.pnorm()函数
3.qnorm()函数
4.rnorm()函数
分布
表示分布最常用的方法是直方图(histogram),这种图用于展示各个值出现的频数或概率。频数指的是数据集中的一个值出现的次数。概率就是频数除以样本数量n。
用表示概率的直方图称为概率质量函数(Probability Mass Function, PMF)。这个函数是值到其概率的映射。
连续型变量的分布
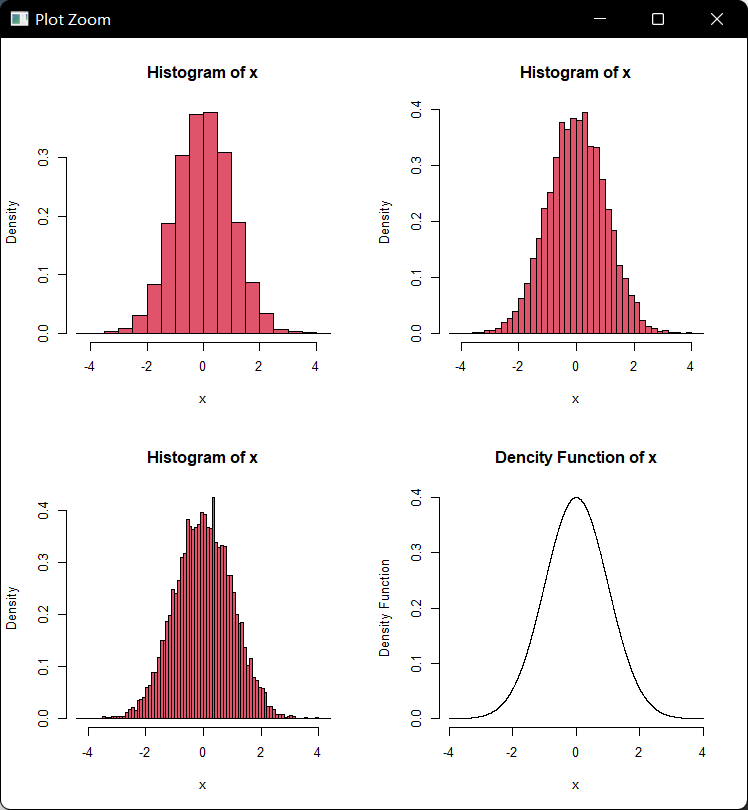
连续型变量是在连续区间取值,例如质量、长度、面积、体积、寿命、距离等就是连续型变量,现在试想一下连续变量观测值的直方图;如想其纵坐标为相对频数,那么所有这些矩形条的高度和为1,那么完全可以重新设置量纲,例这些矩形条的面积为1,如果不断增加观测值,并不断增加直方图的矩形条的数目,这些直方图就会越来越像一条光滑曲线,其下面的面积和为1,这种曲线就是概率密度函数(probability density function, pdf),简称为密度函数或密度,下图就展示了逐渐增加矩形条数的直方图和一个形状类型的密度曲线:
par(mfrow=c(2,2))
x=rnorm(10000)
z<-seq(-4,4,length=10000)
hist(x,20,probability=T,col=2)
hist(x,50,probability=T,col=2)
hist(x,100,probability=T,col=2)
plot(z,dnorm(z),type="l",
xlab="x",ylab="Density Function",
bty="n",
main="Dencity Function of x")
什么是密度?
这里说一下密度,密度是描述变量分布的一个重要概率,简单地说,它描述变量取各个值的可能性大小,变量在密度曲线高的位置取值的可能性比在低的位置取值的可能性大。在概率密度曲线中,纵坐标就是密度(Density)。
而密度曲线(density curve)是分布的一个数字模型,按照定义,任何密度曲线下的总面积都是1,在一个区间的密度曲线下的面积为出现在这个区间中的观测值占所有观测值的比例。
在矩形面积和为1的直方图中,连续变量落入某个矩阵的概率为该矩形的面积,类似地,连续变量落入一个区间的概率就是概率密度函数曲线在这个区间上所覆盖的面积,也就是密度函数在这个区间上的积分,根据初等微积分,连续函数在一个点的积分是0(因为曲线下面的面积退化成一条垂直于x轴,平行于y轴的直线),因此对于连续变量,取任何一个单独特定值的概率都是0,而只有变量取值于某个(或若干个)区间的概率才有可能大于0。连续变量和离散变量类似,它的密度函数(这时用f表示随机变量X的密度函数)必须满足f(x)≥0f(x)≥0,而且密度曲线下面覆盖的总面积为1,即:

而X落入区间(a,b)的概率则为:

连续变量也有累积分布函数(cumulative distribution function, CDF),定义为:

这样,和离散变量一样,如果要求P(a<X≦b)的值,就可以通过两个累积分布F(b)和F(a)之间在用公式获得,如下所示:
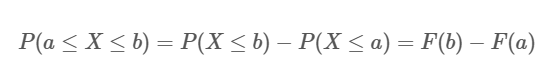
而不用根据密度函数求积分了。
连续随机变量也有描述变量“位置”的总体均数、总体中位数、总体百分位数以及描述变量分布(集中)程度的总体标准差和总体方差等概念,对于连续分布随机变量X,它的总体均值(通常用μ表示)定义为:
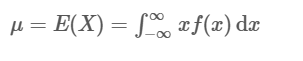
这也称为X的数学期望,变量X的总体方差(通常用δ2δ2表示),定义为:

总体标准差定义为总体方差的平方根,如下所示:

正态分布
下图是四个二项分布图,这四个二项分布有共同的p=0.1,但是有不同的n,分别为5,20,50,500,可以看出,当n较小时,分布很不对称,当n增加时,分布变得对称,实际上,当n充分大时,二项分布趋向于一个连续型对称分布,这就是正态分布(normal distribution),如下所示:
n<-c(5,20,50,500) p<-0.1 par(mfrow=c(2,2)) barplot(dbinom(0:n[1],n[1],p),main="Binomial(5,0.1)") barplot(dbinom(0:(2*floor(2*n[2]/5)),n[2],p),main="Binomial(20,0.1)") barplot(dbinom(0:(floor(n[3]/3)),n[3],p),main="Binomial(50,0.1)") barplot(dbinom(25:75,n[4],p),main="Binomial(500,0.1)")
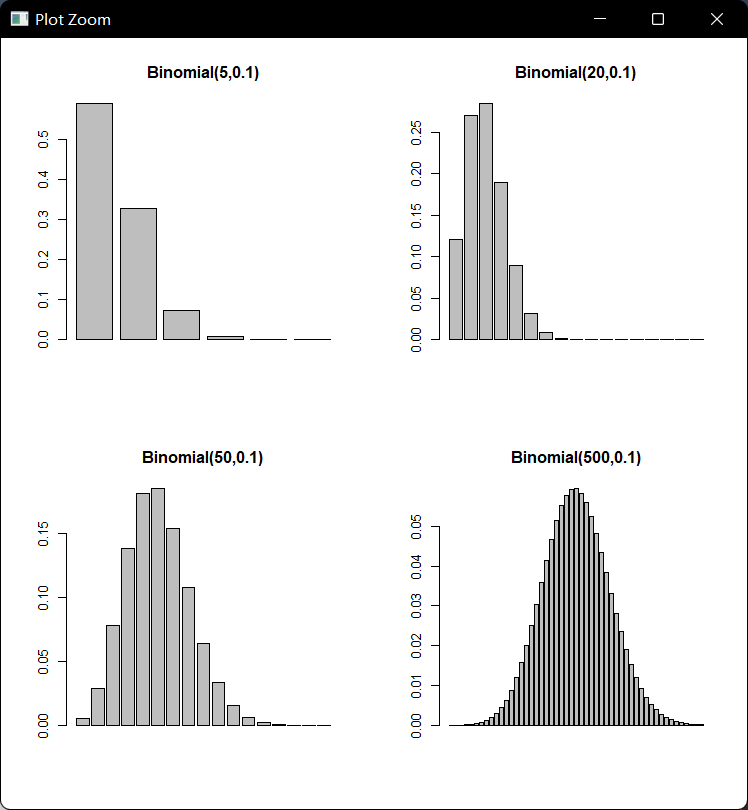
在实际生活中,近似地服从正态分布的变量也很常见,例如测量误差,商品的重量或尺寸,某特定人群的身高和体重等,此外,在一定条件下,许多不是正态分布的样本均值在样本量很大时,也可用正态分布来近似估计。
正态分布也是一族分布,不同的正态分布根据它们的均值和标准差不同而有所区别,因此一个正态分布用N(μ,δ)N(μ,δ)表示,其中μμ是总体均值,而δδ是总体标准差,正态分布也常用N(ν,δ2)N(ν,δ2)来表示,这里的δ2δ2为总体方差,这些总体参数在实际问题中是未知的,但可以估计,例如用样本均值和样本标准差来估计总体均值和总体标准差,正态分布的密度曲线是一个对称的钟形曲线(最高点在均值处)
正态分布的推导
在理解正态分布的时候,如果知道它的推导过程,以及曲线下面积是如何求的,就会对正态分布的理解更深入,但是这涉及到一定的数学知识,包括大数定量,微积分等,目前我没有能力理解这些,具体的可以看陈希孺的《概率论与数理统计》等资料。不过真正用这个函数来计算正态变量概率数值的情况不多,多数直接采用累积分布函数来计算的。
正态分布密度曲线
dnorm
在R中,dnorm()是正态分布的概率密度函数,d代表density,norm代表正态分布,返回给定x在标准正态分布下的概率密度。
对于一个给定的正态分布,X ∼ N(μ,σ2),μ代表均值,σ2代表方差,dnorm()可以计算给定x下的概率密度,即P(X<=x|μ=a,σ=b),比如,对于标准正态分布 X ∼ N(0,1),要计算x=1时的概率密度,即dnorm(1)=P(X<=1|μ=0,σ=1)
> dnorm(1) # 默认为标准正态分布,故亦可以写作下面这种形式 [1] 0.2419707 > dnorm(1,mean=0,sd=1) [1] 0.2419707
根据dnorm()的性质,我们可以利用dnorm()来绘制正态分布曲线
> x <- rnorm(100) > x [1] 0.067624027 0.446922747 -0.779610273 1.019910795 -0.611558691 -0.042208614 1.057542821 [8] 0.168769225 0.292759062 0.069769967 -1.884478653 0.210965341 0.487999663 0.079415785 [15] 0.547819110 1.218320307 -0.829277733 -0.180677502 -0.722302587 -0.275027962 1.147344053 [22] 0.057776822 0.620030502 -0.006237543 0.150433226 1.259527763 -0.828779833 -1.581627780 [29] -0.291715425 -0.275497338 -0.531884989 -0.022351625 -0.213368332 -0.661274484 1.052272355 [36] -1.491285952 -0.490500385 -0.289660378 -1.223280167 -0.407513962 -0.951917561 0.880820238 [43] 0.193889773 -1.401977549 -0.571268441 -0.680519505 -0.593670209 1.149960529 -0.366887812 [50] -1.401057013 0.520541718 -1.871404951 -1.529649961 0.380110232 -0.646800728 -1.745816661 [57] -1.658797701 -0.809181810 -1.228480576 -0.228532084 1.529535839 0.064914455 0.243817469 [64] 0.623980927 -1.621383762 -1.790768314 0.816892971 -0.278317894 -0.090169109 0.350612752 [71] 2.134799802 -0.105936765 -0.606534781 -1.037662539 -0.956454603 -1.271927292 -0.787623941 [78] -0.001952851 -0.906800210 2.335462375 -0.778546226 0.520102904 -1.076871213 2.310164950 [85] 0.001740659 -0.808784690 0.750435109 -0.453002059 2.304120907 0.192156923 0.659194960 [92] -0.807322096 -0.976952123 -0.392610629 -1.173103468 2.769663266 -0.085446868 2.340928468 [99] 0.309876876 -1.262045807 > x <- x[order(x)] > x [1] -1.884478653 -1.871404951 -1.790768314 -1.745816661 -1.658797701 -1.621383762 -1.581627780 [8] -1.529649961 -1.491285952 -1.401977549 -1.401057013 -1.271927292 -1.262045807 -1.228480576 [15] -1.223280167 -1.173103468 -1.076871213 -1.037662539 -0.976952123 -0.956454603 -0.951917561 [22] -0.906800210 -0.829277733 -0.828779833 -0.809181810 -0.808784690 -0.807322096 -0.787623941 [29] -0.779610273 -0.778546226 -0.722302587 -0.680519505 -0.661274484 -0.646800728 -0.611558691 [36] -0.606534781 -0.593670209 -0.571268441 -0.531884989 -0.490500385 -0.453002059 -0.407513962 [43] -0.392610629 -0.366887812 -0.291715425 -0.289660378 -0.278317894 -0.275497338 -0.275027962 [50] -0.228532084 -0.213368332 -0.180677502 -0.105936765 -0.090169109 -0.085446868 -0.042208614 [57] -0.022351625 -0.006237543 -0.001952851 0.001740659 0.057776822 0.064914455 0.067624027 [64] 0.069769967 0.079415785 0.150433226 0.168769225 0.192156923 0.193889773 0.210965341 [71] 0.243817469 0.292759062 0.309876876 0.350612752 0.380110232 0.446922747 0.487999663 [78] 0.520102904 0.520541718 0.547819110 0.620030502 0.623980927 0.659194960 0.750435109 [85] 0.816892971 0.880820238 1.019910795 1.052272355 1.057542821 1.147344053 1.149960529 [92] 1.218320307 1.259527763 1.529535839 2.134799802 2.304120907 2.310164950 2.335462375 [99] 2.340928468 2.769663266 > y <- dnorm(x) > y [1] 0.06757154 0.06925106 0.08026962 0.08691050 0.10078725 0.10716547 0.11421053 0.12382908 0.13121666 [10] 0.14931322 0.14950598 0.17766810 0.17990644 0.18758545 0.18878514 0.20048328 0.22340604 0.23286176 [19] 0.24754664 0.25250071 0.25359620 0.26445562 0.28286393 0.28298071 0.28755931 0.28765171 0.28799187 [28] 0.29255158 0.29439449 0.29463863 0.30734049 0.31648104 0.32059376 0.32364303 0.33089951 0.33191354 [37] 0.33448585 0.33887894 0.34632094 0.35372559 0.36003862 0.36715457 0.36935018 0.37297575 0.38232376 [46] 0.38255222 0.38378647 0.38408633 0.38413596 0.38865936 0.38996373 0.39248353 0.39670996 0.39732378 [55] 0.39748856 0.39858707 0.39884264 0.39893452 0.39894152 0.39894168 0.39827697 0.39810262 0.39803114 [64] 0.39797247 0.39768622 0.39445366 0.39330100 0.39164452 0.39151355 0.39016259 0.38725882 0.38220718 [73] 0.38024086 0.37515981 0.37113833 0.36102484 0.35415863 0.34847386 0.34839431 0.34335464 0.32917774 [82] 0.32836988 0.32103423 0.30103915 0.28576211 0.27066844 0.23715353 0.22933371 0.22806219 0.20656550 [91] 0.20594562 0.18993171 0.18047850 0.12385070 0.04085919 0.02805958 0.02767102 0.02609189 0.02576054 [100] 0.00861323 plot(x,y,type="l")
下面分别绘制均值(以下用m表示)为0,标准差(以下用sd表示)为1,m=0,sd=0.5,m=0,sd=2,m=-2,sd=1的正态分布密度曲线(密度曲线下面的积分面积对应的就是相应范围内的概率),可以看出不同的均值与标准差,正态分布的密度曲线形状就不一样:
set.seed(1000)
x <- seq(-5,5,length.out=100)
y <- dnorm(x,0,1)
plot(x,y,col="red",xlim=c(-5,5),ylim=c(0,1),type="l",
xaxs="i",yaxs="i",ylab="density",xlab="",
main="The Normal Density Distribution")
lines(x,dnorm(x,0,0.5),col="green")
lines(x,dnorm(x,0,2),col="blue")
lines(x,dnorm(x,-2,1),col="orange")
#legend("topright",legend=paste("m=",c(0,0,0,-2),"sd=",c(1,0.5,2,1)),lwd=1,col=c("red","green","blue","orange"))
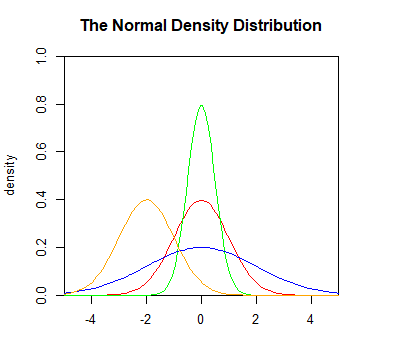
正态分布的概率计算
作为一个连续变量,正态变量落在某区间的概率不是等于在这个区间上,密度曲线下面的面积,下图的阴影面积等于标准正态分布变量落在区间(-1.5,1.5)中的概率,如果密度函数为ϕ(x)ϕ(x),那么这个面积就等于以下的积分,如下所示:

在计算机未广泛应用之前,为了方便计算,数学家们就编制了标准正态分布表,而在计算机广泛使用之后,则很容易计算出服从正态分布的数据的某个范围的概率,但为了理解正态分布的原理,还是先看一下如何使用标准正态分布表来计算一下标准正态分布变量落在区间(-1.5,1.5)中的概率。
在使用标准正态表之前,我们知道这些信息:
- 标准正态分布是关于y轴对称的;
- 标准正态分布的概率是落在-1.5到1.5这个区间内的曲线下面积;
现在查表,可以知道1.5对应的这个数值是0.9332,它表示小于1.5的曲线下面积是0.9332,-1.5没法查,但是可以查-1.5对称的曲线下面积,-1.5关于y轴对称的直线是0.5,它的曲线下面积为0.6915,也就是说小于0.5的曲线下面积为0.6915,那么大于0.5的曲线下面积为1-0.6915=0.3085,这个0.3085其实就是小于-1.5的曲线下面积,那么标准正态分布变量落在区间(-1.5,1.5)中的概率就是0.9332-0.3085=0.6247
也就是这下面的这个灰色面积,如下所示:
x<-c(seq(-4,4,length=1000)) y<-dnorm(x) r1<-0.5 r2<-1.5 x2<-c(r1,r1,x[x<r2&x>r1],r2,r2) y2<-c(0,dnorm(c(r1,x[x<r2&x>r1],r2)),0) plot(x,y,type="l",main="P(-0.5<Z<1.5)=0.6246553",xlab="z",ylab=expression(phi(z))) abline(0,0) polygon(x2,y2,col="grey")

不过,现在一般不用查表,使用软件计算即可,如下所示:
> pnorm(1.5)-pnorm(-0.5) [1] 0.6246553
正态分布累积曲线
代码如下所示:
set.seed(1000)
x <- seq(-5,5,length.out=100)
y <- pnorm(x,0,1)
plot(x,y,col="red",xlim=c(-5,5),ylim=c(0,1),type="l",
xaxs="i",yaxs="i",ylab="density",xlab="",
main="The Normal Cumulative Distribution")
lines(x,pnorm(x,0,0.5),col="green")
lines(x,pnorm(x,0,2),col="blue")
lines(x,pnorm(x,-2,1),col="orange")
legend("bottomright",legend=paste("m=",c(0,0,0,-2),"sd=",c(1,0.5,2,1)),lwd=2,cex=1,col=c("red","green","blue","orange"))

总体分位数和尾概率
对于连续型随机变量X,α下侧分位数(又称α分位数,α-quantile)定义为满足关系P(X≤x)=αP(X≤x)=α的数x,这里的α称为下(左)侧尾概率(lower/left tail probability)。
α上侧分位数(又称α上分位数,α-upper quantile)定义为它满足P(X≥x)=αP(X≥x)=α的数x,这里的α称为上(右)侧尾概率(upper/right tail probability)。
对于连续分布,α上侧分位数等于(1-α)下侧分位数,而(1-α)下侧分位数等于α上侧分位数,通常用zαzα表示标准正态分布α的上侧分位数,即对于标准正态分布变量Z,有P(Z>zα)=α,有些文献用符号Z(1−α)而不是Zα来表示α上侧分位数。
下图表示的就是标准正态分布0.05上侧分位数Zα=Z0.05(=1.645),图形右边在区间(Z0.05,+∞)曲线下的面积等于相应的尾概率(α=0.05):
x<-c(seq(-4,4,length=1000)) y<-dnorm(x) plot(x,y,type="l",xlab="z",ylab=expression(phi(z))) abline(0,0) r<-qnorm(0.05,low=F) polygon(c(r,r,x[x>r]),c(0,dnorm(c(r,x[x>r]))),col="red") text(0,0.2,expression(P(Z<z[0.05])==0.95)) text(2.5,0.08,expression(P(Z>z[0.05])==0.05)) text(1.5,0.02,expression(P(z[0.05])==1.645))

随后要介绍的χ2(卡方)分布,t分布和F分布都是由正态分布变量导出的三种分布。
正态分布案例之一
再看一个案例:
B县的全体高一学生参加某补习班的数学测验,计算分数后得知“数学测验结果”可视为平均值为45,标准差为10的正态分布,那么这些数据就可以表示为这个样子:
绘制出平均值为45,标准差为10的正态分布表示,下图斜线部分的面积是0.5,如下所示:
length(y)&length(x) x <- seq(0,90,by = .1) y <- dnorm(x,mean = 45,sd = 10) plot(x,y,type = "l") x1 <- seq(45,90,by=.1) y1 <- dnorm(x1,mean = 45,sd = 10) length(y1)&length(x1) polygon(c(45,x1,90),c(0,dnorm(x1,mean = 45,sd = 10),0),density = 12,angle = 45)
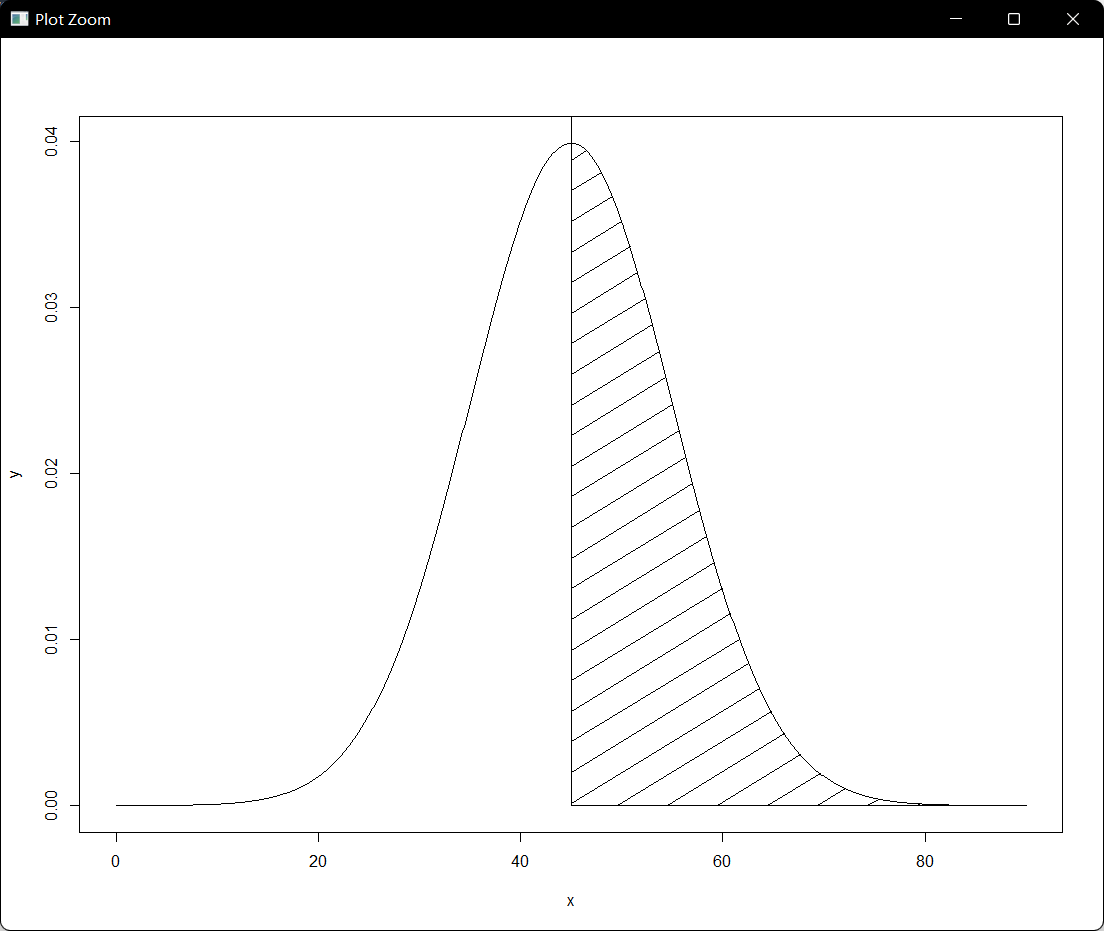
R语言正态分布函数
R语言中与正态分布有关的函数如下所示:
- 密度函数: dnorm(x, mean = 0, sd = 1, log = FALSE)
- 分布函数: pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
- 分位数函数:qnorm(p, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
- 随机函数: rnorm(n, mean = 0, sd = 1)
其余的分布函数与正态分布的前缀相同。
正态分布相应的概率计算
求正态N(3.1.5)变量X在区间(2,4)中的概率p,如下所示:
pnorm(4,3,1.5)-pnorm(2,3,1.5)
pnorm(4,3,1.5)-pnorm(2,3,1.5)
[1] 0.4950149
正态分布的检验
判断数据是否符合正态分布通常用的是非参数检验方法(因为总体分布未知)
shapiro.test()函数
Shapiro-Wilk正态分布检验: 用来检验是否数据符合正态分布,类似于线性回归的方法一样,是检验其于回归曲线的残差。该方法推荐在样本量很小的时候使用,样本在3到5000之间。该检验原假设为H0:数据集符合正态分布,统计量W 最大值是1,越接近1,表示样本与正态分布匹配。如果p-value小于显著性水平α(0.05),则拒绝H0,表示样本不符合正态分布,如果p-value在大于显著性水平,则接受H0,表示样本符合正态分布。
set.seed(1) s <- rnorm(1000) shapiro.test(s)
其结果为:
Shapiro-Wilk normality test
data: s
W = 0.9988, p-value = 0.7256
结论: W接近1,p-value>0.05,不能拒绝原假设,所以数据集s符合正态分布。
Kolmogorov-Smirnov连续分布检验
Kolmogorov-Smirnov连续分布检验:检验单一样本是不是服从某一预先假设的特定分布的方法。以样本数据的累计频数分布与特定理论分布比较,若两者间的差距很小,则推论该样本取自某特定分布族。
该检验原假设为H0:数据集符合正态分布,H1:样本所来自的总体分布不符合正态分布。令F0(x)表示预先假设的理论分布,Fn(x)表示随机样本的累计概率(频率)函数.
统计量D为: D=max|F0(x) - Fn(x)|,D值越小,越接近0,表示样本数据越接近正态分布,如果p-value小于显著性水平α(0.05),则拒绝H0。
Kolmogorov-Smirnov 检验,用法如下: ks.test(x, y, …, alternative = c(“two.sided”, “less”, “greater”), exact = NULL)
R语言中ks.test有四个参数,第一个参数x为观测值向量,第二个参数y为第二观测值向量或者累计分布函数或者一个真正的累积分布函数如pnorm,只对连续CDF有效。第三个参数为指明是单侧检验还是双侧检验,exact参数为NULL或者一个逻辑值,表明是否需要计算精确的P值。
set.seed(1) s <- rnorm(1000) ks.test(s,"pnorm")
结果如下:
One-sample Kolmogorov-Smirnov test
data: s
D = 0.0211, p-value = 0.7673
alternative hypothesis: two-sided
D值很小, p-value>0.05,不能拒绝原假设,所以数据集s符合正态分布。
KS的第二案例应用
比较两组数据的分布是否相同
ks.test(rnorm(100),rnorm(50))
Two-sample Kolmogorov-Smirnov test
data: rnorm(100) and rnorm(50)
D = 0.14, p-value = 0.5185
alternative hypothesis: two-sided
在这一案例中,我们比较了两个均值和方差一样的观测值,他们D值很小,p值大于0.05,所以我们不能拒绝两个观测值分布相同的假设。
KS比较某一数据符合某一分布
检验一组数据是否符合均匀分布(生成均匀分布的函数为runif)),如下所示:
ks.test(rnorm(100),"punif")
结果中p-value为2.2e-16,我们用rnorm(100)生成的是正态分布的数据,因此它不符合均匀分布(参数为punif)。如果参数设为pnorm,再看一下。
ks.test(rnorm(100),"pnorm")
结果的p值为0.6722,符合正态分布。
总结
在随机收集来自独立来源的数据中,通常观察到数据的分布是正常的。 这意味着,在绘制水平轴上的变量的值和垂直轴中的值的计数时,我们得到一个钟形曲线。 曲线的中心代表数据集的平均值。 在图中,百分之五十的值位于平均值的左侧,另外五十分之一位于图的右侧。 统称为正态分布。
R有四个内置函数来生成正态分布。它们在下面描述
dnorm(x, mean, sd) pnorm(x, mean, sd) qnorm(p, mean, sd) rnorm(n, mean, sd)
以下是上述函数中使用的参数的描述
- x - 是数字的向量。
- p - 是概率向量。
- n - 是观察次数(样本量)。
- mean - 是样本数据的平均值,默认值为零。
- sd - 是标准偏差,默认值为1。
1.dnorm()函数
该函数给出给定平均值和标准偏差在每个点的概率分布的高度。
setwd("F:/worksp/R")
# Create a sequence of numbers between -10 and 10 incrementing by 0.1.
x <- seq(-10, 10, by = .1)
# Choose the mean as 2.5 and standard deviation as 0.5.
y <- dnorm(x, mean = 2.5, sd = 0.5)
# Give the chart file a name.
png(file = "dnorm.png")
plot(x,y)
# Save the file.
dev.off()
结果如下:👇
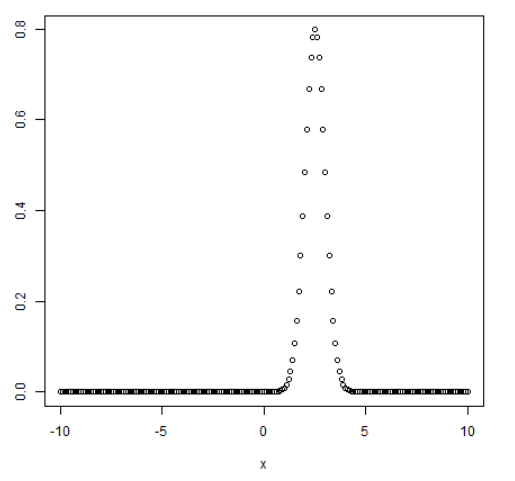
2.pnorm()函数
该函数给出正态分布随机数小于给定数值的概率。它也被称为“累积分布函数”。
setwd("F:/worksp/R")
# Create a sequence of numbers between -10 and 10 incrementing by 0.2.
x <- seq(-10,10,by = .2)
# Choose the mean as 2.5 and standard deviation as 2.
y <- pnorm(x, mean = 2.5, sd = 2)
# Give the chart file a name.
png(file = "pnorm.png")
# Plot the graph.
plot(x,y)
# Save the file.
dev.off()
结果运行如下

3.qnorm()函数
该函数采用概率值,并给出其累积值与概率值匹配的数字值。
setwd("F:/worksp/R")
# Create a sequence of probability values incrementing by 0.02.
x <- seq(0, 1, by = 0.02)
# Choose the mean as 2 and standard deviation as 3.
y <- qnorm(x, mean = 2, sd = 1)
# Give the chart file a name.
png(file = "qnorm.png")
# Plot the graph.
plot(x,y)
# Save the file.
dev.off()

4.rnorm()函数
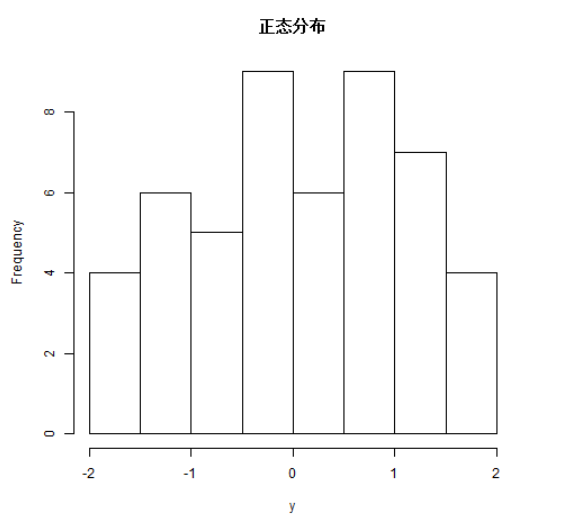
该函数用于生成分布正常的随机数,它将样本大小作为输入,并生成许多随机数。我们绘制直方图以显示生成数字的分布。
setwd("F:/worksp/R")
# Create a sample of 50 numbers which are normally distributed.
y <- rnorm(50)
# Give the chart file a name.
png(file = "rnorm.png")
# Plot the histogram for this sample.
hist(y, main = "正态分布")
# Save the file.
dev.off()



![[附源码]Node.js计算机毕业设计高校运动会管理系统 Express](https://img-blog.csdnimg.cn/80c3f98c31814de88822f7436c3a2ef6.png)