Problem - E - Codeforces
题意：

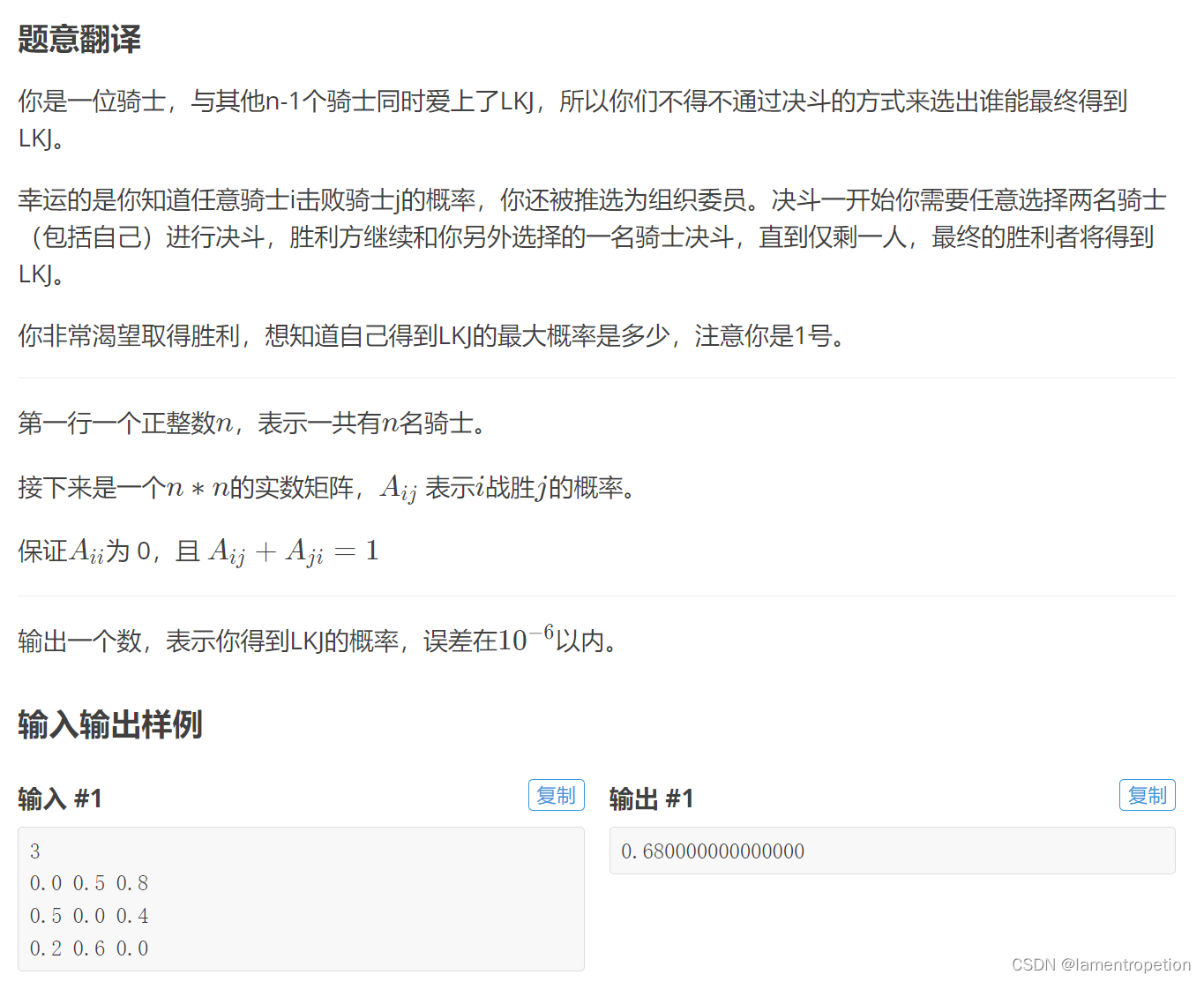
思路：

首先，n <= 18，应当想到状压

很明显，这里可以使用状压DP

设 dp[s][i] 表示，现在选的方案为 s ，且我是 i 的最终胜利的概率是多少

重要的是转移

这是很经典的状压DP转移方式：选择两个1，然后转移

有两种情况，j 战胜 k 或 k 战胜 j 

根据这两种情况乘一下概率即可

概率DP就是看当前状态从哪些状态转移过来，边权就是概率，加一下就好了

然后答案就是枚举一下我是哪个就好了

一切都是典中典

Code：

#include <bits/stdc++.h>

#define int long long

using i64 = long long;

constexpr int N = 1e2 + 10;
constexpr int M = 1e2 + 10;
constexpr int P = 2e2 + 10;
constexpr i64 Inf = 1e18;
constexpr int mod = 1e9 + 7;
constexpr double eps = 1e-6;

int n;
double p[20][20];
double dp[(1 << 19)][20];

void solve() {
    std::cin >> n;
    for (int i = 0; i < n; i ++) {
        for (int j = 0; j < n; j ++) {
            std::cin >> p[i][j];
        }
    }

    if (n == 1) {
        std::cout << std::fixed << std::setprecision(8) << 1.0 << "\n";
        return;
    }
    
    dp[1][0] = 1.0;

    for (int s = 0; s < (1 << n); s ++) {
        for (int j = 0; j < n; j ++) {
            if (((s >> j) & 1) == 0) continue;
            for (int k = 0; k < n; k ++) {
                if (((s >> k) & 1) == 0) continue;
                dp[s][j] = std::max(dp[s][j], p[j][k] * dp[s - (1 << k)][j] + p[k][j] * dp[s - (1 << j)][k]); 
            }
        }
    }

    double ans = 0;
    for (int j = 0; j < n; j ++) {
        ans = std::max(ans, dp[(1 << n) - 1][j]);
    }

    std::cout << std::fixed << std::setprecision(8) << ans << "\n";
}
signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    
    int t = 1;

    while (t--) {
        solve();
    }
    
    return 0;
}