参考：

kenjihiranabe——The-Art-of-Linear-Algebra-zh-CN

详细计算方法与理论：见 矩阵论

线性代数的本质在于将具体事物抽象为数学对象，并描述其静态和动态特性

• 最基本的概念是 set

  集合的定义是由某些具有某些共性的对象汇总成的集体。

  将这些对象用数字或符号表示(对象映射到数域)，这样集合中的元素就变为了多个数字或符号以某种方式排列成的组合

• 向量实质上是n维线性空间中的静止点
• 线性变换描述了向量或者作为参考系的坐标系变化，可以用矩阵表示
• 矩阵的特征值和特征向量描述了变化的速度与方向

【AI】数学基础——线代（矩阵&特征值,特征向量&矩阵分解）

2.1 对象的表示

在线代中，由单独的数a构成的元素被称为 标量 (scalar)：一个标量可以是整数、实数或复数

• $a,b,c$

多个标量 $a_1,a_2,\cdots ,a_n$ 按一定顺序组成一个序列，这样的元素称为 向量 (vector)

• 向量代表了维度的增加，向量中每个元素需要使用一个索引确定
• $\alpha =(a_1,a_2,\cdots ,a_n)$

矩阵 (matrix) 由维度相同的向量组成

• 矩阵代表了维度的增加，矩阵中每个元素需要使用两个索引确定
• $A=\left(\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right)$

张量 (tensor) 矩阵中的每个元素都是向量，则形成张量

• $A=\left(\begin{array}{cccc}1& 1& 2& 2\\ 0& 1& 0& 2\\ 3& 3& 2& 2\\ 0& 3& 0& 2\end{array}\right)=\left(\begin{array}{cc}1& 2\\ 3& 2\end{array}\right)\otimes \left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right)$

---

计算机处理离散取值的二进制信息，因此模拟世界的信号必须在定义域和值域上同时进行数字化，才能被计算机存储和处理。

线性代数是用模拟数字世界表示真实物理世界的工具

在计算机存储中：

• 标量 占据零维度数组

• 向量 占据一维数组：如语音信号

• 矩阵 占据二维数组：如灰度图像

• 张量 占据三维乃至更高维度数组：如RGB图像和视频

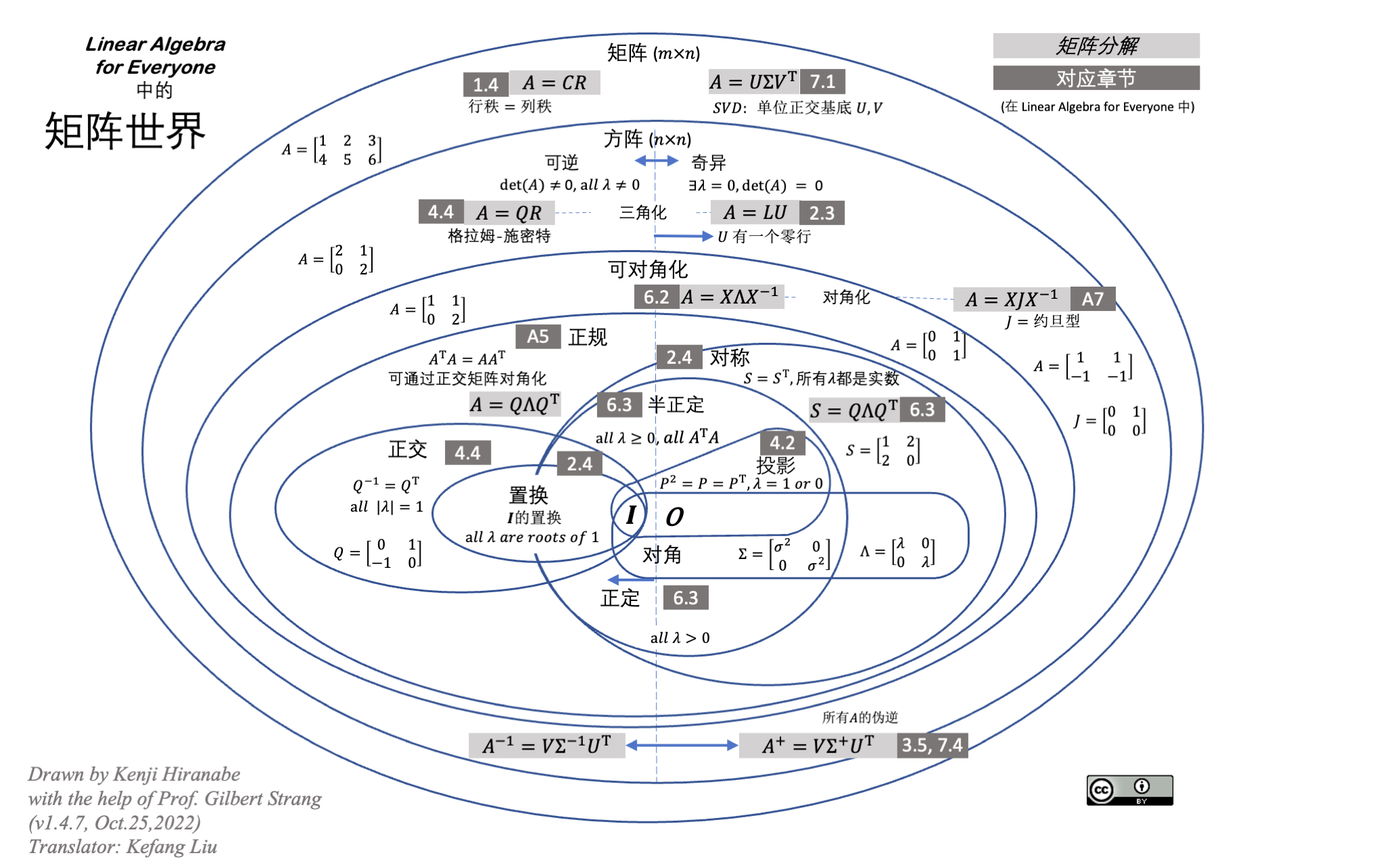
  ${\vec{e}}^T\otimes \vec{e}=\left({\vec{i}}^T,{\vec{j}}^T,{\vec{k}}^T\right)\left(\begin{array}{r}\vec{i}\\ \vec{j}\\ \vec{k}\end{array}\right)=\left(\begin{array}{ccc}{\vec{i}}^T\cdot \vec{i}& {\vec{j}}^T\cdot \vec{i}& {\vec{k}}^T\cdot \vec{i}\\ {\vec{i}}^T\cdot \vec{j}& {\vec{j}}^T\cdot \vec{j}& {\vec{k}}^T\cdot \vec{j}\\ {\vec{i}}^T\cdot \vec{k}& {\vec{j}}^T\cdot \vec{k}& {\vec{k}}^T\cdot \vec{k}\end{array}\right)=\left(\begin{array}{ccc}(\vec{i},\vec{i})& (\vec{i},\vec{j})& (\vec{i},\vec{k})\\ (\vec{j},\vec{i})& (\vec{j},\vec{j})& (\vec{j},\vec{k})\\ (\vec{k},\vec{i})& (\vec{k},\vec{j})& (\vec{k},\vec{k})\end{array}\right)=\left(\begin{array}{ccc}{\sigma }_{11}& {\sigma }_{12}& {\sigma }_{13}\\ {\sigma }_{21}& {\sigma }_{22}& {\sigma }_{23}\\ {\sigma }_{31}& {\sigma }_{32}& {\sigma }_{33}\end{array}\right)$

  描述空间中各点沿各方向的受力情况

  

2.2 线性空间

2.2.1 向量

$\vec{m}=m_x\vec{i}+m_y\vec{j}+m_z\vec{k}=(m_x,m_y,m_z)\left(\begin{array}{r}\vec{i}\\ \vec{j}\\ \vec{k}\end{array}\right)$

• 大小
• 方向

2.2.2 向量空间

如果有一个集合，它的元素都是具有相同维数的向量

• 定义了加法和数乘等结构化运算，将这个空间称为 线性空间

• 定义了内积运算的线性空间，将这个空间称为 内积空间

在线性空间中，任一一个向量代表的是n维空间中的一个点；线性空间中的任一点也都可以唯一地用一个向量表示

• 0维：原点

  0维圆

  

• 1维：坐标轴

  1维圆

  

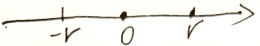
• 2维：平面

  2维圆：用线截为1维圆

  

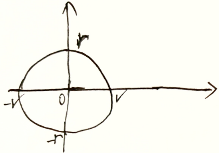
• 3维：空间

  3维球：用平面截为2维圆

  

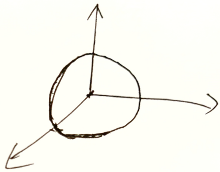
线性空间参考系

正交基 ：一组两两正交的向量构成了这个空间的正交基

标准正交基 ：（欧几里得空间）正交基中基向量的 $L^2$ 范数的单位长度为1，则这组正交基就是标准正交基

• 正交基的作用就是给内积空间定义基准，用于空间中的所有向量（点）

2.2.3 范数(模)

用于描述向量大小，记为 $\Vert \cdot \Vert$

可以理解为：将向量转换为实数的函数

性质

• 任一向量 $\vec{X}$ ，$\Vert X\Vert \ge 0$ ，当且仅当 $\vec{X}=\vec{0}$ ，有 $\Vert X\Vert =0$
• $\Vert \lambda X\Vert =\lambda \Vert X\Vert$
• 三角不等式：$\Vert X+Y\Vert \le \Vert X\Vert +\Vert Y\Vert$

几种范数

L-0范数

$\Vert X{\Vert }_0=向量分量非零元素个数$

• $\Vert \left(\begin{array}{r}1\\ 0\end{array}\right){\Vert }_0=1$ ，$\Vert \left(\begin{array}{r}1\\ 2\end{array}\right){\Vert }_0=2$

L-1范数(最大列和)

$\Vert X{\Vert }_1={\sum }_{i=1}^n|x_i|$

L-2范数

$\Vert X{\Vert }_2=\sqrt{{\sum }_{i=1}^n|x_i{|}^2}$

L-p范数

$\Vert X{\Vert }_p=\sqrt[p]{{\sum }_{i=1}^n|x_i{|}^2}$

L-$\infty$范数(最大行和)

∥ X ∥ ∞ = max ⁡ 1 ≤ i ≤ n { ∣ x i ∣ } \Vert X\Vert_\infty=\max_{1\le i\le n}\{\vert x_i\vert\} ∥X∥∞​=max1≤i≤n​{∣xi​∣}

p范数与无穷范数关系

L-p范数
令 ∣ x j ∣ = max ⁡ 1 ≤ i ≤ n { ∣ x i ∣ } ⇒ ∣ x j ∣ ∞ ≫ ∣ x i ∣ ∞ ∥ X ∥ p = ∑ i = 1 n ∣ x i ∣ p p = p → ∞ ∣ x 1 ∣ ∞ + ∣ x 2 ∣ ∞ + ⋯ + ∣ x n ∣ ∞ ∞ ≈ ∣ x j ∣ ∞ ∞ = ∣ x j ∣ = max ⁡ 1 ≤ i ≤ n { ∣ x i ∣ } \begin{aligned} &令 \vert x_j\vert=\max_{1\le i\le n}\{\vert x_i\vert\} \Rightarrow \vert x_j\vert^{\infty}\gg \vert x_i\vert^{\infty}\\ &\Vert X\Vert_p=\sqrt[p]{\sum_{i=1}^n\vert x_i\vert^p}\xlongequal{p\rightarrow \infty}\sqrt[\infty]{\vert x_1\vert^{\infty}+\vert x_2\vert^{\infty}+\cdots+\vert x_n\vert^{\infty}}\approx{} \sqrt[\infty]{\vert x_j\vert^\infty}=\vert x_j\vert=\max_{1\le i\le n}\{\vert x_i\vert\} \end{aligned} ​令∣xj​∣=1≤i≤nmax​{∣xi​∣}⇒∣xj​∣∞≫∣xi​∣∞∥X∥p​=pi=1∑n​∣xi​∣p ​p→∞ ∞∣x1​∣∞+∣x2​∣∞+⋯+∣xn​∣∞ ​≈∞∣xj​∣∞ ​=∣xj​∣=1≤i≤nmax​{∣xi​∣}​

距离

欧氏距离（L-2范数）：$L-2(A,B)=\sqrt{m_x^2+m_y^2}$

曼哈顿距离（L-1范数）： $L-1(A,B)=|m_x|+|m_y|$

2.2.4 向量运算

模——向量的大小

$n$ 维向量的模长，$|X|=\sqrt{(X,X)}=\sqrt{x_1^2+x_2^2+\cdots +x_n^2}\ge 0$

单位向量 $|x|=1$

齐次性 $|\lambda x|=|\lambda |\cdot |x|$

三角不等性 $|x+y|\le |x|+|y|$

内积——向量间的相对位置

$矢量\to 标量$

$x=\left(\begin{array}{r}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right)$ ，$y=\left(\begin{array}{r}{y}_1\\ y_2\\ ⋮\\ y_n\end{array}\right)$

$(x,y)=y^{T}x=y_1{x}_1+y_2{x}_2+\cdots +y_n{x}_n$

$(y,x)=x^{T}y=x_1{y}_1+x_2{y}_2+\cdots +x_n{y}_n$

性质

• 对称性：对于实数向量内积 $(x,y)=(y,x)$

• 线性

  $(x,\lambda y)=(\lambda x,y)=\lambda (x,y)$

  $(x+y,z)=(x,z)+(y,z)$

内积描述的是夹角，用于表示两个向量之间的相对位置

$A\cdot B=\Vert A\Vert \cdot \Vert B\Vert cos\theta$

若 $A\perp B$ ，则 $\theta =\frac{\pi }{2}$ ，$A\cdot B=0$

投影

若 $\Vert B\Vert =1$ ，则 $A\cdot B$ 为A在B上的投影长度

向量乘向量

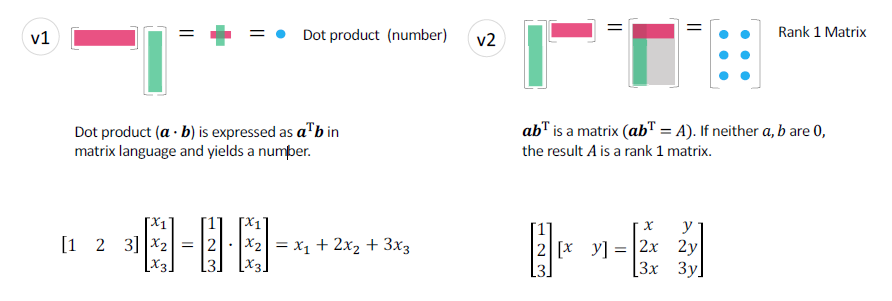
向量内积与秩1矩阵

2.2.5 正交向量组与规范正交基

$(x,y)=0$ ，则两向量正交

正交向量组

两两正交的非零向量组

• 正交向量组必线性无关

eg

已知 $R^3$ 空间 ${\alpha }_1=\left(\begin{array}{r}1\\ 1\\ 1\end{array}\right)$ ，${\alpha }_2=\left(\begin{array}{r}1\\ -2\\ 1\end{array}\right)$ 正交，求 ${\alpha }_3$ 使 ${\alpha }_1,{\alpha }_2,{\alpha }_3$ 为正交向量组

设 ${\alpha }_3=\left(\begin{array}{r}{x}_1\\ x_2\\ x_3\end{array}\right)$ ，由于 ${\alpha }_1,{\alpha }_2,{\alpha }_3$ 两两正交 ，有 $({\alpha }_1,{\alpha }_3)=({\alpha }_2,{\alpha }_3)=0\Rightarrow \{\begin{array}{rl}& x_1+x_2+x_3=0\\ & x_1-2x_2+x_3=0\end{array}$

有 $AX=\left(\begin{array}{ccc}1& 1& 1\\ 1& -2& 1\end{array}\right)\left(\begin{array}{r}{x}_1\\ x_2\\ x_3\end{array}\right)=0$ ，$A\to \left(\begin{array}{ccc}1& 1& 1\\ 1& -2& 1\end{array}\right)\to \left(\begin{array}{ccc}1& 1& 1\\ 0& -3& 0\end{array}\right)\to \left(\begin{array}{ccc}1& 0& 1\\ 0& 1& 0\end{array}\right)$

$r(A)=2,n-r(A)=1$ ，故线性方程组的基础解系中有一个无关向量

$\therefore \{\begin{array}{rl}& x_1=-x_3\\ & x_2=0\end{array}\Rightarrow {\alpha }_3=\left(\begin{array}{r}-1\\ 0\\ 1\end{array}\right)$

---

规范正交基

$n$ 维向量 $e_1,e_2\cdots ,e_r$ 是向量空间 $V\subset R^n$ 中的向量
$$\{\begin{array}{rl}& e_1,e_2\cdots ,e_r为单位正交向量\\ & e_1,e_2\cdots ,e_r是V的一个基\end{array}$$
则称 $e_1,e_2\cdots ,e_r$ 为 $V$ 的一个规范正交基

如：

$e_1=\left(\begin{array}{r}1\\ 0\\ 0\\ 0\end{array}\right),e_2=\left(\begin{array}{r}0\\ 1\\ 0\\ 0\end{array}\right),e_3=\left(\begin{array}{r}0\\ 0\\ 1\\ 0\end{array}\right),e_4=\left(\begin{array}{r}0\\ 0\\ 0\\ 1\end{array}\right)$ 是 $R^4$ 的一个规范正交基

2.2.6 向量组的秩

设向量组 ${\alpha }_1,\cdots ,{\alpha }_n$ ，存在 ${\alpha }_1,\cdots ,{\alpha }_s$ ，使 ${\alpha }_j=k_1{\alpha }_1+\cdots +k_s{\alpha }_s(j\ne 1,2,\cdots ,s)$ ，则称 ${\alpha }_j$ 可由 ${\alpha }_s,\cdots ,{\alpha }_s$ 线性表出

线性无关 ：若有 $k_1{\alpha }_1+\cdots +k_r{\alpha }_r=0\Rightarrow k_1=k_2=\cdots =k_r=0$ ，则称 ${\alpha }_1,\cdots ,{\alpha }_r$ 为极大线性无关组

$r({\alpha }_1\cdots {\alpha }_n)=r({\alpha }_1\cdots {\alpha }_r)=r$ 为向量组的秩