【车载雷达信号处理】利用sinc函数实现扣点

news2024/10/7 16:25:05

针对信号处理流程中多次FFT输出的频谱结果，在特殊的场景下，可能存在针对某一特定频点的固定"虚警"，所以针对某一个特定频点进行“扣点”的操作是常有的信号处理流程需求。不仅如此，针对最大能量值的扣点也能在不适合使用cfar进行目标检测的情况下（诸如插入了大量的0从而进行的3DFFT），扣取当前FFT结果能量最大点，然后将它的能量分别与FFT扣点剩余的所有频点能量的均值乘以一个系数后进行比较，不断循环从而筛选出目标的角度信息。本文介绍了利用sinc函数对FFT结果进行扣点的操作。

目录

卷积

信号重建

利用sinc函数实现扣点

卷积

所谓两个函数的卷积，本质上就是先将一个函数翻转，然后进行滑动叠加。在连续情况下，叠加指的是对两个函数的乘积求积分，在离散情况下就是加权求和。多次滑动得到的一系列叠加值，最终构成卷积函数。下面我在网上看到的对卷积的一种通俗理解以及相关的例子：

  1. 从“积”的过程可以看到，我们得到的叠加值，是个全局的概念。以信号分析为例，卷积的结果是不仅跟当前时刻输入信号的响应值有关，也跟过去所有时刻输入信号的响应都有关系，考虑了对过去的所有输入的效果的累积。在图像处理的中，卷积处理的结果，其实就是把每个像素周边的，甚至是整个图像的像素都考虑进来，对当前像素进行某种加权处理。所以说，“积”是全局概念，或者说是一种“混合”，把两个函数在时间或者空间上进行混合。

  2. 进行“卷”（翻转）的目的其实是施加一种约束，它指定了在“积”的时候以什么为参照。在信号分析的场景，它指定了在哪个特定时间点的前后进行“积”，在空间分析的场景，它指定了在哪个位置的周边进行累积处理。

下面对卷积这种操作从信号分析的角度举个例子：

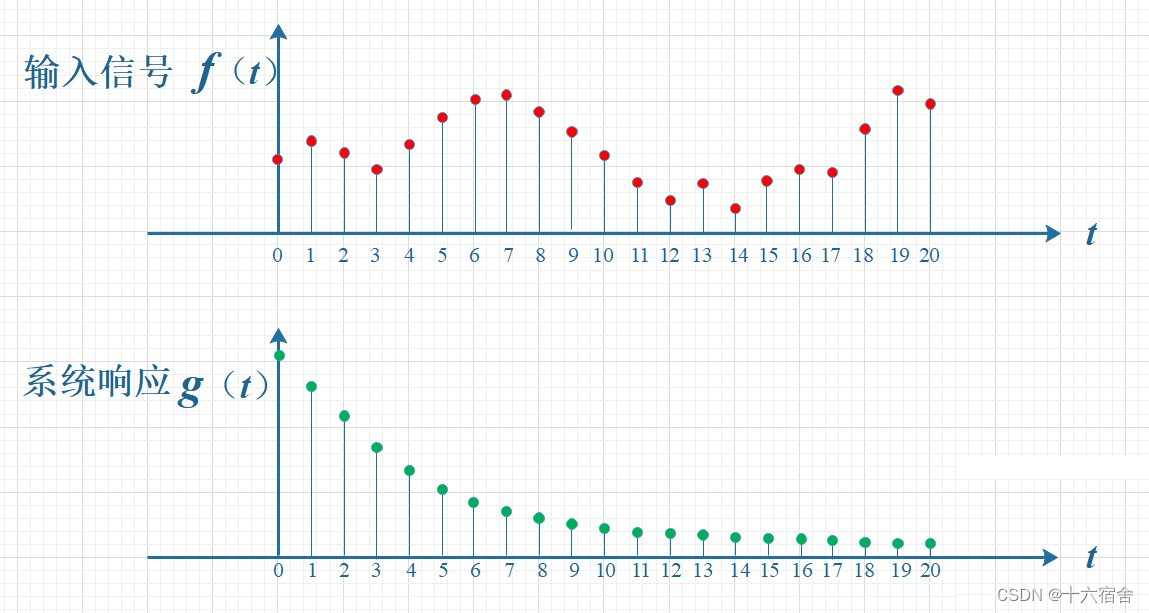
如下图所示，输入信号是 f(t) ，是随时间变化的。系统响应函数是 g(t) ，图中的响应函数是随时间指数下降的，它的物理意义是说：如果在 t=0 的时刻有一个输入，那么随着时间的流逝，这个输入将不断衰减。换言之，到了 t=T时刻，原来在 t=0 时刻的输入f(0)的值将衰减为f(0)g(T)。

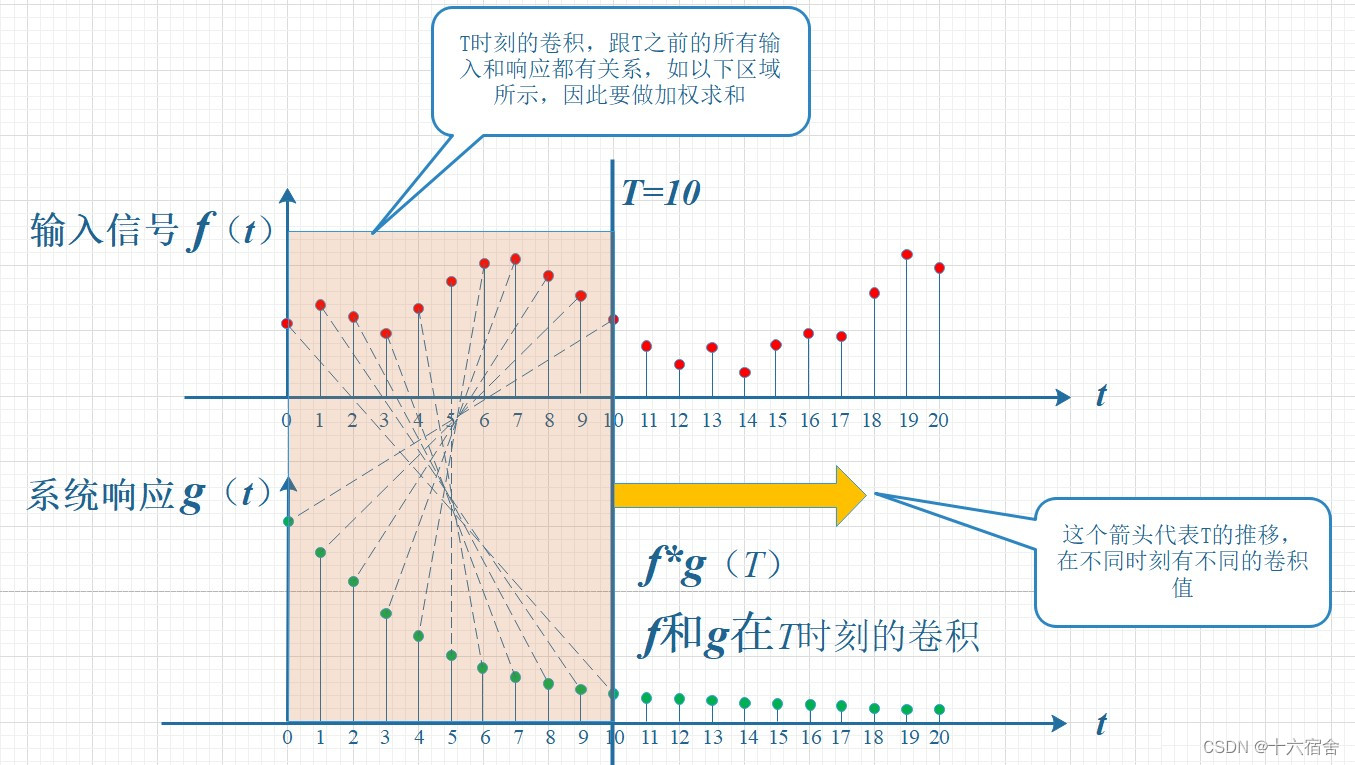
考虑到信号是连续输入的，也就是说，每个时刻都有新的信号进来，所以，最终输出的是所有之前输入信号的累积效果。如下图所示，在T=10时刻，输出结果跟图中带标记的区域整体有关。其中，f(10)因为是刚输入的，所以其输出结果应该是f(10)g(0)，而时刻t=9的输入f(9)，只经过了1个时间单位的衰减，所以产生的输出应该是 f(9)g(1)，如此类推，即图中虚线所描述的关系。这些对应点相乘然后累加，就是T=10时刻的输出信号值，这个结果也是f和g两个函数在T=10时刻的卷积值。

信号重建

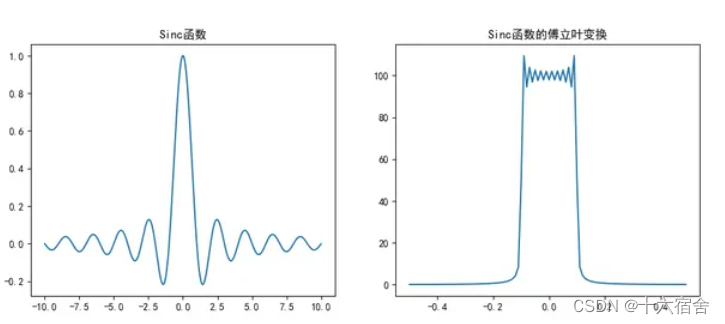
将模拟信号转换为数字信号的过程，在信号处理领域叫做采样(Sampling)。我们可以形象地把这个过程理解为使用一连串宽度非常窄的脉冲和输入信号相乘。而得到的结果则是一连串时间上不连续的脉冲。我们在信号重建的时候，只需要在频谱上做一个低通滤波，把那些因为对时域信号采样引起的频域周期延展出来的频率过滤掉，得到的就是原始的信号。而根据傅立叶变换的性质，在频域上乘积，等价于在时域上的卷积。而低通滤波器，可以近似看为一个矩形函数。Sinc函数的傅立叶变换，正好近似矩形函数。

下面的matlab代码实现了利用sinc函数恢复信号的过程，读者可以调整参数体会整个插值恢复信号的过程。

%参数设定
T = 2;
f1 = 5;
f2 = 10;
fs = 40;
%可得参数
N = T * fs;
t = linspace(-T/2, T/2, 100*N);
f_ori = 0.5 * cos(2 * pi * f1 * t) - sin(2 * pi * f2 * t) + 1;
figure(1);
plot(t, f_ori);xlim([-T/10, T/10]);title('原始信号');
%采样
t2 = linspace(-T/2, T/2, N);
f_sam = 0.5 * cos(2 * pi * f1 * t2) - sin(2 * pi * f2 * t2) + 1;
figure(2);
stem(t2, f_sam);xlim([-T/10, T/10]);title('采样信号');
%恢复
y = [];
for i = 1 : length(t)
    x = t(i);
    h = sinc((x - t2).*fs);
    g = dot(f_sam, h);
    y = [y,g];
end
figure(3);
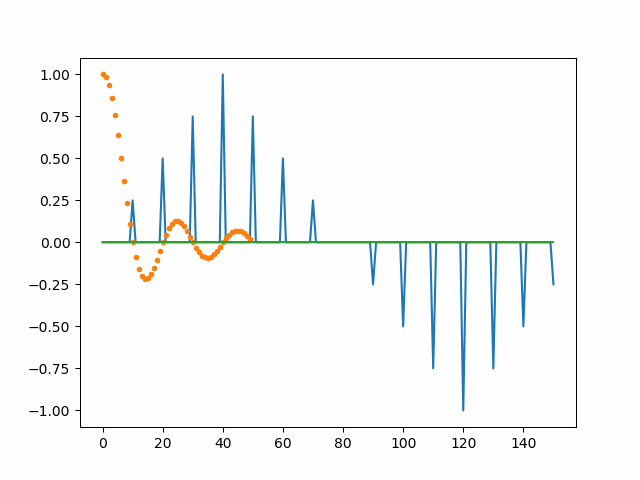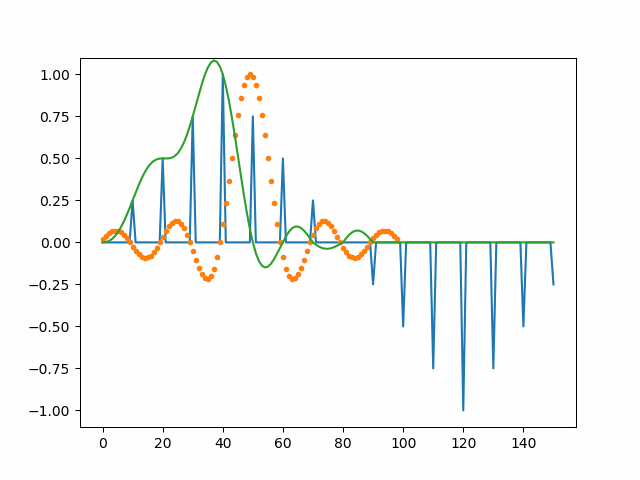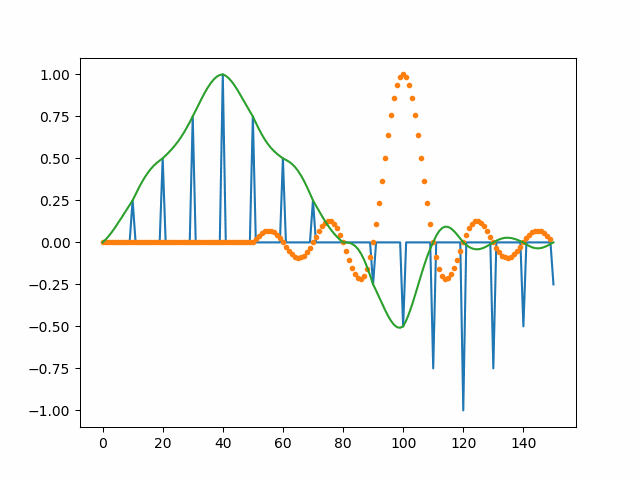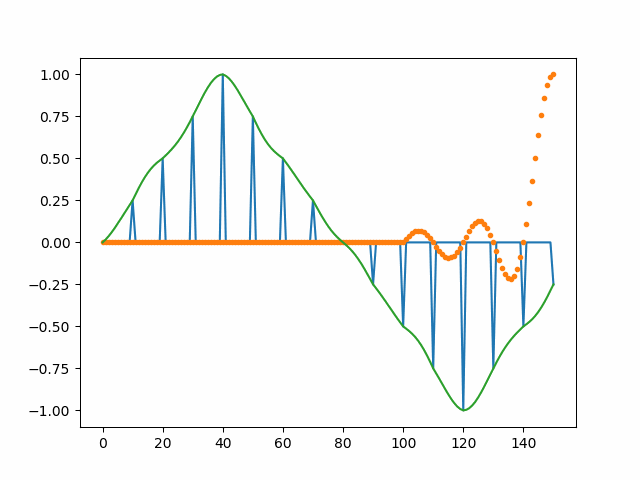
plot(t, y);xlim([-T/10, T/10]);title('恢复信号');

下面的图展示了采样信号与sinc函数卷积获得原始信号的过程，供读者对整个的恢复过程有一个直观的印象。

利用sinc函数实现扣点

扣点可以理解成插值的逆操作，我们不仅需要把我们想扣的点置0，还需要将这个点对其余点的影响消除。我们以对FFT的结果将能量最大的点进行扣选，主要的步骤如下：

  1. 将FFT的结果中对应的abs值中最大点的位置（下标）和他的频率值（复数）保存。
  2. 根据获取的位置移动sinc函数数组，然后乘以它的频率值，获得与原FFT结果一样点数的参考信号数组。
  3. 将原FFT结果与获得的参考信号数组做差，即可实现扣点操作。

下面是实现扣点的一种C实现，代码中中文注释帮助您更好的理解整个扣点的过程，代码能够实现对同一FFT结果进行多次的最大值扣点，可以看出代码将FFT结果剩余的所有频点的能量均值乘以一个系数作为阈值，筛选了当前所选取的最大点是否能代表当前目标的某一维度（一般为角度）信息：

void simpleDPK(STRUCT_DPKRST *Sresult,STRUCT_DPKCFG *dpkCfg, float *din,float *dinabs)
{
	float maxVal[2]={0.0};
	
	uint16_t maxIdx = 0;
	uint16_t maxIdx_left0 = 0;
	uint16_t maxIdx_right0 = 0;
	uint8_t Offset = 0;
	uint8_t dpkTime=dpkCfg->dpkTime;
	uint8_t thres=dpkCfg->thres;
	uint8_t sincLen=dpkCfg->sincLen;
	uint8_t sNumANT=dpkCfg->numAnt;
	float scalePow=1.0/sincLen;
	float sRes[12] = {0.0}; //默认扣最大12次
	Sresult->targetNum=0;
	arm_cmplx_mag_f32(din,dinabs, sincLen); //先做1次abs
	for(uint8_t k=0;k<dpkTime*3;k=k+3)  //扣点次数
	{	
		for(uint32_t j=1;j<sincLen;j++)			//拿到dinabs最大值及索引
		{
			if(dinabs[maxIdx]<dinabs[j])//拿到最大值，index是对应索引
			{
				maxIdx = j;
			}					
		}		
		maxVal[0] = din[maxIdx*2];		//拿最大实部
		maxVal[1] = din[maxIdx*2+1];	//拿最大虚部

		maxVal[0] = din[maxIdx*2];		//拿最大实部
		maxVal[1] = din[maxIdx*2+1];	//拿最大虚部
		//取左右两边索引值
		if (maxIdx == 0){
			maxIdx_left0 = sincLen-1;
			maxIdx_right0 = maxIdx+1;
		}
		else if (maxIdx == sincLen-1){
			maxIdx_left0 = maxIdx-1;
			maxIdx_right0 = 0;					
		}
		else {
			maxIdx_left0 = maxIdx-1;
			maxIdx_right0 = maxIdx+1;	
		}	
		for(uint8_t im=0;im<sincLen;im++) 
		{
			Offset=im+sincLen-maxIdx;	//拿移位索引
	  	if(Offset>=sincLen)
  		{
  			Offset=Offset-sincLen; 
			}			
	   	SincSeq[im][0]= SincBuf[Offset][0]*maxVal[0]-SincBuf[Offset][1]*maxVal[1];
	   	SincSeq[im][1] = SincBuf[Offset][1]*maxVal[0]+SincBuf[Offset][0]*maxVal[1];
	   	din[im*2]=din[im*2]-SincSeq[im][0];
	   	din[im*2+1]=din[im*2+1]-SincSeq[im][1];
			
		}
		Sresult->idx[k]=maxIdx;   //先存最大目标索引
		Sresult->pow[k]=dinabs[maxIdx];  //先存最大目标能量值		

		Sresult->idx[k+1]=maxIdx_left0;   //先存最大目标索引
		Sresult->pow[k+1]=dinabs[maxIdx_left0];  //先存最大目标能量值				
		Sresult->idx[k+2]=maxIdx_right0;   //先存最大目标索引
		Sresult->pow[k+2]=dinabs[maxIdx_right0];  //先存最大目标能量值		

		
		arm_cmplx_mag_f32(din,dinabs, sincLen); //拿到ABS值
		sRes[k] = 0.0;
		for(uint8_t im=0;im<sincLen;im++) 
		{
			sRes[k]=sRes[k]+dinabs[im];
		}
		sRes[k+1]=sRes[k];
		sRes[k+2]=sRes[k];
//		printf("k=%d, idx = %d, pow = %f, sRes = %f\r\n",k,Sresult->idx[k],Sresult->pow[k],sRes[k]);
	}
	for(uint8_t k=0;k<dpkTime*3;k=k+3){
		if(Sresult->pow[k] > sRes[0]/sincLen/(sNumANT-dpkTime) * sNumANT * thres){
			
			if (Sresult->pow[k] > 1500000) {
				for (uint8_t kk=k;kk<(k+3);kk++){
				Sresult->pow[Sresult->targetNum] = Sresult->pow[kk] /(sRes[kk]/sincLen/(sNumANT-dpkTime) * sNumANT );
		//		printf("case1: kk = %d, itargetNum=%d, snr = %f\r\n",kk, Sresult->targetNum,Sresult->pow[Sresult->targetNum]);	
				Sresult->targetNum=Sresult->targetNum+1;
				}
			}
			
			else{
				Sresult->pow[k] = Sresult->pow[k] /(sRes[dpkTime-1]/sincLen/(sNumANT-dpkTime) * sNumANT );
		//		printf("case2: kk = 1, itargetNum=%d, snr = %f\r\n", Sresult->targetNum,Sresult->pow[Sresult->targetNum]);	
				Sresult->targetNum=Sresult->targetNum+1;
			}
		}
	}
}

十六宿舍 原创作品，转载必须标注原文链接。

©2023 Yang Li. All rights reserved.

欢迎关注 『十六宿舍』，大家喜欢的话，给个👍，更多关于嵌入式相关技术的内容持续更新中。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/949461.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

文件修改时间能改吗？怎么改？

文件修改时间能改吗？怎么改？

文件修改时间能改吗&#xff1f;怎么改&#xff1f;修改时间是每个电脑文件具备的一个属性&#xff0c;它代表了这个电脑文件最后一次的修改时间&#xff0c;是电脑系统自动赋予文件的&#xff0c;相信大家都应该知道。我们右击鼠标某个文件&#xff0c;然后点击弹出菜单里面的…
阅读更多...
并发编程(四大函数接口) 06 详细讲解

并发编程(四大函数接口) 06 详细讲解

四大函数接口 函数接口&#xff1a;接口中只有一个方法 Function Function函数型接口&#xff0c;有一个输入参数&#xff0c;有一个输出只要是函数型接口可以用Lambda表达式简化 函数函数型接口&#xff0c;有一个输入参数&#xff0c;有一个输出只要是函数型接口可以用lamb…
阅读更多...
并发容器11

并发容器11

一 JDK 提供的并发容器总结 JDK 提供的这些容器大部分在 java.util.concurrent 包中。 ConcurrentHashMap: 线程安全的 HashMap CopyOnWriteArrayList: 线程安全的 List&#xff0c;在读多写少的场合性能非常好&#xff0c;远远好于 Vector. ConcurrentLinkedQueue: 高效的并…
阅读更多...
element 级联选择框偏移

element 级联选择框偏移

如图所示&#xff0c;选择之后&#xff0c;位置跑到了左上角 添加:append-to-body"false",在弹出框的定位出现问题时&#xff0c;可将该属性设置为 false
阅读更多...
（第六天）初识Spring框架-SSM框架的学习与应用(Spring + Spring MVC + MyBatis)-Java EE企业级应用开发学习记录

（第六天）初识Spring框架-SSM框架的学习与应用(Spring + Spring MVC + MyBatis)-Java EE企业级应用开发学习记录

SSM框架的学习与应用(Spring Spring MVC MyBatis)-Java EE企业级应用开发学习记录&#xff08;第六天&#xff09;初识Spring框架 ​ 昨天我们已经把Mybatis框架的基本知识全部学完&#xff0c;内容有Mybatis是一个半自动化的持久层ORM框架&#xff0c;深入学习编写动态SQL&a…
阅读更多...
淘宝京东1688商品价格监控（电商价格监测API接口系列）

淘宝京东1688商品价格监控（电商价格监测API接口系列）

淘宝价格监控&#xff0c;电商价格监测软件目前市面有一款是最火的&#xff0c;针对各个平台都可以进行价格监测&#xff0c;很多实用功能&#xff0c;今天我们就来介绍一下品牌卫士这款价格24小时监测软件都有哪些功能。 一&#xff0c;覆盖全网全平台 天猫淘宝、闲鱼、京东、…
阅读更多...
RK3588平台驱动调试篇 [ GPIO篇 ] - RK3588-对GPIO的操作控制

RK3588平台驱动调试篇 [ GPIO篇 ] - RK3588-对GPIO的操作控制

1. 简介 RK3588从入门到精通本⽂介绍Linux操作gpio⽅法开发板&#xff1a;ArmSoM-W3 2. GPIO配置 Rockchip Pin的ID按照 控制器(bank)端口(port)索引序号(pin) 组成 2.1 GPIO驱动介绍 驱动包括Pinctrl驱动&#xff08; drivers/pinctrl/pinctrl-rockchip.c &#xff09; 和…
阅读更多...
servlet初体验之环境搭建！！！

servlet初体验之环境搭建！！！

我们需要用到tomcat服务器&#xff0c;咩有下载的小伙伴看过来&#xff1a;如何正确下载tomcat&#xff1f;&#xff1f;&#xff1f;_明天更新的博客-CSDN博客 1. 创建普通的Java项目&#xff0c;并在项目中创建libs目录存放第三方的jar包。 建立普通项目 创建libs目录存放第三…
阅读更多...
2023_Spark_实验三：基于IDEA开发Scala例子

2023_Spark_实验三：基于IDEA开发Scala例子

一、创建一个空项目&#xff0c;作为整个项目的基本框架 二、创建SparkStudy模块&#xff0c;用于学习基本的Spark基础 三、创建项目结构 1、在SparkStudy模块下的pom.xml文件中加入对应的依赖&#xff0c;并等待依赖包下载完毕。 在pom.xml文件中加入对应的依赖 ​<!-- S…
阅读更多...
模拟4~20ma电流输出的设计

模拟4~20ma电流输出的设计

文章目录 1. 原理2. 使用GP8102S或GP8212S进行设计2.1 共地型设计2.2 共源型设计2.3 其它电流需求 3. 隔离光耦电源连接方案4. 利用GP8102S实现0-40V 的可编程电压输出 1. 原理 4 ~ 20ma电流输出的目的不用多说&#xff0c;今天就简单聊一下4 ~ 20ma电流输出是怎么设计出来的&…
阅读更多...
【AI】数学基础——概率论

【AI】数学基础——概率论

随着联结主义学派的兴起&#xff0c;概率统计已经取代了数理逻辑&#xff0c;成为了人工智能研究的主流工具 数理统计的关注点是 无处不在的可能性 对随机事件发生的可能性进行规范的数学描述是概率论的公理化过程 频率学派认为先验分布式固定的&#xff0c;模型参数靠最大似…
阅读更多...
C++day6

C++day6

1. #include <iostream>using namespace std; class Animal { private:int id; public:Animal(){}Animal(int id):id(id){}virtual void show(){cout << "动物园门牌号:" << id << endl;} }; class Houzi:public Animal { private:string n…
阅读更多...
用变压器实现德-英语言翻译【02/8】: 位置编码

用变压器实现德-英语言翻译【02/8】: 位置编码

一、说明 本文是“用变压器实现德-英语言翻译”系列的第二篇。它从头开始引入位置编码。然后&#xff0c;它解释了 PyTorch 如何实现位置编码。接下来是变压器实现。 二、技术背景 位置编码用于为序列中的每个标记或单词提供相对位置。阅读句子时&#xff0c;每个单词都依赖于它…
阅读更多...
日本核污染水排海，有必要囤盐吗？

日本核污染水排海，有必要囤盐吗？

据央视新闻24日报道&#xff0c;当地时间8月24日13时&#xff0c;日本福岛第一核电站启动污水排海。消息一出&#xff0c;全球哗然。虽然事情已经过去了几天&#xff0c;但是&#xff0c;随着这一举动&#xff0c;大家就乱了阵脚&#xff0c;恐惧者有之&#xff0c;辱骂者有之&…
阅读更多...
Nginx从入门到精通(超级详细)

Nginx从入门到精通(超级详细)

文章目录 一、什么是Nginx1、正向代理2、反向代理3、负载均衡4、动静分离 二、centos7环境安装Nginx1、安装依赖2、下载安装包3、安装4、启动5、停止 三、Nginx核心基础知识1、nginx核心目录2、常用命令3、默认配置文件讲解4、Nginx虚拟主机-搭建前端静态服务器5、使用nignx搭建…
阅读更多...
超声波俱乐部分享：AI冷静期，创业者们应该做什么？

超声波俱乐部分享：AI冷静期，创业者们应该做什么？

8月26日&#xff0c;2023年第十一期超声波俱乐部内部分享会在北京望京举行。本期的主题是&#xff1a;AI冷静期&#xff0c;创业者们应该做什么&#xff1f; 到场的嘉宾有&#xff1a; 超声波创始人杨子超&#xff0c;超声波联合创始人、和牛商业创始人刘思雨&#xff0c;中国…
阅读更多...
学习c++的第6天

学习c++的第6天

#include <iostream> using namespace std; class Animal { public: virtual void perform()0; virtual ~Animal() { cout<<"Animal的析构函数"<<endl; } }; class Lion :public Animal { public : void perform() { cout<<"狮子…
阅读更多...
41、springboot 整合 FreeMarker 模版技术

41、springboot 整合 FreeMarker 模版技术

springboot 整合 FreeMarker 模版技术 ★ 整合FreeMarker的自动配置&#xff1a; FreeMarkerAutoConfiguration&#xff1a;负责整合Spring容器和获取FreeMarkerProperties加载的配置信息。FreeMarkerServletWebConfiguration/FreeMarkerReactiveWebConfiguration&#xff1a…
阅读更多...
C++ 多级继承

C++ 多级继承

所谓多级继承就是代代相传&#xff0c;几代人&#xff0c;后代继承祖辈的数据和方法。但是有三种不同的继承方式而已。 构造顺序&#xff0c;即基类先构造&#xff0c;其次代代相传&#xff0c;析构顺序则是从子代先析构&#xff0c;最后析构祖先。 构造:从祖宗开始&#xff0…
阅读更多...
马上金九银十了，给大家一点面试方面的建议

马上金九银十了，给大家一点面试方面的建议

哈喽大家好啊&#xff0c;我是Hydra。 好久不见&#xff0c;甚是想念。这段时间没有更新什么文章&#xff0c;其实是因为我跳了一波槽&#xff0c;出去面了一圈后&#xff0c;也顺利拿了不少架构岗位的offer。 正好马上要金九银十了&#xff0c;相信有不少小伙伴们估计也有跳…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023